1. Main points
A statistically significant slowdown in the long-term improvement in age-standardised mortality rates for England and Wales took place around the early 2010s.
This was true for England and Wales, for both sexes, and for older and younger people, with some variations in the timing and extent of the change in trend.
2. Introduction
Over the last century there has been a long-term trend in falling mortality and rising life expectancy in the UK. This is mainly attributable to a reduction in child mortality through health improvements such as childhood immunisations during the earlier part of the 20th century, followed by medical advances in diagnosis and treatment, and improved lifestyles in the older population during the later part of the 20th century (see How has life expectancy changed over time?). In the 20 years between 1991 and 2011, life expectancy at birth for females in England and Wales grew by almost four years and for males by more than five years (see National life tables, UK: 2014 to 2016).
However, since 2011 there has been a reduction in the rate of improvement. Between 2011 to 2013 and 2014 to 2016, only 26 local authorities showed any statistically significant increase in life expectancy for men, and only 17 showed any improvement for women. This compares to 203 and 128 local authorities respectively showing a significant increase in the equivalent period 10 years earlier (see Health state life expectancies, UK: 2014 to 2016). There is debate about the reasons for the recent findings and whether they represent only a “blip” in the long-term pattern of improvement or a real change of direction (see the Why have improvements in mortality slowed down? blog by The King’s Fund, which summarises the debate).
In this article our aim is to establish definitively whether there has been a statistically significant change in the decreasing trend in mortality, and if so when it occurred. To do so we analyse age-standardised mortality rates from 1990 to 2017 using segmented regression, a technique that detects the presence of a significant change in trend (breakpoint) in a time series. The breakpoint signifies that the trends before and after it are different. We do not consider the reasons for any possible change in this report. We also do not forecast the direction the trend may take in the future.
Back to table of contents3. Things you need to know about this release
The analysis in this article was conducted using quarterly rolling annual data from the period Quarter 1 to Quarter 4 (January to December) 1990 to Quarter 1 to Quarter 4 2017. Each data point corresponds to a 12-month period and is one quarter (three months) on from the preceding data point. For example, while Quarter 1 to Quarter 4 1990 encompasses January to December 1990, the next data point Quarter 2 (Apr to June) 1990 to Quarter 1 1991 encompasses April 1990 to March 1991. This means that each data point overlaps with its two adjacent data points by nine months each, so the points are not independent from one another in the data they contain. This approach was adopted to ensure sufficient data points are available to be able to fit linear models to the time series.
The overlapping data points also mean that the trend over time is smoother than if independent annual data points had been used, reducing the impact of any short-term fluctuations. A breakpoint found in a smoothed series is stronger evidence of a substantive change having occurred. However, the limitation of using overlapping periods is the increase in the confidence intervals around the breakpoints making it more difficult to state exactly when the significant change occurred.
Back to table of contents4. What is the issue?
Almost since the first life tables were calculated in the mid-19th century, and certainly for most of the 20th century, mortality rates have shown a steady decline. This pattern continued into the first decade of the 21st century, a decade characterised by substantial and significant reductions in mortality. However, several recent reports have suggested a marked slowing in the rate of mortality improvement during the 2010s. The pattern of age-standardised mortality since the beginning of the 2010s has mostly remained stable, notwithstanding a significant fall observed in 2014, followed by a significant increase in 2015.
We have reported these trends for England in an ongoing series of quarterly mortality surveillance reports that use provisional mortality data for England for the most recent year. The changing trends in mortality are also reflected in trends in life expectancy (see our latest health state life expectancies and national life tables releases), as mortality rates are used in the calculation of life expectancy.
There has been wide interest in recent mortality patterns, particularly following analyses of 2015 deaths, which produced a statistically significant rise in mortality rates and a consequential fall in life expectancy in England between 2014 and 2015. A number of influential organisations and academics have provided commentary and analysis on these trends, including the Institute and Faculty of Actuaries and their continuous mortality investigation, and there is accompanying industry commentary on this: think tanks such as the King’s Fund; academics such as Sir Michael Marmot; as well as public bodies such as Public Health England and Public Health Wales.
There has understandably been speculation about the reasons behind the observed patterns. Some researchers have pointed to the presence of more virulent strains of influenza affecting the more vulnerable older populations. However, this is contested as a long-term effect as varying predominant strains of influenza will only explain short-term fluctuations in mortality rates, not longer-term changes in trends (see Rise in mortality in England and Wales in first seven weeks of 2018).
Several authors suggest austerity as the primary underlying cause of more recent mortality patterns, citing statistical associations with measures of healthcare performance and the worsening financial performance of NHS bodies, together with social care access constraints, as discussed in Effects of health and social care spending constraints on mortality in England: a time trend analysis. On the other hand, others have argued that such analysis does not demonstrate causal links.
A third approach attributes the trends to cohort effects, specifically higher prevalence of co-morbidity among the elderly. The risk of multi-morbidity with increasing age is found across European countries, and the higher concentrations of older people in modern economies present challenges for health and social care systems.
In this analysis we test whether the trend in mortality rates has changed significantly and give an indicative time period in which any change arose, from which explanations can then be explored. We describe analyses that formally test whether there has been a significant change in the rate of mortality improvement in recent years, using data for the period 1990 to 2017. The statistical method chosen is an objective test that does not depend on any prior assumptions about the likely date of a change in the trend. This analysis does not look at causes for any changes.
Back to table of contents5. Methods
Data used
Age-standardised mortality rates using the 2013 European Standard Population (2013 ESP) were calculated for quarterly rolling 12-month periods from Quarter 1 to Quarter 4 (January to December) 1990 to Quarter 1 to Quarter 4 2017. Age-standardisation adjusts mortality rates for changes in the age-structure of populations allowing for valid comparisons over time.
Mortality rates were calculated for both males and females, for England and Wales separately, for all ages, those aged under 75 years and those aged 75 years and over. This generated 12 different breakdowns of the data.
Analysis method
We first looked at the observed trend in age-standardised mortality rates in England and Wales for males and females.
We then used a segmented linear regression method to assess whether there has been a change in the trend in mortality rates and if so at what point in the time series it moves away from the previous trend trajectory.
Segmented linear regression fits multiple linear regression models to a series of continuous data points to determine a trend using a segmented or broken line of best fit. The point at which one segment meets the next is called a breakpoint and indicates the point of a change in trend where the difference in the coefficients of the slopes before and after the breakpoint is statistically significant.
As shown in Figure 1, the orange line is a single linear regression model produced to fit all the data (blue dots). The green line is a segmented regression model produced to fit the data assuming there is one breakpoint in the data. Overall, the green line fits the data much better than the orange line with many more blue data points being closer to the green line than the orange line. The dashed black line shows where the change in trend (breakpoint) occurred. The exact position of this breakpoint does not precisely locate any source of change, but can be used to see whether there is consistency across different countries, sexes and age groups about where the change in trend occurred in the time series.
Figure 1: Example of a segmented regression analysis
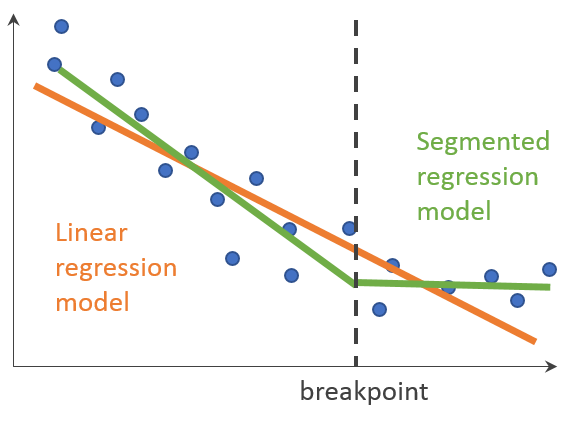
Source: Office for National Statistics
Download this image Figure 1: Example of a segmented regression analysis
.png (28.5 kB)For more information about the segmented regression analysis and how it was implemented, see the Quality and methodology section.
The segmented linear regressions were initially set to identify one breakpoint in each of the 12 breakdowns of the data. Confidence interval width was used to guide whether the trend was better represented with two breakpoints.
Back to table of contents6. Results
Observed age-standardised mortality rates in England and Wales declined from 1990 to 2017
Figure 2 shows the trend in age-standardised quarterly rolling annual mortality rates for all ages, for males and females in England and Wales separately, starting with period Quarter 1 to Quarter 4 (January to December) 1990 and ending with the same period in 2017.
In both countries and for both sexes, significant improvements in mortality rates occurred over this 27-year period, with rates substantially lower in 2017 than they were in 1990. However, the magnitude of improvement differs over time.
Figure 2: Age-standardised quarterly rolling annual mortality rates, by sex for all ages, England and Wales, 1990 to 2017
Source: Office for National Statistics
Notes:
Age-standardised mortality rates per 100,000 population, standardised to the 2013 European Standard Population.
Figures exclude non-residents, based on boundaries as of February 2018.
Q1 refers to annual period ending Quarter 1 (April to March), Q2 refers to annual period ending Quarter 2 (July to June), Q3 refers to annual period ending Quarter 3 (October to September), Q4 refers to annual period ending Quarter 4 (January to December).
Download this chart Figure 2: Age-standardised quarterly rolling annual mortality rates, by sex for all ages, England and Wales, 1990 to 2017
Image .csv .xlsFor males in England, the age-standardised mortality rate was 40.5% lower in 2017 than it was in 1990. On average over all these rolling periods, there were approximately 7.0 fewer deaths per 100,000 males for each rolling period. However, between 1990 and 2011, there were 8.6 fewer deaths per 100,000 males for each rolling period; between 2011 and 2017 this had fallen to 1.3 fewer deaths per 100,000 males, a clear weakening of 85% in the rate of improvement.
For females in England, the rate was 30.5% lower in 2017 than it was in 1990. On average over all these rolling periods, there were approximately 3.4 fewer deaths per 100,000 females for each rolling period. However, between 1990 and 2011, the improvement rate was 4.3 fewer deaths per 100,000 females for each rolling period, whereas between 2011 and 2017, it was only 0.2 deaths per 100,000 females, a 95% weakening in the rate of improvement.
For males in Wales, the age-standardised mortality rate was 37.2% lower in 2017 than it was in 1990. On average over all these rolling periods, there were approximately 6.6 fewer deaths per 100,000 males for each rolling period. However, between 1990 and 2011, there were 8.1 fewer deaths per 100,000 males for each rolling period; but between 2011 and 2017, this had fallen to 1.2 fewer deaths per 100,000 males, a weakening in the rate of improvement of 85%.
For females in Wales, the age-standardised mortality rate was 25.9% lower in 2017 than it was in 1990. On average over all these rolling periods, there were approximately 2.9 fewer deaths per 100,000 females for each rolling period. However, between 1990 and 2011, there were 3.9 fewer deaths per 100,000 females for each rolling period; between 2011 and 2017 this had changed to 0.6 more deaths per 100,000 females, and thus no improvement.
These changes are consistent with a greater rate of improvement between 1990 and 2011 than is observed since 2011, illustrating a slowing-down in improvement during the 2010s. They also show that the changes in the rate of improvement are of similar magnitude for males in England and males and females in Wales. Females in England saw their rate of improvement decline by 95% during 2011 and 2017, a sharp contrast to the previous two decades. We now use regression models to determine the timing of changes.
England
A significant slowdown in improvement in mortality rates occurred during the early 2010s in England
This section describes the results of the segmented regression analyses. Table 1 shows the breakpoints detected by the segmented linear regression function for age-standardised mortality rates in England. A statistically significant breakpoint was detected in the early part of the 2010s for all breakdowns apart from females aged 75 years and over. With this exception, the breakpoints vary in time from period Quarter 2 2009 to Quarter 1 2010 (April 2009 to March 2010) to period Quarter 2 2013 to Quarter 1 2014 (April 2013 to March 2014).
The segmented regression analyses were conducted on each breakdown independently, so breakpoints for the all ages breakdown do not have to fall between those detected for the aged under 75 years and the aged 75 years and over.
For females aged 75 years and over a breakpoint was identified at period Quarter 2 1998 to Quarter 1 1999 (April 1998 to March 1999). The confidence interval around this breakpoint is much wider than the other breakpoints, suggesting a high level of variability around the detection of this breakpoint. This initial analysis only allowed for the detection of one breakpoint. The “Analysis using two breakpoints” section provides more information about this breakdown when two breakpoints were requested for detection.
Table 1: Breakpoints indicating change in trend in age-standardised mortality rates for all ages, those aged under 75 years and those aged 75 years and over, by sex, England, 1990 to 2017
| Age | Sex | Breakpoint | Lower 95% confidence limit | Upper 95% confidence limit |
|---|---|---|---|---|
| All ages | Males | Q2 2011 to Q1 2012 | Q3 2010 to Q2 2011 | Q1 2012 to Q4 2012 |
| All ages | Females | Q2 2013 to Q1 2014 | Q1 2012 to Q4 2012 | Q3 2014 to Q2 2015 |
| 0 to 74 years | Males | Q2 2009 to Q1 2010 | Q1 2009 to Q4 2009 | Q4 2009 to Q3 2010 |
| 0 to 74 years | Females | Q2 2011 to Q1 2012 | Q3 2010 to Q2 2011 | Q4 2011 to Q3 2012 |
| 75 years and over | Males | Q3 2011 to Q2 2012 | Q3 2010 to Q2 2011 | Q3 2012 to Q2 2013 |
| 75 years and over | Females | Q2 1998 to Q1 1999 | Q2 1995 to Q1 1996 | Q2 2001 to Q1 2002 |
| Source: Office for National Statistics | ||||
| Notes: | ||||
| 1. The lower and upper 95% confidence limits have been provided. These form a confidence interval, which is a measure of the statistical precision of an estimate and shows the range of uncertainty around the estimated figure. Calculations based on small numbers of events are often subject to random fluctuations. As a general rule, if the confidence interval around one figure overlaps with the interval around another, we cannot say with certainty that there is more than a chance difference between the two figures. | ||||
| 2. Q1 refers to Quarter 1 (1 January to 31 March), Q2 refers to Quarter 2 (1 April to 30 June), Q3 refers to Quarter 3 (1 July to 30 September), Q4 refers to Quarter 4 (1 October to 31 December). | ||||
Download this table Table 1: Breakpoints indicating change in trend in age-standardised mortality rates for all ages, those aged under 75 years and those aged 75 years and over, by sex, England, 1990 to 2017
.xls (38.4 kB)Figure 3 displays the observed all ages age-standardised mortality rate over time for England by sex; the fitted trendline up until the breakpoint and an extenstion of this beyond the breakpoint to the end of the series; and the fitted segmented function indicating the trend after the breakpoint. The breakpoints are indicated by vertical plot lines. For males the breakpoint is at period Quarter 2 2011 to Quarter 1 2012 (April 2011 to March 2012) and for females it is later in the time series at period Quarter 2 2013 to Quarter 1 2014 (April 2013 to March 2014).
Figure 3: Age-standardised quarterly rolling annual mortality rates and fitted segmented model, by sex for all ages, England, 1990 to 2017
Source: Office for National Statistics
Notes:
Age-standardised mortality rates per 100,000 population, standardised to the 2013 European Standard Population.
Figures exclude non-residents, based on boundaries as of February 2018.
Q1 refers to annual period ending Quarter 1 (April to March), Q2 refers to annual period ending Quarter 2 (July to June), Q3 refers to annual period ending Quarter 3 (October to September), Q4 refers to annual period ending Quarter 4 (January to December).
Segmented model is the segmented linear regression model produced by our program to best fit the data.
Pre-breakpoint trend projected is the trend fitted to the data up until the breakpoint projected forward to the end of the observed data time series.
Download this chart Figure 3: Age-standardised quarterly rolling annual mortality rates and fitted segmented model, by sex for all ages, England, 1990 to 2017
Image .csv .xlsThe projection of the pre-breakpoint trend forward to 2017 illustrates possible mortality rates if the rate of improvement prior to the early 2010s had continued. The comparison between this projection, the observed rates and the segmented regression model fitted to the data after the breakpoint, demonstrates how the rate of improvement has slowed in recent years and mortality rates are higher than might have arisen if the pre-breakpoint rate of improvement had continued.
Change in trend in mortality rates observed at younger ages in England
Focusing on those aged under 75 years allows us to determine whether any overall change in trend is primarily an “old age” effect or more generic across age groups. Both males and females in the younger age group in England show a breakpoint in the time series of mortality rates in the late 2000s or early 2010s.
The breakpoints identified for this age group occur earlier in the time series than when all ages are considered. This suggests that the trend of improving mortality rates had started to tail off earlier for younger age groups.
Figure 4 shows the breakpoints indicated by vertical lines. For males this is at period Quarter 2 2009 to Quarter 1 2010 (April 2009 to March 2010) and for females it is detected later in the time series at period Quarter 2 2011 to Quarter 1 2012 (April 2011 to March 2012).
Figure 4: Age-standardised quarterly rolling annual mortality rates and fitted segmented model, by sex for those aged under 75 years, England, 1990 to 2017
Source: Office for National Statistics
Notes:
Age-standardised mortality rates per 100,000 population, standardised to the 2013 European Standard Population.
Figures exclude non-residents, based on boundaries as of February 2018.
Q1 refers to annual period ending Quarter 1 (April to March), Q2 refers to annual period ending Quarter 2 (July to June), Q3 refers to annual period ending Quarter 3 (October to September), Q4 refers to annual period ending Quarter 4 (January to December).
Segmented model is the segmented linear regression model produced by our program to best fit the data.
Pre-breakpoint trend projected is the trend fitted to the data up until the breakpoint projected forward to the end of the observed data time series.
Download this chart Figure 4: Age-standardised quarterly rolling annual mortality rates and fitted segmented model, by sex for those aged under 75 years, England, 1990 to 2017
Image .csv .xlsAs the breakpoint occurred earlier than for all ages, the divergence between the projected mortality rates if the pre-breakpoint trend had continued and the observed mortality rates is wider by the end of the time series. The trends following the breakpoints still show a downward slope, which indicates a continuing overall improvement in mortality rates; but this is shallower than that observed before the breakpoint.
The point of change in trend in mortality rates is less clear for those aged 75 years and over in England
Age-standardised mortality rates in those aged 75 years and over are higher than in younger age groups and show more abrupt changes in the rate over time in each direction, as Figure 5 demonstrates. This characteristic means the trend’s data points are more scattered around the line of best fit; therefore, the detection of change in trend using linear models is more challenging to determine. The greater undulation in rates observed in this age group is likely to be the result of several factors, including the relative vulnerability of this group to seasonal risk factors such as influenza and cold or hot weather.
For males in England aged 75 years and over, the breakpoint was detected at period Quarter 3 2011 to Quarter 2 2012 (July 2011 to June 2012) (Figure 5). This is much later than the breakpoint identified for males aged under 75 years in England, although the confidence interval is much wider. Consequently, the evidence for a breakpoint around the late 2000s or early 2010s is less clear in this older age group than for those aged under 75 years, which reflects the greater variability in age-standardised rates over time.
Figure 5: Age-standardised quarterly rolling annual mortality rates and fitted segmented model, by sex for those aged 75 years and over, England, 1990 to 2017
Source: Office for National Statistics
Notes:
Age-standardised mortality rates per 100,000 population, standardised to the 2013 European Standard Population.
Figures exclude non-residents, based on boundaries as of February 2018.
Q1 refers to annual period ending Quarter 1 (April to March), Q2 refers to annual period ending Quarter 2 (July to June), Q3 refers to annual period ending Quarter 3 (October to September), Q4 refers to annual period ending Quarter 4 (January to December).
Segmented model is the segmented linear regression model produced by our program to best fit the data.
Pre-breakpoint trend projected is the trend fitted to the data up until the breakpoint projected forward to the end of the observed data time series.
Download this chart Figure 5: Age-standardised quarterly rolling annual mortality rates and fitted segmented model, by sex for those aged 75 years and over, England, 1990 to 2017
Image .csv .xlsFor females aged 75 years and over in England, a breakpoint in the 1990s is found, but the confidence intervals are wider than for other breakdowns in England, and therefore it is more challenging to locate the timing of the change in trend. As the program detects the point at which the gradient changes, this can be a steepening as well as a flattening pattern. In Figure 5 the data for females show the identified breakpoint for this series of data was period Quarter 2 1998 to Quarter 1 1999 (April 1998 to March 1999). Here the trend before the breakpoint showed a slower rate of decline than that fitted and observed after the breakpoint. This indicates that mortality rates improved at a faster rate after the late 1990s than during the early 1990s.
However, the uncertainty around this breakpoint is relatively high where the true breakpoint could be anywhere between the periods Quarter 2 1995 to Quarter 1 1996 (April 1995 to March 1996) and Quarter 2 2001 to Quarter 1 2002 (April 2001 to March 2002) – this is a six-year window in which the breakpoint could have occurred. It also suggests the rate of improvement occurring following the breakpoint in this instance was sufficiently durable and sizable to out-weigh the stalling in improvement observed since 2010, when only one breakpoint was imposed for detection. The “Analysis using two breakpoints” section provides more information about this finding when the program could select two breakpoints for detection.
Wales
A significant slowdown in improvement in mortality rates occurred during the early 2010s for males in Wales
Table 2 shows the breakpoints detected by the segmented linear regression function for age-standardised mortality rates across all ages, those aged under 75 years and those aged 75 years and over, by sex in Wales. Like England, it shows that for most breakdowns there was a significant breakpoint detected in the early 2010s. The exceptions were females at all ages and, as in England, females aged 75 years and over. With these two exceptions, these breakpoints varied from period Quarter 1 to Quarter 4 2010 (January to December 2010) to period Quarter 3 2011 to Quarter 2 2012 (July 2011 to June 2012).
For the two exceptions, as with females aged 75 years and over in England, the confidence intervals around the breakpoints detected are much wider than the other breakpoints, suggesting a high level of variability around the identification of these breakpoints.
Table 2: Breakpoints indicating change in trend in age-standardised mortality rates for all ages, those aged under 75 years and those aged 75 years and over by sex, Wales, 1990 to 2017
| Age | Sex | Breakpoint | Lower 95% confidence limit | Upper 95% confidence limit | |
|---|---|---|---|---|---|
| All ages | Males | Q2 2011 to Q1 2012 | Q2 2010 to Q1 2011 | Q2 2012 to Q1 2013 | |
| All ages | Females | Q3 1995 to Q2 1996 | Q3 1993 to Q2 1994 | Q4 1997 to Q3 1998 | |
| 0 to 74 years | Males | Q1 2010 to Q4 2010 | Q2 2009 to Q1 2010 | Q3 2010 to Q2 2011 | |
| 0 to 74 years | Females | Q3 2011 to Q2 2012 | Q3 2010 to Q2 2011 | Q3 2012 to Q2 2013 | |
| 75 years and over | Males | Q3 2011 to Q2 2012 | Q4 2009 to Q3 2010 | Q2 2013 to Q1 2014 | |
| 75 years and over | Females | Q3 1998 to Q2 1999 | Q2 1996 to Q1 1997 | Q4 2000 to Q3 2001 | |
| Source: Office for National Statistics | |||||
| Notes: | |||||
| 1. The lower and upper 95% confidence limits have been provided. These form a confidence interval, which is a measure of the statistical precision of an estimate and shows the range of uncertainty around the estimated figure. Calculations based on small numbers of events are often subject to random fluctuations. As a general rule, if the confidence interval around one figure overlaps with the interval around another, we cannot say with certainty that there is more than a chance difference between the two figures. | |||||
| 2. Q1 refers to Quarter 1 (1 January to 31 March), Q2 refers to Quarter 2 (1 April to 30 June), Q3 refers to Quarter 3 (1 July to 30 September), Q4 refers to Quarter 4 (1 October to 31 December). | |||||
Download this table Table 2: Breakpoints indicating change in trend in age-standardised mortality rates for all ages, those aged under 75 years and those aged 75 years and over by sex, Wales, 1990 to 2017
.xls (38.9 kB)Figure 6 identifies the breakpoints for all ages mortality as vertical plot lines: for males it occurs at the period Quarter 2 2011 to Quarter 1 2012 (April 2011 to March 2012) and for females it occurs much earlier in the time series at the period Quarter 3 1995 to Quarter 2 1996 (July 1995 to June 1996).
For females, the detection of a breakpoint much earlier in the time series shows that prior to the period Quarter 3 1995 to Quarter 2 1996 (July 1995 to June 1996) there was a different, flatter trend in mortality rates compared with that observed following this point. The confidence interval around this breakpoint is relatively wide (roughly a four-year period) and is much wider than when a breakpoint is detected around the early 2010s in other breakdowns of the data, suggesting a higher level of uncertainty for this breakpoint.
Again, this analysis was conducted allowing for only one breakpoint to be detected. The “Analysis using two breakpoints” section provides more information about these breakdowns when two breakpoints could be detected.
Figure 6: Age-standardised quarterly rolling annual mortality rates and fitted segmented model, by sex for all ages, Wales, 1990 to 2017
Source: Office for National Statistics
Notes:
Age-standardised mortality rates per 100,000 population, standardised to the 2013 European Standard Population.
Figures exclude non-residents, based on boundaries as of February 2018.
Q1 refers to annual period ending Quarter 1 (April to March), Q2 refers to annual period ending Quarter 2 (July to June), Q3 refers to annual period ending Quarter 3 (October to September), Q4 refers to annual period ending Quarter 4 (January to December).
Segmented model is the segmented linear regression model produced by our program to best fit the data.
Pre-breakpoint trend projected is the trend fitted to the data up until the breakpoint projected forward to the end of the observed data time series.
Download this chart Figure 6: Age-standardised quarterly rolling annual mortality rates and fitted segmented model, by sex for all ages, Wales, 1990 to 2017
Image .csv .xlsSlowing in improvement in mortality rates observed for those aged under 75 years in Wales
Both males and females in the under 75 years age group in Wales had a breakpoint in the time series of mortality rates in the early 2010s. This is a clearer picture of each sex experiencing a change in trend in mortality rates than when all ages are considered.
Figure 7 shows the breakpoints indicated by vertical plot lines. For males the breakpoint is at the period Quarter 1 to Quarter 4 2010 (January to December 2010) and for females it is detected a little later in the time series at the period Quarter 3 2011 to Quarter 2 2012 (July 2011 to June 2012). While the change in trend is significant for both males and females, the difference in breakpoint timing between them is not significant for this age group as the confidence intervals overlap.
Figure 7: Age-standardised quarterly rolling annual mortality rates and fitted segmented model, by sex for those aged under 75 years, Wales, 1990 to 2017
Source: Office for National Statistics
Notes:
- Age-standardised mortality rates per 100,000 population, standardised to the 2013 European Standard Population.
- Figures exclude non-residents, based on boundaries as of February 2018.
Q1 refers to annual period ending Quarter 1 (April to March), Q2 refers to annual period ending Quarter 2 (July to June), Q3 refers to annual period ending Quarter 3 (October to September), Q4 refers to annual period ending Quarter 4 (January to December).
Segmented model is the segmented linear regression model produced by our program to best fit the data.
Pre-breakpoint trend projected is the trend fitted to the data up until the breakpoint projected forward to the end of the observed data time series.
Download this chart Figure 7: Age-standardised quarterly rolling annual mortality rates and fitted segmented model, by sex for those aged under 75 years, Wales, 1990 to 2017
Image .csv .xlsFor males, the breakpoint detected for those aged under 75 years was similar to that detected for all ages. However, the divergence between the projected mortality rates if the pre-breakpoint trend had continued and the observed mortality rates is wider by the end of the time series for those aged under 75 years, indicating a steeper rate of improvement existing pre-breakpoint for this age group.
The point of change in trend in mortality rate is less clear for those aged 75 years and over in Wales
As shown in England, age-standardised mortality rates in those aged 75 years and over are more uneven over time than the other age groups. Again, this means the linear model fit to the data is less good than in all ages models and those aged under 75 years. Like England, for males aged 75 years and over the breakpoint was identified at period Quarter 3 2011 to Quarter 2 2012 (July 2011 to June 2012). This is later than the breakpoint detected for males aged under 75 years in Wales and the confidence interval is much wider, showing greater uncertainty around the estimate of this breakpoint.
For females aged 75 years and over in Wales, a breakpoint in the 1990s is found, the confidence bounds are wider and it is therefore more challenging to locate the timing of the change in trend.
Figure 8 shows this breakpoint to be at period Quarter 3 1998 to Quarter 2 1999 (July 1998 to June 1999), which is similar to that detected for females at all ages in Wales. This shows that the trend before the breakpoint has a slower rate of decline than that fitted and observed after the breakpoint. Mortality rates improved at a faster rate after the late 1990s than during the early 1990s and out-weighed any flattening observed in the second decade of the 21st century.
For females, all age mortality and mortality among those aged 75 years and over, the breakpoint detected in the 1990s with wide confidence bounds provides a less certain picture of change occurring post-2010. However, as we referred to earlier, limiting the model to just one breakpoint has the potential to miss features of the 27-year trend occurring at other points. For this reason, we explore the trend further using two breakpoints.
Figure 8: Age-standardised quarterly rolling annual mortality rates and fitted segmented model, by sex for those aged 75 years and over, Wales, 1990 to 2017
Source: Office for National Statistics
Notes:
Age-standardised mortality rates per 100,000 population, standardised to the 2013 European Standard Population.
Figures exclude non-residents, based on boundaries as of February 2018.
Q1 refers to annual period ending Quarter 1 (April to March), Q2 refers to annual period ending Quarter 2 (July to June), Q3 refers to annual period ending Quarter 3 (October to September), Q4 refers to annual period ending Quarter 4 (January to December).
Segmented model is the segmented linear regression model produced by our program to best fit the data.
Pre-breakpoint trend projected is the trend fitted to the data up until the breakpoint projected forward to the end of the observed data time series.
Download this chart Figure 8: Age-standardised quarterly rolling annual mortality rates and fitted segmented model, by sex for those aged 75 years and over, Wales, 1990 to 2017
Image .csv .xlsAnalysis using two breakpoints
To further explore the time series where a breakpoint was detected around the late 1990s, we re-analysed these data by allowing the segmented regression to select two breakpoints. The reasoning for this was that these instances were inconsistent with the majority of the results, the precision was lower for these breakpoints, and the observed pattern of trend suggested the presence of more than one breakpoint. The uncertainty around the breakpoints detected in the mid or late 1990s was always higher than those detected around the late 2000s or early 2010s, suggesting that there may be more than one relevant breakpoint for these time series and one breakpoint is not sufficient to fit an adequate segmented regression model.
Allowing two breakpoints to be detected means that two breakpoints can be identified anywhere in the time series to best optimise the goodness of fit of the segmented model. This means that the breakpoint identified from the original analysis (allowing only one breakpoint) does not have to be selected by the program again in the two-breakpoint analysis.
Re-analysis of the time series where a breakpoint was originally found in the mid to late 1990s, to allow two breakpoints to be detected, showed that there was always a breakpoint in the early 2010s along with one in the late 1990s or early 2000s. This makes sense when viewing the observed trend, where strong improvements were detected in the first decade of the 21st century.
Table 3 shows these new breakpoints for the three time series that were re-analysed.
Table 3: Breakpoints indicating two points of change in trend in age-standardised mortality rates by age, sex and country, 1990 to 2017
| Country | Sex | Age range | Break point 1 | Lower 95% confidence limit | Upper 95% confidence limit | Break point 2 | Lower 95% confidence limit | Upper 95% confidence limit | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Wales | Female | All | Q3 1998 to Q2 1999 | Q3 1997 to Q2 1998 | Q4 1999 to Q3 2000 | Q1 2011 to Q4 2011 | Q1 2010 to Q4 2010 | Q1 2012 to Q4 2012 | |||||
| England | Female | 75 and over | Q1 2003 to Q4 2003 | Q3 2001 to Q2 2002 | Q3 2004 to Q2 2005 | Q4 2010 to Q3 2011 | Q4 2009 to Q3 2010 | Q4 2011 to Q3 2012 | |||||
| Wales | Female | 75 and over | Q3 2002 to Q2 2003 | Q3 2001 to Q2 2002 | Q4 2003 to Q3 2004 | Q4 2010 to Q3 2011 | Q4 2009 to Q3 2010 | Q4 2011 to Q3 2012 | |||||
| Source: Office for National Statistics | |||||||||||||
| Notes: | |||||||||||||
| 1. The lower and upper 95% confidence limits have been provided. These form a confidence interval, which is a measure of the statistical precision of an estimate and shows the range of uncertainty around the estimated figure. Calculations based on small numbers of events are often subject to random fluctuations. As a general rule, if the confidence interval around one figure overlaps with the interval around another, we cannot say with certainty that there is more than a chance difference between the two figures. | |||||||||||||
| 2. Q1 refers to Quarter 1 (1 January to 31 March), Q2 refers to Quarter 2 (1 April to 30 June), Q3 refers to Quarter 3 (1 July to 30 September), Q4 refers to Quarter 4 (1 October to 31 December). | |||||||||||||
Download this table Table 3: Breakpoints indicating two points of change in trend in age-standardised mortality rates by age, sex and country, 1990 to 2017
.xls (38.9 kB)Figure 9 shows the data for females aged 75 years and over in England again but analysed allowing for two breakpoints. The two breakpoints are now detected at the periods Quarter 1 to Quarter 4 2003 (January to December 2003) and Quarter 4 2010 to Quarter 3 2011 (October 2010 to September 2011).
Figure 9: Age-standardised quarterly rolling annual mortality rates and fitted segmented model, females, for those aged 75 years and over, England, 1990 to 2017
Source: Office for National Statistics
Notes:
Age-standardised mortality rates per 100,000 population, standardised to the 2013 European Standard Population.
Figures exclude non-residents, based on boundaries as of February 2018.
Q1 refers to annual period ending Quarter 1 (April to March), Q2 refers to annual period ending Quarter 2 (July to June), Q3 refers to annual period ending Quarter 3 (October to September), Q4 refers to annual period ending Quarter 4 (January to December).
Segmented model is the segmented linear regression model produced by our program to best fit the data.
Download this chart Figure 9: Age-standardised quarterly rolling annual mortality rates and fitted segmented model, females, for those aged 75 years and over, England, 1990 to 2017
Image .csv .xlsThis additional analysis provides further support for a change in trend in mortality rates around the late 2000s or early 2010s. It also shows, for the older ages especially, that there appears to have been a change in mortality rates in the early part of the first decade of the 21st century in England and the late 1990s in Wales, when increases in the rate of improvement in mortality rates were strong. The second breakpoint then indicates this rate of improvement slowing markedly a decade or so later.
Back to table of contents7. Conclusions
Of the 12 demographic and geographical breakdowns of age-standardised mortality rate trends examined, nine showed a clear change in mortality trend that began in the early 2010s, when only one breakpoint in the series was requested from the program’s algorithm. The other three showed a change at around the same time, but in addition to a change in the 1990s or early 2000s, when two breakpoints were requested from the program. The analysis used a smoothed time series and made no prior assumptions about the timing of the change. This provides independent evidence that there has been a significant reduction in mortality improvements compared with the durable, long-term mortality declines observed in the decades preceding 2010.
The findings were common to males and females and to those aged under 75 years and aged 75 years and over alike, suggesting that this change – whatever its cause – is not restricted to certain demographic groups but is more widespread.
This analysis did not address the differences in mortality patterns between detailed age groups, by socioeconomic factors, or for geographical areas below national level. Neither have the influence of specific causes of death, or any of the competing causal explanations, been examined at this stage. No definite inference can be made at this point on how the trends will develop in the future.
Back to table of contents8. Next steps
We are planning a series of analytical reports to explore these mortality trends in more detail, looking at age groups, geographical and socioeconomic differences, and which causes of death are instrumental in bringing about this change in trend.
In particular, we expect to look at:
the contribution of specific cause of death groupings pre- and post-breakpoint for each population breakdown
the trend in avoidable mortality by area-level deprivation over the period 2001 to 2016
the trend in life expectancy by the National Statistics Socioeconomic Classification to encompass the period 2012 to 2016
age decomposition of life expectancy and estimation of the contributions of period and cohort effects
analyses at the UK level (with agreement from the Scotland and Northern Ireland administrations) and within England
interrupted time series regression to quantify departure from trend and years lost linked to period effects
analysing longevity trends for comparable countries to the UK over the period 2001 to 2016
comparing recent trends in mortality and life expectancy between all four constituent countries of the UK
Given that most of the breakpoints were identified around the early 2010s, this pattern of reduced rates of improvement has endured for approximately seven years. While this represents a lengthy period where the rate of death has shown a marked slowdown in the rate of improvement, it is necessary to regularly review this analysis as more data points become available. New data will enable us to comment further on the direction of mortality patterns as the decade continues. This analysis doesn’t enable us to predict what will happen in the future, but the latest release of our Quarterly mortality report for England shows that the “flattening off” of mortality rates has continued.
Back to table of contents9. Quality and methodology
Data used
Data to calculate age-standardised rates for England and Wales are readily available from 1959 onwards. However, we have chosen to focus on more recent trends from 1990 to 2017, whilst not restricting the analysis to only the 21st century. This time frame ensures sufficient relevance to current trends, but gives an opportunity for breakpoints to be identified in the adjacent 1990s decade, so that patterns that are similar to or are greater than more recent mortality patterns can be identified.
Mortality rates were calculated for both males and females, for England and Wales separately, for all ages, those aged under 75 years and those aged 75 years and over. This generated 12 different breakdowns of the data. The split of age groups was used because ages up to 74 years are generally used for the measurement of premature mortality. The under 75 age group allows for analysis of trends in premature mortality over time. This analysis does not use age-specific rates.
Age-standardised rates
Deaths data for 2017 are provisional and population denominators in rate calculations for 2017 are based on population projections. Information on how age-standardised rates are produced can be found in the User guide to mortality statistics. Age-standardisation adjusts mortality rates for changes in the age-structure of populations allowing for valid comparisons over time. However, as five-year age bands are used in the standardisation process it does not account for changes within age bands. This is particularly relevant for the 90 and over age group, which encompasses a wider range of ages. The method for calculating quarterly rolling annual population estimates can be found in our Quarterly mortality report.
Segmented regression approach
We used a segmented linear regression method to assess whether there has been a statistically significant change in the trend in mortality rates, and if so at what point in the time series it moves away from the previous trend trajectory. Segmented linear regression fits multiple linear regression models to a series of continuous data to determine a trend using a segmented or broken line of best fit. The segmented model produced is continuous so that the end of one segment must meet where the next segment begins. Linear models were chosen for simplicity and provide a sufficient approximation for this analysis.
We implemented this analysis using an algorithm in the software package R, the theory of which is explained in this paper, Segmented: An R Package to Fit Regression Models With Broken-Line Relationships (Muggeo 2008). The “segmented” function in R allows users to specify the number of breakpoints they wish to find. We initially set the function to detect one breakpoint as we are testing for only one change in trend in our time series.
The breakpoints found by the segmented function are the optimal points where linear models before and after the breakpoint have a greater goodness of fit than one model for the whole series. The first breakpoint that the program finds (if only one is specified), will be the most optimal breakpoint for the whole time series. Therefore, if a breakpoint is found around a particular quarter in the time series, this would serve as evidence favouring the hypothesis that there was a change in the trend of mortality rates that started around this time.
A confidence interval around the breakpoint can also be calculated, indicating the variance and level of uncertainty around where the breakpoint is placed in the time series. The breakpoint is found using an iterative process and so the exact point found may vary each time that a model is run, depending on the data. The confidence intervals show the spread of the breakpoints from the iterations of the model.
The segmented function also contains within it a significance test called the Davies test (see Hypothesis testing when a nuisance parameter is present only under the alternatives and Hypothesis testing when a nuisance parameter is present only under the alternative: linear model case), which selects one breakpoint and returns the significance of the difference-in-slope before and after the breakpoint. This is conducted independently of the segmented function. We constrained the breakpoints identified by the segmented function to be in line with those detected by the Davies test to ensure a significant breakpoint was identified.
Back to table of contents