In this section
- Disclaimer and feedback
- Main points
- Things you need to know about this release
- Background information
- Estimation methods
- Previous simulations research
- Dual-system estimation research
- Weighting class estimation research
- Comparing DSE with WCE
- Summary and future developments
- Annex A: Equations for performance measures
- Annex B: “Active” Statistical Population Dataset methodology
1. Disclaimer and feedback
These Research Outputs are not official statistics on the population. Rather they are published merely as outputs from research into a methodology different to that currently used in the production of population statistics. These outputs must not be reproduced without this disclaimer and warning note and should not be used for policy- or decision-making.
If you have any questions or feedback, please email Admin.Data.Census.Project@ons.gov.uk (and include the subject line "Research Outputs feedback"). Many thanks.
Back to table of contents2. Main points
Following the publication of our Research Outputs on estimating the size of the population, we've investigated the use of a coverage survey to adjust the quality of administrative data population estimates for 2011.
Using census and administrative data from 2011, we've used two approaches for estimating the population: dual-system estimation (DSE) and weighting class estimation (WCE).
The DSE results reported in this paper overestimate the population of England and Wales by approximately 4%, compared with the unadjusted administrative data estimates, which underestimate by 0.1%.
While we can't measure all of the potential sources of bias in the DSE results, this overestimation is likely to be partly caused by "over-coverage" on administrative data sources – individuals that are registered at addresses that they have since moved out of.
In contrast, the WCE simulations reported in this paper underestimate the population of England and Wales by approximately 2%.
Further research is needed to understand the sources of bias in the WCE results; however, it is likely that this underestimation is partly caused by "within-household non-response" – failure to collect information on all individual members within a household that have responded to surveys (for more information, see Section 5).
Both the DSE and WCE approaches presented in this article would be improved by designing a survey that makes use of administrative data to support data collection for coverage adjustment.
We're developing and testing a Population Coverage Survey (PCS), which we aim to make fully operational by 2020 – this will be designed to address the issues identified in this article.
We continue to explore additional data sources to improve our population estimation methodology, in particular sources of "activity"1 data, which can help to confirm that individuals are usually resident in the population and in the correct location – these sources are of particular importance to support these coverage adjustment methods.
Notes for: Main points
- "Activity" can be defined as an individual interacting with an administrative system, for example, for National Insurance or tax purposes, when claiming a benefit, attending hospital or updating information on government systems in some other way.
3. Things you need to know about this release
These Research Outputs are not official statistics on the population. Rather they are published merely as outputs from research into a methodology different to that currently used in the production of population statistics.
Our methodology is based on linking administrative records to a coverage survey that has been sampled from 2011 Census data.
We've tested two estimation methods, which we use to adjust for coverage biases on our second version of a Statistical Population Dataset (SPD V2.0). These are dual-system estimation (DSE) and weighting class estimation (WCE). Each method has a set of assumptions (see Section 5), which we can't fully meet within an administrative data context. However, we're limited in the availability of more suitable alternatives. Detailed information about these methods and their application in population estimation can be found in our Beyond 2011: Estimating the population: in theory (861.2KB) article.
We use the term "households" when referring to the grouping of individual characteristics of survey responders in the WCE approach. The definition of a "household" in this research is actually based on the concept of "occupied addresses" from administrative data, which is different from traditional "household" definitions used in censuses and surveys. This definition also includes communal establishments, which aren't included in the household definitions used in censuses and surveys.
Back to table of contents4. Background information
The Administrative Data Census (ADC) Project is working to assess whether the government-stated ambition that "censuses after 2021 will be conducted using other sources of data" can be met. We're aiming to produce population estimates, household estimates and population and housing characteristics using a combination of administrative and survey data. This is to meet demands for improved population statistics and as a possible alternative to the census.
In November 2016, we released an update on our methodological developments to produce our second version of a Statistical Population Dataset (SPD V2.0)1. This explained one of our next steps was to develop an estimation framework that aims to produce unbiased estimates of the population. This article updates on our progress on this and will focus on producing coverage-adjusted population estimates using administrative data.
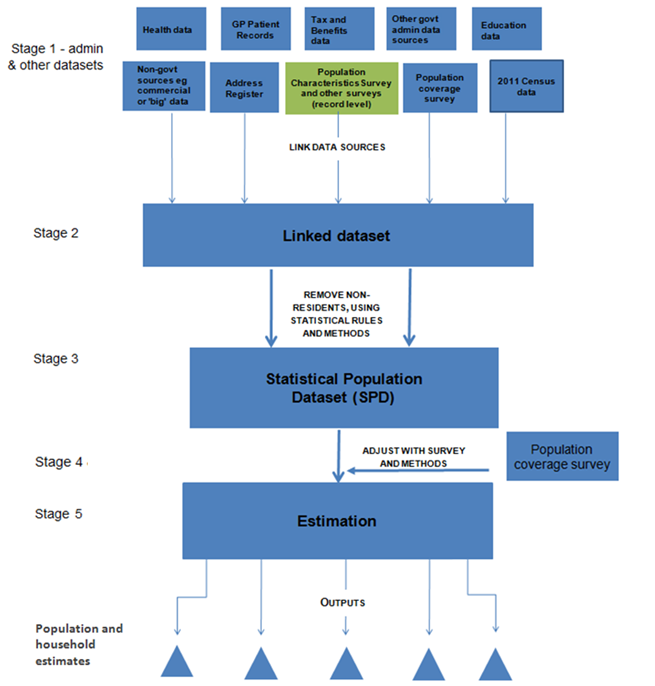
The proposed framework to achieve this is shown in Figure 1. This is similar to the framework for the 2011 Census but record-level linked administrative data (in the form of an SPD) replace the census. The stages outlined in Figure 1 are as follows:
Stage 1: Evaluate the quality and integrity of the administrative, survey and other data sources individually
Stage 2: Link data sources at record level whilst preserving privacy
Stage 3: Construct a Statistical Population Dataset (SPD) through a set of "rules" to determine which records and/or matches from the linked dataset are included in the usually resident population2
Stage 4: Carry out a Population Coverage Survey (PCS), which is designed to measure both the under- and over-coverage of the SPD
Stage 5: Produce estimates of the usually resident population by age, sex and geographical area and number of households
Figure 1: Framework for producing Administrative Data Census outputs by combining data sources
Notes:
- Health data do not include confidential medical data.
- The full framework for an Administrative Data Census is available.
Download this image Figure 1: Framework for producing Administrative Data Census outputs by combining data sources
.png (105.1 kB)In relation to stages 2 and 3, in November last year we published our latest Research Outputs estimating the size of the population for 2011 and 2016 at output area (OA) level. This demonstrated matching and methodological developments to SPD V1.0 to create our second version of an SPD (SPD V2.0). SPD V2.0 links administrative records from four datasets:
- NHS Patient Register (PR)
- Department for Work and Pensions' (DWP) Customer Information System (CIS)
- Higher Education Statistics Agency (HESA)
- school census (SC) data
For the majority of local authorities, estimates of total population size from SPD V2.0 in 2011 are similar to the 2011 Census. There are, however, larger differences between SPD V2.0 and the 2011 Census when broken down by age and sex and at lower geographies. This could be due to coverage error on the SPD, such as:
- under-coverage – a record is not included on the SPD when it should be, which results in underestimating the true population
- over-coverage – a record is included on the SPD when it shouldn't be (no longer resident in England and Wales, for example), which results in overestimating the true population
Figure 2 shows examples of different types of over-coverage prevalent on the SPD.
Figure 2: Example of erroneous inclusions and incorrect inclusions and exclusions on the Statistical Population Dataset
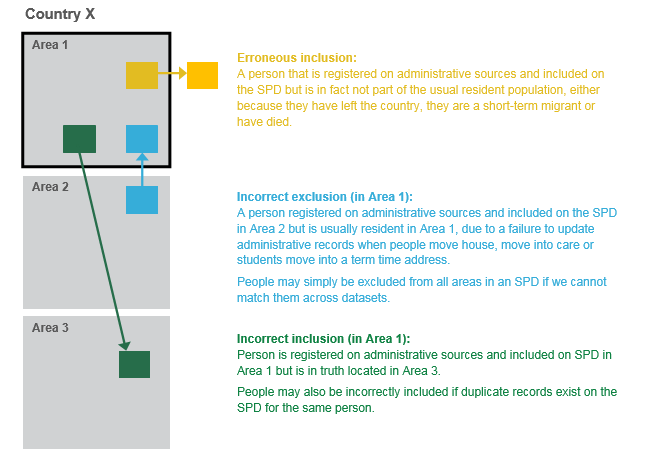
Download this image Figure 2: Example of erroneous inclusions and incorrect inclusions and exclusions on the Statistical Population Dataset
.png (30.1 kB)As outlined in stage 4 of Figure 1, a Population Coverage Survey (PCS) will be needed to produce unbiased population estimates from a future Administrative Data Census. The PCS that we plan to run annually to support the Administrative Data Census is similar to the Census Coverage Survey (CCS), which was used to produce census population estimates in 2001 and 2011.
The CCS is primarily designed as an independent data collection survey to assess and adjust for census non-response (under-coverage). However, the future PCS to support an Administrative Data Census also needs to be designed to measure and adjust for the types of over-coverage outlined in Figure 2.
We're currently exploring whether a "dependent sampling" approach is viable for collecting specific information about over-coverage. Dependent sampling in this context involves the use of administrative records to support data collection, for example, targeting areas or addresses where there is evidence that individuals have recently moved address.
In some countries, for example, in Israel where a register-based census is in operation, names of individuals registered on administrative sources at the addresses selected for the coverage survey are supplied to field interviewers before visiting the addresses. This information is used by the interviewer to check with survey respondents whether individuals on the list that haven't been captured by the survey have moved out of the address. As part of our review of international approaches, we'll be considering the potential for using dependent sampling from an ethical, legal and public acceptability perspective.
Between 2018 and 2020, we've scheduled a series of PCS tests with the aim of implementing a full-scale PCS by 2021 (see Section 10). Until this time, we don't have any survey data that has been specifically designed for use with administrative data to produce population estimates.
For the purpose of this research, we have produced coverage-adjusted estimates for 2011 by taking a sample of 2011 Census data in such a way that the sample size and spread is similar to the potential design of a future PCS that covers all local authorities. This enables us to compare our adjusted estimates with the 2011 Census population estimates and obtain an overall measure of bias. While it isn't possible to measure all the components of bias in these estimators, we can observe overall differences in the estimates produced with and without coverage adjustment.
The following sections describe how we attempt to produce population estimates using the framework described in Figure 1, focusing on stage 5 (applying estimation methods to adjust for coverage errors).
Notes for: Background information
An SPD is a single, coherent dataset that forms the basis for estimating the population. It is produced by linking records across multiple administrative data sources and applying a set of inclusion and distribution rules.
The definition of a "usually resident population" is people who reside, or intend to reside, in the country for at least 12 months, whatever their nationality. This is consistent with the standard UN definition for population estimates.
5. Estimation methods
Dual-system estimation
One of the methods we have explored to adjust our administrative data-based population estimates involves dual-system estimation (DSE). The basic capture-recapture approach of DSE is to count a sample of the population once and count a second sample (often from a follow-up survey), hence "dual-system" estimation.
Traditionally, DSE is designed to account for under-coverage in the form of non-response. This method was used in the coverage adjustment of the 2011 Census estimates. More information on this can be found in the Trout, Catfish and Roach guide (PDF, 817.2KB) to census population estimates.
In our context, the problem isn't just one of non-response and under-coverage (see cell C in Figure 3). There is also the problem of over-coverage in the administrative data (see cell B in Figure 3). Because of this, a simple capture-recapture approach is not possible. Therefore, we have adapted the traditional DSE method to account for the complexities of the administrative data (see Section 7).
Matching the Statistical Population Dataset (SPD) to the Population Coverage Survey (PCS) at record level identifies how many people are counted on both sources. This match count, along with the SPD and PCS totals, are used to adjust for non-responders in the sampled area.
Figure 3: Contingency table for the Statistical Population Dataset (SPD) and Population Coverage Survey (PCS) outcomes
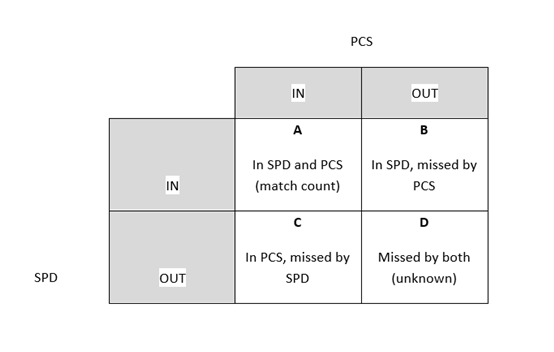
Download this image Figure 3: Contingency table for the Statistical Population Dataset (SPD) and Population Coverage Survey (PCS) outcomes
.png (17.6 kB)We can identify the counts for cells A, B and C in Figure 3. DSE allows us to estimate a total that also accounts for the people in cell D – those who weren't counted by either the SPD or the PCS.
The DSE equation for the estimated total is:
DSE has the following assumptions:
- there is perfect matching
- there should be no erroneous records on the SPD or the PCS
- the PCS is independent of the SPD
- non-response is homogenous (similar) within groups
- the population is closed (there is no immigration or emigration)
Any violation of these assumptions will result in biased population estimates using DSE. The person matching we've used to construct the SPD and link to census records is described in our Beyond 2011: Matching anonymous data (PDF 320KB) methodology article, which demonstrates that our matching method introduces approximately 1% of false links and up to 3% missed links. These matching errors will introduce proportionate levels of bias to our DSE estimates, with false links introducing a negative bias and missed links introducing a positive bias. That is to say, a 1% increase in matching error results in a 1% increase in bias. Since missed links are in greater number than false links, we expect matching error in the DSE approach to result in overestimation of population size. These missed links would occur as a result of cells B and C of Figure 3.
Additionally, over-coverage in the SPD (see Figure 2 – erroneous inclusions) also inflates the non-response adjustment and results in a positive bias in the estimate. Here, the SPD total includes records that are not part of the usually resident population and won't be matched to the PCS, but they still contribute to the DSE adjustment. These records would fall into cell B in Figure 3, where they can't be distinguished from the SPD records that are true non-responders to the PCS.
The third assumption of DSE may be an issue if survey non-response is not independent from under-coverage (due to people not being recorded in the administrative data, for example) on the SPD. This is a similar problem to that experienced with the 2011 Census. The census meets this assumption by drawing an independent sample for the Census Coverage Survey (CCS). In the administrative data context, this is less of an issue because SPD data are collected independently by other government departments, whereas the PCS will likely be a multimodal survey.
Non-response is assumed to be similar within groups. Therefore, it's important that the stratification reflects homogeneity – for example, the same age-sex group in similar geographical areas. The lower the geography level, the more likely groups will be homogenous as the variation of under- and over-coverage is reduced, although the risk of small cell sizes increases.
A hard-to-count (HtC) index was used in the designs of the 2001 and 2011 CCS to reduce the variability within groups, using prior knowledge of variability of under-coverage within local authorities. An equivalent index is likely to be required to account for this assumption of homogeneity in the context of administrative data. However, this has not yet been developed.
Weighting class estimation
An alternative estimation approach to DSE to produce coverage-adjusted population estimates is weighting class estimation (WCE). This technique weights "classes" (types) of households, or people within households, with similar propensities to respond to adjust for survey non-response (see Sampling: design and analysis (Lohr, 1999) (PDF, 7.35MB) for more information). This approach hasn't been used by Office for National Statistics (ONS) for census population estimation but has been considered in a previous assessment of the method to be a suitable coverage adjustment for the 2021 Census.
It's assumed that households with similar characteristics have a similar likelihood of responding, or not responding, to a survey. Class weights are applied to responders within classes to account for the non-responders with similar characteristics. A detailed description of the weighting approach for weighting class estimation (PDF, 861.2KB) is available.
This approach takes the count of survey responders within a class and applies an estimation weight to adjust for the non-responding households. This weight is calculated using the SPD counts for that class from households that do respond to the survey as well as the SPD counts for households that are not identified on the survey.
Weighting class example
For a given sampled area, we have two counts of the population – one from the PCS and one from the SPD. Using an address frame we can identify all households who respond to the PCS, as well as those that are counted in the SPD but not included on the PCS (the survey non-responding households). Figure 4 shows the number of individuals in a class for each household found in the PCS and SPD in a sampled area.
Figure 4: Household counts for a single class in a sampled area
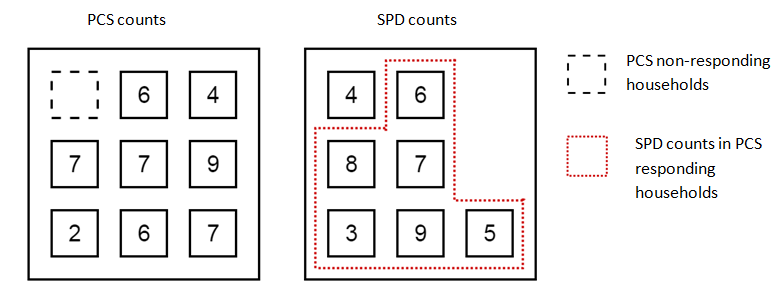
Source: Office for National Statistics
Download this image Figure 4: Household counts for a single class in a sampled area
.png (33.3 kB)In Figure 4, the total PCS class count is 48 from eight responding households. The SPD class count is 42 with counts from seven households. Of the 42 people recorded in households on the SPD, 38 of those are in households that responded to the PCS and four are in a household that didn’t respond to the survey.
The WCE adjustment takes the survey count for a class and applies the adjustment weight calculated from the SPD data using the following formula:
For this example, the class weight is calculated as follows:
We multiply this by the total survey count to calculate the coverage-adjusted estimate to be as follows:
As with DSE, there are several assumptions of WCE:
- the address frame should be of high quality
- it must be possible to match addresses to the address frame
- response propensities are homogenous (similar) within classes
- over-coverage patterns are the same for the survey responding and non-responding households
- there is no within-household non-response on the PCS
A weighting classes approach is advantageous over DSE as it's less sensitive to over-coverage and does not rely on person matching. However, it does require a high-quality address frame to enable accurate matching of households to avoid underestimation of population size. Although information about the individual characteristics of survey non-responders is required to form classes of households, this method is applied at a household level.
A violation of homogeneity of groups could lead to a positive bias in the estimates. This could counter, or indeed mask, large negative biases produced by within-household non-response. As with DSE, a hard-to-count index could help to reduce this.
The weighting methods used in a WCE approach assume that the response probabilities can be estimated for all household units. That is to say that households responding to the survey are representative of those that don't. For more information, see Sampling: design and analysis (Lohr, 1999) (PDF, 7.35MB).
A major limitation of the method is that it doesn't account for within-household non-response. This occurs when a survey response is obtained for a household for at least one resident, but another resident within that household didn't respond. This results in underestimation of the population.
Within-household non-response to the 2011 Census Coverage Survey (CCS) was estimated to be about 2.5% at national level but varies between age-sex groups and geographical locations. The DSE method used for the Census in 2011 made adequate adjustments for this. However, a weighting class estimator would not have adjusted for this error. As a consequence, we expect that our estimates will underestimate when compared with the 2011 Census estimates.
Back to table of contents6. Previous simulations research
Prior to our work, simulation studies were undertaken to compare the performance of dual-system estimation and weighting class estimation under various conditions. Two reports provide the detail relevant to our investigations:
- Beyond 2011: Producing population statistics using administrative data: in theory (PDF, 861.2KB)
- Report of results of the third phase of simulation (Castaldo et al, 2014) – this is an internal Office for National Statistics (ONS) report and is available on request
Each report explains how artificial Statistical Population Datasets (SPDs) were created and controlled levels of under- and over-coverage according to characteristics of the populations of the areas modelled. Multiple simulations were run, each drawing a different Population Coverage Survey (PCS) sample, before applying each estimator. Performance was evaluated using the following three main measures:
- relative bias (RB) – the average percentage difference from the "true" population values, with a small RB meaning that the estimate is close to our "true" population
- relative standard error (RSE) – the variability of the estimates relative to the census estimate
- relative root mean squared error (RRMSE) – a measure of the accuracy of the estimates, taking into account both RB and RSE, with a lower RRMSE value meaning a more precise estimate
The equations for these performance measures are defined in Annex A.
The main findings from the two research papers are summarised in this section.
DSE produced the most biased estimates when there was over-coverage in administrative records. However, it was shown that an SPD designed to minimise over-coverage would likely produce improved estimates.
It had been found in previous research that using age-sex (direct) classes was the best WCE alternative to DSE. Simulations show that direct-WCE only out-performs DSE when there is no within-household non-response (see Section 5). It was also shown that, unlike DSE, WCE bias remains stable under various levels of over-coverage.
All simulations assume perfect matching between the PCS and SPD and that the SPD contains no erroneous inclusions. Since these simulations were performed, ONS has obtained access to some sources of "activity" data to help identify erroneous records that can be removed from the SPD. Additionally, we now use Unique Property Reference Numbers (UPRNs) with high coverage of addresses, improving our address matching for the purposes of WCE.
Back to table of contents7. Dual-system estimation research
This section will outline how we’ve applied the principles of dual-system estimation (DSE) to our 2011 Statistical Population Dataset (SPD) data, to produce coverage-adjusted population estimates.
How have we applied DSE to our SPD? To apply DSE, we need to link the Population Coverage Survey (PCS) and the SPD. To do this, we apply our deterministic matching methodology using match keys (PDF, 320KB) to link records with a Patient Register (PR) or Customer Information System (CIS) source link in SPD V2.0 2011 to 2011 Census data (from which we draw a PCS sample). Although SPD V2.0 also includes links from Higher Education Statistics Agency (HESA) and school census (SC) data, all links in the SPD have either a PR or CIS link, or links from both these data sources. To minimise the conflicts in the matching of census data to the SPD, only PR and CIS to census links are made.
In the 2011 Census coverage adjustment, the Census Coverage Survey (CCS) was a 1% sample of households in England and Wales. We anticipate that the PCS will be a similar sample size, unless we are able to additionally measure over-coverage through dependent sampling. If we can carry out dependent sampling, the sample size would increase. To draw a 1% PCS sample from census data, 4% of Primary Sample Units (PSUs) are randomly selected – from which 25% of Secondary Sampling Units (SSUs) are then sampled. These are sampled from a geographical sampling frame.
In this research, we sample output areas (OAs) as SSUs. These are sampled from PSUs at middle layer super output area (MSOA) level. However, this may not be the approach we take when we run our PCS. An update on our developments of the PCS will be released later this year.
This sampling method can provide a desirable sample size for a PCS. To reduce sampling error, we can draw multiple samples. Given that multiple samples can be drawn from the 2011 Census, repeating this sample approach 100 times and averaging out the estimates at local authority, age and sex groups allows us to have a measure of variance. For a future PCS, we would need to apply a similar bootstrapping methodology as used for the 2011 Census population estimates to obtain measures of variance (PDF, 139.6KB).
Sampling weights for PSUs and SSUs are calculated as the inverse of the probability of an area being selected. For the 1% sampling method outlined previously, the sampling fraction for a PSU is 4%. Therefore, the sampling weight for a PSU is calculated as:
The PSU and SSU sampling weights are multiplied to obtain an overall sampling weight. Every PCS estimate for a sampled area is multiplied by this sampling weight to represent the population size of that area.
To adjust for non-response, the PCS and SPD populations are stratified by MSOA and five-year age and sex groups in the sampled areas. By stratifying at MSOA level, we generally meet the assumption that matched cell sizes are greater than seven (see cell A of Figure 3). Our research found that stratifying by lower geographies results in lower cell sizes, which can introduce biases to our estimates. We also aggregate individuals aged 80 and over to account for this assumption. However, other biases may be introduced as we could lose homogeneity within these groups by aggregating records.
Counts for these groups in the SPD and PCS are compared to identify survey non-responders. In the context of a census, linkage to the coverage survey would be a suitable way of identifying survey non-responders. However, a limitation to applying this method using administrative data is that, due to over-coverage on the SPD, we may also be identifying erroneous SPD records. It is assumed that similar levels of under-coverage occur within each stratum.
As mentioned in Section 5, a hard-to-count (HtC) index could be used to improve our ability to meet this assumption. However, further research is required to develop an administrative data equivalent. The DSE survey non-response weight is applied to the PCS counts in these strata to adjust for under-coverage.
An overcount weight is then applied to the adjusted survey estimates to adjust for over-coverage (see Estimating and correcting for over-count in the 2011 Census). The weight is applied at regional level, using Government Office Region (GOR) classifications, to account for small counts of incorrect inclusions within OAs. This reduces the inflationary effect of the DSE non-response weight to correct for over-coverage in areas where an individual is recorded in the SPD in an area which they are not truly usually resident. This "true" area of usual residency is provided by the PCS as it is assumed that this is more recent and, particularly with the presence of a face-to-face interview data collection method to confirm residents of an address, is more accurate. The overcount weight should always be less than or equal to one to reduce the estimate from the previous non-response adjustment.
A ratio weight is applied at local authority, age and sex level once these adjustments have been made. This is to reduce the variance and provide final estimates for the desired total population of England and Wales. Ideally, we would apply the ratio weight at estimation area, age and sex level, incorporating a hard-to-count index, as with census. However, as we focus mainly on results at a national level in this report we don't expect that the variability of our estimates will be affected greatly. A detailed description of the weighting approach for DSE (PDF, 861.2KB) is available.
These final estimates are averaged out over the 100 simulated PCS samples to produce coverage-adjusted estimates at local authority and five-year age and sex level. The analysis of these outputs is described in the following section.
Results of DSE simulation using SPD V2.0
Our first application of DSE was based on adjusting SPD V2.0 population estimates for 2011. This was prior to any attempt at removing erroneous records from the SPD using sources of activity data. SPD V2.0 is very likely to contain erroneous records – individuals that meet the SPD inclusion rules but are in fact not part of the usually resident population that we are estimating.
As found in previous simulations, over-coverage in the SPD causes overestimation of population estimates when coverage adjustment is made using DSE. When we apply the DSE approach outlined previously to our SPD V2.0, we achieve a relative bias (RB) and relative root mean square error (RRMSE) of 7.7% (an over-estimate) and a relative standard error (RSE) of 0.3% at the national level. These three measures of performance are defined in Section 6 and Annex A.
Creating an "active" SPD
We have a matching algorithm that is automated and will include some errors. As discussed in Section 5, false negatives (or missed matches) contribute to most of this error and could inflate our DSE estimates.
Despite this, erroneous records may still cause biases in our estimates when applying DSE. Therefore, we've attempted to refine SPD V2.0 to minimise over-coverage, by removing suspected erroneous records. The majority of links in the SPD are made between the PR and CIS. Individuals aged 20 to 59 years showed the greatest levels of over-coverage within SPD V2.0 when compared with census estimates, being most likely to be non-usually resident. Therefore, only these records are considered as candidates to be removed and modelled in the creation of the "active" SPD. These records account for 22.8 million records, of which 15% didn't link to census or were not usually resident. A more detailed description of the modelling approach used to produce the "active" SPD can be found in Annex B.
Using variables available in administrative data sources, a score is created intending to represent the likelihood of an administrative record being "active" in SPD V2.0.
The mix of binary and categorical variables used as predictors are:
- registered as migrant from overseas with a general practitioner (GP)
- income band from Pay As You Earn (PAYE) data
- household size
- flagged as out of contact with a GP
- Customer Information System (CIS) start date
- how they were matched between Patient Register (PR) and CIS (strength of the match key)
- location agreement or disagreement between different administrative data sources
A threshold for each 10-year age-sex group is calculated using the Youden index. More information on this is available in Annex B. Records with a score below the threshold are then removed from the SPD V2.0 population.
For this test, a total of 7.8 million low-scoring records are removed, producing an SPD with 47.97 million people. At this stage, the scoring method we've developed is not highly accurate at detecting erroneous records. As a consequence, a proportion of the records removed are in fact part of the usually resident population, which limits the conclusions we can draw from our results. This approach would improve if we could collect data that can distinguish between survey non-response and over-coverage in the SPD.
Despite this, it's our expectation that this method will allow us to construct an SPD that contains a higher proportion of "active" usually resident records, compared with not removing records from the SPD at all. As recommended in previous simulations, this would enable us to produce an SPD that minimises for over-coverage and better meets the assumptions of a DSE framework. However, although an SPD of reduced size with fewer erroneous records will reduce some bias, it will increase the variability of the estimates (see Table 1).
When using this "active" SPD, we see a change in the national RB and RRMSE when DSE is applied. Table 1 shows that we now have a 3.7% over-estimate, compared with 7.7% before inactive records were removed. One of the consequences of removing these records is an increase in the variability of the estimates (RSE). However, the overall RRMSE makes this appear to be our most accurate attempt at population estimates using a DSE adjustment at national level. Although it appears that the overall bias has reduced, there may be other sources of bias (such as dependency bias and heterogeneity biases) influencing this change that we currently can't measure. This limits the conclusions we can draw from these results.
Performance at a national level
| SPD Type | RB (%) | RRMSE (%) | RSE (%) |
|---|---|---|---|
| SPD V2.0 | 7.65 | 7.66 | 0.27 |
| "Active" SPD | 3.72 | 3.74 | 0.37 |
Download this table Table 1: Performance of dual-system estimation
.xls .csvFigure 5 shows an analysis of our results for the “active” SPD with DSE by age and sex.
Figure 5: Relative bias and relative root mean square error performance by five-year age and sex, dual-system estimation
England and Wales, 2011
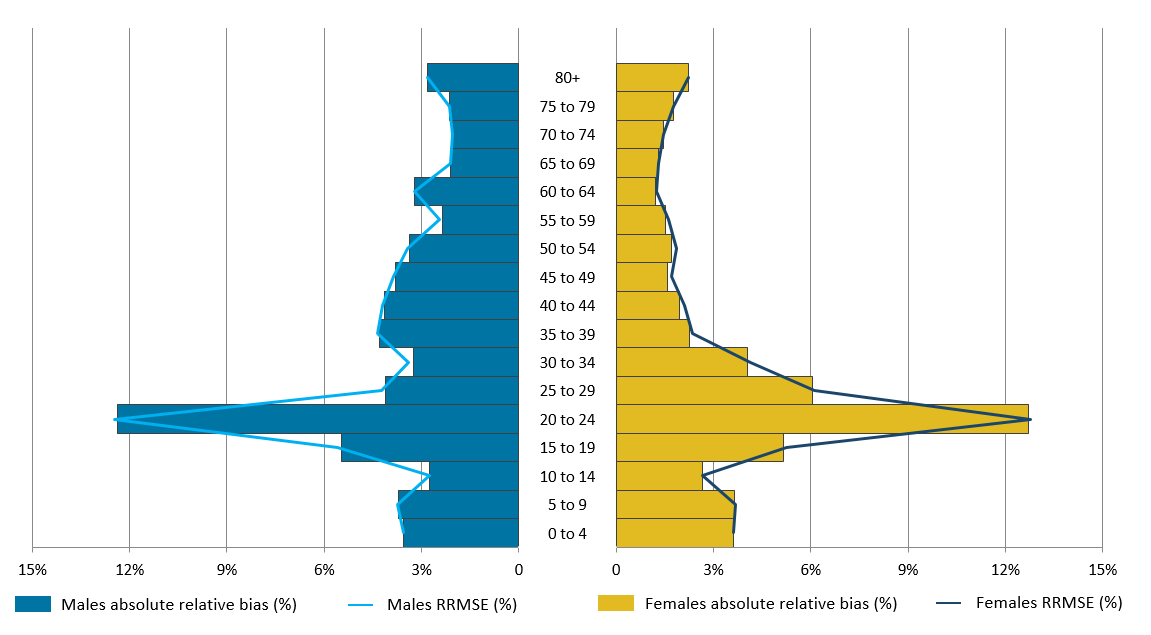
Notes:
RRMSE – Relative root mean square error (a measure of accuracy combining relative bias and relative standard error).
The relative bias is presented in its absolute form to be comparable with the RRMSE value.
Download this image Figure 5: Relative bias and relative root mean square error performance by five-year age and sex, dual-system estimation
.png (45.7 kB) .xls (31.2 kB)Figure 5 shows the absolute RB and the corresponding RRMSE values for each age-sex group. The bias is presented in its absolute form to be comparable with the RRMSE value. In the case of DSE, the RB is always positive and produces an over-estimate for each age-sex group. In each run of estimation at a national level (see Table 1), the RB and RRMSE are very similar and the RSE values are very small for each age-sex group. This suggests that, at a national level, the overall accuracy of the estimates is explained by the bias and there is little variability in the estimates. However, we expect the variability to increase at a local level.
Figure 5 shows that the RB ranges from 1.2% to 12.7%, with the bias for 20- to 24-year-olds being largest for both males and females. As this age group comprises of a population with a higher proportion of students, graduates and young professionals that move addresses more frequently, it's likely that lower proportions of records will match between the survey and the SPD, particularly in the same locations. A low match rate induces a positive bias, which could explain why we see this.
Performance at local authority level
The quality of our estimates varies by local authority. Figure 6 shows the proportion of local authorities at each percentage point difference from the 2011 Census estimates for SPD V2.0 and the "active" SPD with DSE.
Figure 6: Local authority distribution of difference from census estimates, dual-system estimation
England and Wales, 2011
Source: Office for National Statistics
Notes:
SPD - Statistical Population Dataset.
DSE – Dual-system estimation.
Download this chart Figure 6: Local authority distribution of difference from census estimates, dual-system estimation
Image .csv .xlsThe overestimation of the DSE adjustment seen at a national level is reflected at local authority level. However, the magnitude of this is not constant across every local authority. Figure 6 shows that the DSE adjustment tends to cause overestimation when compared with the 2011 Census estimates.
Figure 6 also shows that the SPD V2.0 population estimates generally perform better against the 2011 Census estimates, compared with applying a DSE adjustment to SPD V2.0. By comparing SPD V2.0 estimates with census estimates, we can assess the coverage issues within the administrative data. In the context of an Administrative Data Census, the PCS would be used to assess this. From this assessment, we can see that an adjustment is required to ensure higher quality of our administrative data-based estimates. However, Figure 6 suggests that DSE is not a sufficient adjustment method for this SPD.
| Quality standard | Number of local authorities | Cumulative percentage (%) |
|---|---|---|
| P1: within plus or minus 3.8% | 247 | 70.98 |
| P3: within plus or minus 8.5% | 327 | 93.97 |
| Greater than plus or minus 8.5% | 21 | 100.00 |
Download this table Table 2: The number of local authorities within P1 and P3 quality standards for dual-system estimation
.xls .csvTable 2 shows that after DSE has been applied, the majority (71%) of local authorities fall within plus or minus 3.8% difference from census estimates and 94% within plus or minus 8.5%. Although this suggests that the majority of local authorities fall within the quality targets, this is lower than the 96% of local authorities within plus or minus 3.8% and 99% within plus or minus 8.5% when using SPD V2.0 without a DSE adjustment. This demonstrates that DSE is not a perfect adjustment.
Table 3 displays the 10 local authorities with the highest RB values after the DSE adjustment is applied to the "active" SPD, all showing large overestimation ranging from 12.5% to 39.2%. All 10 of the local authorities are either London boroughs or university towns and cities. This is consistent with findings from applying DSE to SPD V2.0, although the RB and RSE values for these local authorities are generally larger than for the "active" SPD. However, as we can't identify the sources of bias, we can't determine the optimum SPD for use with DSE.
The results shown in Table 3 are expected because young adults, especially students, are a more transient population and are less likely to have up-to-date address information on administrative records. This is consistent with our results seen in Figure 5 for 20- to 24-year-old males and females.
| Rank | Local authority | RB (%) | RRMSE (%) | RSE (%) | Match rate in the same OA (%) |
|---|---|---|---|---|---|
| 1 | City of London | 39.2 | 39.2 | 0.5 | 64.7 |
| 2 | Westminster | 30.3 | 49.9 | 39.8 | 67.8 |
| 3 | Oxford | 20.0 | 23.5 | 12.4 | 66.1 |
| 4 | Tower Hamlets | 18.0 | 20.0 | 8.8 | 70.8 |
| 5 | Kensington and Chelsea | 17.6 | 29.6 | 23.9 | 67.2 |
| 6 | Cambridge | 17.3 | 20.1 | 10.3 | 68.6 |
| 7 | Islington | 15.4 | 17.3 | 7.8 | 70.1 |
| 8 | Bournemouth | 13.1 | 23.6 | 19.7 | 78.9 |
| 9 | Newham | 13.1 | 14.4 | 5.9 | 70.8 |
| 10 | Camden | 12.5 | 14.4 | 7.2 | 69.3 |
Download this table Table 3: Top 10 local authorities with the largest relative bias and match rates
.xls .csvAs expected, for the majority of local authorities listed in Table 3, the RSE is larger at a local level than at a national level. This demonstrates that the lower the geography, the more variability there is in the estimates.
Table 3 also shows the match rate of records in the same output area (OA) on the SPD and PCS, as a percentage of the total SPD records in these local authorities. We see that these match rates for the majority of local authorities with high biases are relatively low. A low match rate along with a high positive bias could suggest that issues remain with erroneous records, SPD records listed in the wrong location, and missed matches between the SPD and PCS. However, we still can't determine the true source of the bias as we can't distinguish between matching error and coverage error.
New linkage approaches at ONS could improve the quality of matching which, in conjunction with the data collection design of a PCS, could provide more direct measures of over-coverage.
Back to table of contents8. Weighting class estimation research
This section describes how we've applied the principles of the alternative estimation method of weighting class estimation (WCE) to our 2011 Statistical Population Dataset (SPD) V2.0 data, to produce coverage-adjusted population estimates.
How have we applied WCE to our SPD?
We've previously published Research Outputs on producing household estimates from "occupied addresses" from administrative data. A similar approach described in that report to define a household, using Unique Property Reference Numbers1 (UPRNs) from the product AddressBase2, has been used in this research. For the purposes of this article, we use the term "households" to describe the use of occupied addresses in the WCE context.
We've developed an automated matching methodology that links address records to AddressBase to assign a UPRN to SPD records. The Patient Register (PR), Customer Information System (CIS) and English School Census (ESC) are all supplied to Office for National Statistics (ONS) with individuals' address records.
To determine the household that an individual is part of, UPRNs were assigned to person-level SPD records based on the ability to link individuals' address records on the PR or CIS to AddressBase. While the majority of records on the SPD can be assigned to a UPRN, approximately 2.2 million (4%) of SPD records weren't successfully matched on addresses and can't be formed into households for this estimator. These remain unadjusted for in our estimates and we expect to underestimate the population because of this.
UPRNs are also assigned to census records by linking the census data to AddressBase, using the same matching algorithm as used for the SPD. UPRNs found in the SPD but not in the Population Coverage Survey (PCS) are categorised as a non-responding household.
The 1% PCS sample, in this research, is drawn in the same way as described for DSE using census data (see Section 7). Sampling weights are calculated and applied to the population counts in the same way as previously described for DSE to reflect the population size in the sampled area.
We can use auxiliary information from the SPD to find out the characteristics of households not responding to the survey. We do this by applying the class weight to those with similar characteristics. This class weight is applied to households in that class in the stratified area, which in this research is at middle layer super output area (MSOA) level, to adjust for non-response for classes of households.
By stratifying at MSOA, we generally meet the assumption that cell sizes are greater than 30. Our research found that stratifying by lower geographies results in lower cell sizes, which can introduce biases to our estimates. We also aggregate individuals aged 80 and over to account for this assumption.
Although the weighting classes approach is based on linking households, individual characteristics of responders are required to form some of the classes we have used in this research. Other biases may be introduced as we could lose homogeneity within these groups by aggregating records. As mentioned in Section 5, a hard-to-count (HtC) index could be used to improve our ability to meet this assumption. However, further research is required to develop an administrative data equivalent.
Four types of classes have been considered so far:
- total – households with no further stratification
- direct – households stratified by age and sex
- type – households stratified by the type of household residence (young adults, for example)
- size – household stratified by the size of the household
As with DSE, a ratio weight is applied at local authority, age and sex level once these adjustments have been made to reduce the variance and provide final estimates for the desired total population of England and Wales. Although WCE is applied at a household level, estimates are aggregated over the 100 simulated PCS samples and produced by local authority and five-year age and sex, as with DSE. This enables comparisons with census and DSE estimates.
For this estimator, we use SPD V2.0, rather than the "active" SPD described in Section 7, when applying the WCE method. This is because WCE is less sensitive to erroneous records on the SPD, compared with DSE – an issue that the "active" SPD attempts to deal with. Furthermore, SPD V2.0 has better coverage of occupied addresses, which is required to achieve high-quality address matching.
Performance at a national level
| Version | RB (%) | RRMSE (%) | RSE (%) |
|---|---|---|---|
| Total | -7.01 | 7.02 | 0.21 |
| Direct | -2.02 | 2.04 | 0.27 |
| Household type | -2.12 | 2.13 | 0.23 |
| Household size | -6.87 | 6.87 | 0.18 |
Download this table Table 4: Performance of weighting class estimation
.xls .csvTable 4 displays the performance measures of applying total, direct, household type and household size WCE to SPD V2.0 2011. The negative relative bias (RB) values for each version of WCE are expected given the propensity for within-household non-response, described in Section 5.
At a national level, as with DSE, the RB and relative root mean square error (RRMSE) values for each version of WCE are very similar and the relative standard error (RSE) values are low. This shows that the overall accuracy of these national estimates is explained by the bias and there is little variability in the estimates.
As outlined in Section 6, previous simulation studies have found that the direct WCE has the lowest bias and is most consistent across age-sex groups. The findings from our analysis support this, as Table 4 shows the RB for the direct version of WCE is considerably smaller (negative 2.0% underestimate, relative to the 2011 Census estimates), compared with the other versions of WCE.
Figure 7: Percentage difference from census estimates for males by five-year age groups, weighting class estimation
England and Wales, 2011
Source: Office for National Statistics
Notes:
- SPD – Statistical Population Dataset.
Download this chart Figure 7: Percentage difference from census estimates for males by five-year age groups, weighting class estimation
Image .csv .xls
Figure 8: Percentage difference from census estimates for females by five-year age groups, weighting class estimation
England and Wales, 2011
Source: Office for National Statistics
Notes:
- SPD – Statistical Population Dataset.
Download this chart Figure 8: Percentage difference from census estimates for females by five-year age groups, weighting class estimation
Image .csv .xlsFigures 7 and 8 show that while there is some variation in the bias across the age-sex groups in the direct WCE results, it is less than the other versions of WCE for most age groups. This suggests that direct WCE is our most promising method for producing population estimates using a WCE adjustment at a national level. This is consistent with the findings from previous simulation studies.
Focusing on the direct WCE results, it should be noted that for females aged 20 to 24 years, the bias is positive and we overestimate this population group, compared with the census estimates. This could be because of heterogeneity within classes, whereas it is assumed that non-response is homogenous (the same) within classes. Another explanation is that this is caused by the fact that over-coverage is higher in survey non-responding households, whereby non-usual residents (such as short-term migrants) interact with government services (and appear in the SPD) but don't respond to the survey because of their residence status. However, we can't be certain as we don't have sufficient data to explore this.
Figure 9 shows the absolute RB and the corresponding RRMSE values for each age-sex group. The bias is presented in its absolute form to be comparable with the RRMSE value. In the case of WCE, some relative bias values are negative and some are positive. Figures 7 and 8 give an indication of the direction of the bias for each age-sex group.
Figure 9: Relative bias and relative root mean square error performance by five-year age and sex, weighting class estimation
England and Wales, 2011
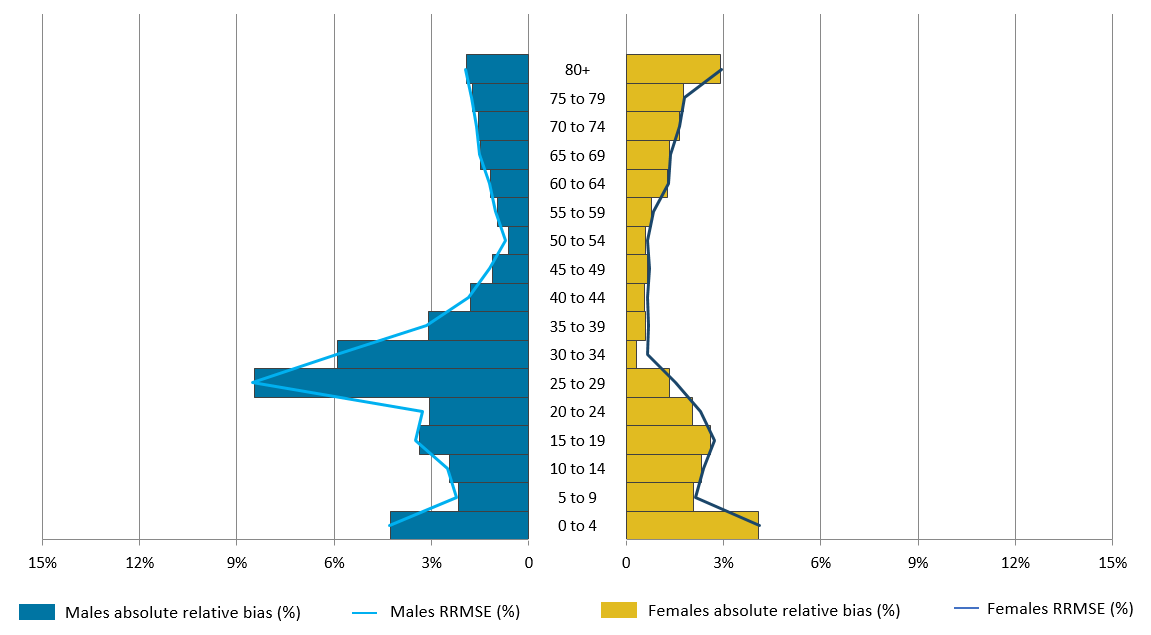
Source: Office for National Statistics
Notes:
- RRMSE – Relative root mean square error (a measure of accuracy combining relative bias and relative standard error).
- The relative bias is presented in its absolute form in order to be comparable with the RRMSE value.
Download this image Figure 9: Relative bias and relative root mean square error performance by five-year age and sex, weighting class estimation
.png (43.9 kB) .xls (23.0 kB)Figure 9 shows that for the majority of age-sex classes, when direct WCE is applied to SPD V2.0 the RB and RRMSE values are very similar. As seen in Table 4, at a national level, this shows that the accuracy of the estimates at age-sex breakdowns is largely explained by the bias and there is minimal variation in the estimates. As with DSE this suggests that, at a national level, the overall accuracy of the estimates is explained by the bias and there is little variability in the estimates. However, we expect the variability to increase at a local level.
Performance at local authority level
The quality of our estimates varies by local authority. Figure 10 shows the proportion of local authorities at each percentage point difference from the 2011 Census estimates for SPD V2.0 and SPD V2.0 with direct WCE.
Figure 10: Local authority distribution of difference from census estimates, weighting class estimation
England and Wales, 2011
Source: Office for National Statistics
Notes:
- SPD – Statistical Population Dataset.
- WCE – Weighting class estimation.
Download this chart Figure 10: Local authority distribution of difference from census estimates, weighting class estimation
Image .csv .xlsThe effects of the direct WCE adjustment at local authority level mirror what we see at a national level. Figure 10 shows that the weighting class adjustment causes a larger proportion of local authorities to underestimate (relative to census), compared with our published SPD V2.0 population estimates.
Table 5 shows that after the WCE adjustment is applied to SPD V2.0, 89% of local authorities fall within plus or minus 3.8% difference from census estimates and 98% within plus or minus 8.5% difference. This leaves 2% of local authorities that fall outside of the P3 quality target. This appears to be an improvement when compared with DSE and is closer to the results from SPD V2.0 without a coverage adjustment. However, we can't draw generalisable conclusions from our results because we can't measure all components of bias.
| Quality standard | Number of local authorities | Cumulative percentage (%) |
|---|---|---|
| P1: within plus or minus 3.8% | 311 | 89.37 |
| P3: within plus or minus 8.5% | 342 | 98.28 |
| Greater than plus or minus 8.5% | 6 | 100.00 |
Download this table Table 5: The number of local authorities within P1 and P3 quality standards for weighting class estimation
.xls .csv
| Rank | Local authority | RB (%) | RRMSE (%) | RSE (%) | UPRN match rate (%) |
|---|---|---|---|---|---|
| 1 | City of London | -18.3 | 18.3 | 0.0 | 52.9 |
| 2 | Westminster | 12.8 | 32.0 | 29.4 | 82.4 |
| 3 | Gwynedd | -12.2 | 13.9 | 6.7 | 81.2 |
| 4 | Manchester | -9.0 | 10.1 | 4.4 | 88.9 |
| 5 | Richmondshire | -9.0 | 10.4 | 5.1 | 92.1 |
| 6 | Forest Heath | 8.5 | 38.5 | 37.7 | 97.9 |
| 7 | Kensington and Chelsea | 7.5 | 25.0 | 23.9 | 84.4 |
| 8 | Nottingham UA | -7.1 | 8.6 | 4.9 | 90.1 |
| 9 | Enfield | -7.0 | 8.3 | 4.6 | 93.7 |
| 10 | Hammersmith and Fulham | 6.7 | 15.5 | 14.0 | 90.0 |
Download this table Table 6: Top 10 local authorities with the largest relative bias and Unique Property Reference Number match rates
.xls .csvTable 6 displays the local authorities with the largest biases after the WCE adjustment is applied. Six of these show a large underestimation (with RB values ranging from negative 7.0% to negative 18.3%). However, the local authorities with the highest positive biases, including Westminster and Kensington and Chelsea, show a large overestimation.
Richmondshire has a large military population, which doesn't appear in the administrative data (although these military personnel are added as aggregate estimates to the published SPD V2.0 population estimates). This results in under-coverage of this local authority in the SPD, which could explain why we see a negative bias.
Forest Heath also contains a large military population. However, we see a positive bias of 9%. This is unexpected and suggests that there are other biases influencing the overall relative bias. Further work is required to be able to measure and account for these additional biases.
As expected, for the majority of local authorities listed in Table 6, the RSE is larger at a local level than at a national level. This demonstrates that the lower the geography, the more variability there is in the estimates.
Table 6 also shows the proportion of records that we could link a UPRN to for these local authorities, as a percentage of the total number of SPD records. We see that the match rate for City of London is very low – only approximately half of SPD records could be linked to a UPRN. Within-household non-response on the PCS is thought to be driving the overall negative bias seen with a WCE approach.
Additionally, the quality of the address information present on the administrative data, as well as the difficulty in assigning UPRNs to complex addresses, could be a contributing factor to the high biases seen here.
Notes for: Weighting class estimation research
A Unique Property Reference Number (UPRN) is a unique alphanumeric identifier for every spatial address in Great Britain and can be found in Ordnance Survey's address products.
AddressBase – an Ordnance Survey address product compiled from local authority, Ordnance Survey and Royal Mail address lists.
9. Comparing DSE with WCE
As we can't identify the components of bias, we can't draw conclusions from the results about which Statistical Population Dataset (SPD V2.0 or the "active" SPD) is optimal for dual-system estimation (DSE). Based on measures of relative bias, we can see that DSE appears to perform better with our first attempt at producing an active SPD (see Table 1). However, our ability to identify more active records is limited without more activity data available.
These same problems apply to weighting class estimation (WCE). Our analysis also shows that adjusting for non-response by grouping survey non-responders into classes stratified by age and sex (WCE direct) appears to produce the least biased results out of the other classes tried in this research. The approaches for DSE and WCE with the least bias at a national level are compared in this section.
| Version | RB (%) | RRMSE (%) | RSE (%) |
|---|---|---|---|
| “active” SPD with DSE | 3.72 | 3.74 | 0.37 |
| SPD V2.0 with direct WCE | -2.02 | 2.04 | 0.27 |
Download this table Table 7: Performance of dual-system estimation and weighting class estimation
.xls .csvTable 7 summarises the performance measures of both approaches. At a national level, we see that for all three measures, the direct WCE approach applied to SPD V2.0 appears to perform better than the DSE approach to the "active" SPD.
This is also demonstrated when we compare the two methods by age and sex. Figures 11 and 12 show the percentage difference from the 2011 Census estimates for each of these methods and for the published SPD V2.0 estimates.
Figure 11: Percentage difference from census estimates for males by five-year age group
England and Wales, 2011
Source: Office for National Statistics
Notes:
- SPD - Statistical Population Dataset.
- DSE - Dual-system estimation.
- WCE – Weighting class estimation.
Download this chart Figure 11: Percentage difference from census estimates for males by five-year age group
Image .csv .xls
Figure 12: Percentage difference from census estimates for females by five-year age group
England and Wales, 2011
Source: Office for National Statistics
Notes:
- SPD - Statistical Population Dataset.
- DSE - Dual-system estimation.
- WCE – Weighting class estimation.
Download this chart Figure 12: Percentage difference from census estimates for females by five-year age group
Image .csv .xlsFigures 11 and 12 show that for some age-sex groups in both approaches, the percentage difference from the census estimates is smaller compared with the published SPD V2.0 estimates. Our DSE results are slightly closer than our published SPD V2.0 to the census estimates only for males aged 40 to 49 years.
However, the most notable improvements are seen in the WCE approach for males aged 35 to 59 years and for females aged 25 to 64 years. This suggests that applying an estimation method such as WCE could improve our current administrative data-based population estimates for some age-sex groups. This could be a true reflection of applying these coverage adjustments. However, further research is required to understand the components of this overall bias.
Figure 13: Local authority distribution of difference from census estimates
England and Wales, 2011
Source: Office for National Statistics
Notes:
- SPD - Statistical Population Dataset.
- DSE - Dual-system estimation.
- WCE – Weighting class estimation.
Download this chart Figure 13: Local authority distribution of difference from census estimates
Image .csv .xlsFigure 13 demonstrates that the majority of local authorities show a pattern of underestimation compared with the census estimates for WCE but show an overestimation when DSE is applied. This suggests that the adjustment made in DSE for non-response introduces a positive bias, which could be driven by erroneous SPD records and matching error.
Compared with WCE, the adjustment made for non-response is showing a larger negative bias, which could be due to within-household non-response on the PCS. This demonstrates limitations of both methods when their theoretical assumptions can't be met.
Back to table of contents10. Summary and future developments
We've demonstrated our research into producing coverage-adjusted population estimates using administrative data by applying two different estimation approaches to our Statistical Population Datasets (SPDs) – dual-system estimation (DSE) and weighting class estimation (WCE). This is in line with our framework for producing population estimates using linked record-level administrative data alongside an Administrative Data Census.
Our results show that there is a higher prevalence of bias in the results compared with variance. For most age-sex groups, DSE produces a positive bias and WCE produces a negative bias. We've demonstrated a reduced level of overall relative bias when comparing different versions of these methods, which may be a true reflection of the adjustments. However, we can't measure or account for the components of bias (such as dependency and heterogeneity) that could be driving this reduction. Therefore, we can't currently draw generalisable conclusions from our results about which of these adjustment methods would perform best in an Administrative Data Census.
We've demonstrated our first attempt to deal with over-coverage by developing a model to remove erroneous records to create our "active" SPD. However, our approach to removing these records was only modelled for 20- to 59-year-olds with an NHS Patient Register (PR) or Department for Work and Pensions' (DWP) Customer Information System (CIS) record linked in the SPD. More sources of administrative data, including "activity" data, are required to improve the quality of these estimates. This will enable us to have more evidence to decide if and where an individual is usually resident. "Activity" can be defined as an individual interacting with an administrative system, for example:
- for National Insurance or tax purposes
- when claiming a benefit
- attending hospital
- updating information on government systems in some other way
Only demographic information (such as name, date of birth and address) and dates of interaction are needed from such data sources to improve the coverage of our population estimates. Access to more data will help us to develop the construction of our SPDs. In addition to more data, developments to our matching methodology could reduce this further.
In the absence of high-quality "activity" data, we're currently unable to distinguish between persons on the administrative records that have left the address (over-coverage) and those who haven't responded to coverage surveys (within-household non-response). This is problematic for both DSE and WCE estimation. A future Population Coverage Survey (PCS) that includes an approach for handling over-coverage, such as dependent sampling described in Section 4, would be of benefit to both of these estimators.
For a DSE approach, it would enable the direct measure of over-coverage, which could be incorporated into the adjustment framework. For the WCE approach, it would serve as a prompt for survey respondents to recall other residents that have been missed in the survey enumeration, thereby reducing within-household non-response.
As mentioned in Section 4, we're reviewing international approaches to over-coverage adjustments and considering the legal, ethical and public acceptability basis for including these as part of a future PCS in England and Wales.
Based on the data available in this study, our results suggest that our most promising coverage adjustment method is direct WCE – grouping non-responders by age and sex – when applied to SPD V2.0. This approach results in the smallest relative bias (RB) and relative root mean square error (RRMSE). When compared with other WCE approaches and our best attempt at DSE, direct WCE outperforms on these measures, although the relative standard error (RSE) is still small and similar to the other approaches.
This is contrary to the findings of previous simulation studies (Castaldo et al, 2014), which concluded that direct WCE would only outperform DSE (with an over-coverage and ratio adjustment) where there was no within-household non-response. However, these simulations were based on the assumptions of no erroneous records and perfect matching. Our results demonstrate the effects of applying these coverage adjustments to real SPD data. We acknowledge that we can't control for components of bias as is possible with simulation studies. Further research is required to understand how we might measure these additional biases when using administrative data in the future.
Although the results for direct WCE appear to be more promising, positive biases for some age-sex groups suggest that there could be a violation of the assumption that households within classes are homogenous. This suggests that further development is required to construct classes in a WCE approach to ensure that the violation of this assumption is minimised. However, this is just one explanation. We can't be sure that this is the only cause until we can measure and account for other sources of bias.
The two methods described in this article require a PCS to adjust estimates of the population of England and Wales. We undertook a small-scale PCS test on a sample of 4,000 households in September 2017 and will be undertaking a further test in 2018 with the aim of producing population estimates for England Wales for five-year age-sex groups. We'll provide an update on the PCS test we carried out in 2017 later this year, where our research is focusing on response rates to a voluntary survey.
As a full-scale PCS isn't currently in place, we've only been able to produce these estimates for 2011, using a sample of 2011 Census data as a proxy for the PCS. We're currently exploring the potential use of Labour Force Survey (LFS) data as the basis for producing similar studies for more recent years. However, these estimates would likely be limited to national and regional level estimates.
Back to table of contents11. Annex A: Equations for performance measures
Where j is the simulation number and n the total number of simulations:
12. Annex B: “Active” Statistical Population Dataset methodology
Summary
The Statistical Population Dataset (SPD) V1.0 annual research update in October 2015 set out the production of an SPD, the combination of data sources used and included population estimates from SPD V1.0. Our November 2016 research update developed this approach further and focused on increasing the coverage of age-sex groups that were under-represented in SPD V1.0 through the production of SPD V2.0.
The methods developed to support SPD construction were largely based on identifying individuals that have multiple registrations with different government datasets. Our research indicates that appearing on multiple data sources is indicative that a person is likely to be usually resident in England and Wales. However, we have always acknowledged that delays in de-registering people from these datasets when leaving the country is likely to result in a certain (and currently unmeasurable) amount of over-coverage. Currently there is no legal requirement to notify general practitioners (GPs) or the Department for Work and Pensions (DWP) when leaving the country. Therefore, we expect that over-coverage is prevalent on our SPDs.
In our methodological update in 2016 we proposed that the focus of our SPD development should concentrate on the use of newly acquired "activity" data in an attempt to identify and remove individuals that are no longer usually resident from the SPD. This is the basis of the "active SPD" that we describe in this article. We now describe the data and methods we've used for determining which records to remove to create the "active SPD".
The definition of usual residence is based on an individual that either had been, or planned to be, permanently resident in the country for 12 months. We've tested a logistic regression model to predict the probability that an individual may be usually resident, based on a range of characteristics.
Selecting predictor variables
The first step to producing the model was identifying those variables that may be predictive of usual residence. These variables were chosen through exploratory data analysis. For this, we investigated associations between residency status and other individual variables, which we believed to be influential.
Alongside this, we also plotted variables graphically to help us recognise patterns in the data. Combinations of variables were then included within the models to test whether their inclusion was statistically significant in predicting usual residency. A full range of variable combinations were trialled and this led to the final selection of variables, which are described in this section.
Previously living overseas
When an individual immigrates into the country and registers with a GP, they are given a Flag 4 indicator within the NHS Patient Register (PR). This indicates that the individual was previously living overseas. We found that the Flag 4 migration indicator is a strong indicator that a person may no longer be resident, as in many instances they will have been resident on a temporary basis.
Output area difference
Where an individual has a different geographic location between the PR and Customer Information System (CIS), they received a flag. This disagreement between the data sources was found to indicate that an individual may be mobile and therefore less likely to be usually resident.
Income band
Those with a low or zero income registered through the Pay As You Earn (PAYE) taxation system were found less likely to be usually resident than those with a higher income.
Occupancy
Addresses with only a single occupant, or addresses with six or more occupants were found less likely to be usually resident. The number of individuals at an address on the PR was found to be influential in predicting usual residence.
Out of contact with doctor (FP69)
An FP69 flag can be placed on a PR record if an enquiry letter is sent by a Primary Care Authority after the individual has been out of contact with the GP practice for more than six months. Following this, the patient can be removed from the GP practice list after six months unless contact is made with the individual. This flag may indicate that this individual is no longer at the address and therefore possibly not resident in the country.
Years registered at an address on the CIS
The number of years an individual has been registered as living at an address on the CIS system. The variable was derived by calculating the time difference between the 2011 Census date and the registration of address start date on the CIS. Those individuals that indicated that they hadn't lived at the address for long were less likely to be usually resident than those who had been living at the address for a number of years.
Match key number
Match keys are used to link individuals between administrative datasets (as described in more detail in Beyond 2011: Matching anonymous data (PDF, 320KB). These have a hierarchy of strength. It was expected that the stronger the match key used, the more likely the individual is to be usually resident. This is because records linked on weaker match key may relate to people whose administrative record is out of date or have been incorrectly linked.
Sampling
To model the probability of usual residence using a logistic regression, we need a sample dataset where the usual resident status is known for individuals included in that sample. This dataset serves as a "training dataset", where the predictor variables described previously are used to model the known outcome of usual resident status of these records in the sample. The sample should be representative but independent from the full population that the model is finally applied to.
For the 2011 SPD, data are available from the census, which provides some information about usual residence. For non-census years, which we may consider applying similar models to in future, it is intended that these data would come from a Population Coverage Survey (PCS). It should be noted that there are considerable limitations with using census data and data from an independent PCS data for the model described here.
Critically, we're unable to distinguish between persons that don't appear in censuses and surveys because they are no longer usually resident, or because they haven't responded to the survey. For this reason, we're exploring alternative approaches to handling over-coverage other than the modelling approach described here, such as dependent sampling (see Sections 4 and 10).
To select a sample for the model used in this study we linked records from the PR, CIS and 2011 Census. These data were then sampled to represent the data that may be provided by a PCS. A 1% sample (244,655 records) of the full dataset was drawn, stratified by age, sex, region and residency status. The sample was stratified by age, sex and region to give good coverage across the population. Within the full sample, however, some age and sex groups have as low as 6% of individuals classed as not usually resident. This resulted in only a small number of individuals in the non-usual resident category that is of most interest to the study. This small number would have limited the ability of the model to identify the characteristics of non-usual residents and therefore ability to correctly classify these individuals.
To allow the model to better identify non-resident individuals, residency status was included as an additional stratifying variable in the sampling process. This gave an approximately evenly split coverage of those usually resident (50%) and not usually resident (50%) within the base sample.
The model was only applied to individuals aged between 20 and 59 years. These were the ages that showed the greatest levels of over-coverage likely to be prevalent on SPD V2.0. Those outside this age range were found to be less likely to interact with key sources and therefore, the data available were less detailed. Further activity data would be required to model the probability of usual residence within these age groups.
The number of individuals modelled by age and sex groups can be seen in Table 8.
| Age | Male | Female |
|---|---|---|
| 20 to 29 | 36,441 | 29,244 |
| 30 to 39 | 39,086 | 27,463 |
| 40 to 49 | 38,133 | 26,798 |
| 50 to 59 | 26,451 | 21,039 |
Download this table Table 8: Number of individuals used to train the logistic regression model by age and sex
.xls .csvLogistic regression model
Logistic regression provides coefficients that measure each independent variable's (such as being out of contact with a doctor) partial contribution to variations in the outcome (resident or non-resident status). These coefficients can be used to predict usual residence for all other records on the SPD that are not included in the sample.
Our final model was split by sex and 10-year age groups, allowing the influence of the covariates to vary, dependent on the age and sex of the individual. The model was then applied to the subset of 22.8 million PR or CIS records from SPD V2.0 of those aged between 20 and 59 years. The predicted probability of residence was made for each of the records belonging to this group.
Thresholds
To use a logistic regression model for classifying whether someone is usually resident or not, an optimum threshold must be identified in the probability distribution. Those records with probabilities above this threshold are classed as "usually resident" and those below classed as "not usually resident". Various points of the distribution were analysed to determine the probability score that would give optimum results for our DSE study.
Generally, the selection of the thresholds depends on the use of the model and the priorities of the modeller. A very high threshold may be chosen if the risk of false positive results (incorrectly including individuals on the SPD when they are no longer resident) is of most concern. Similarly, if the risk of false negative results (incorrectly excluding individuals from the SPD) is of most concern then a very low threshold can be set.
For the purposes of DSE, which is applied after the modelling process to produce final population estimates, false positives are of major concern as they will remain unadjusted as a source of over-coverage in the estimates. However, setting the threshold excessively high to avoid this would greatly increase the variability and stability of the DSE.
For the model applied to SPD V2.0, a higher threshold produced only a small decrease in false positives. Meanwhile, the selection of a higher threshold notably decreased the number of those correctly predicted as usually resident. This effect can be seen in Figure 14, using females aged 40 to 49 years as an example.
Figure 14: Females aged 40 to 49 years logistic regression classification plot
England and Wales, 2011
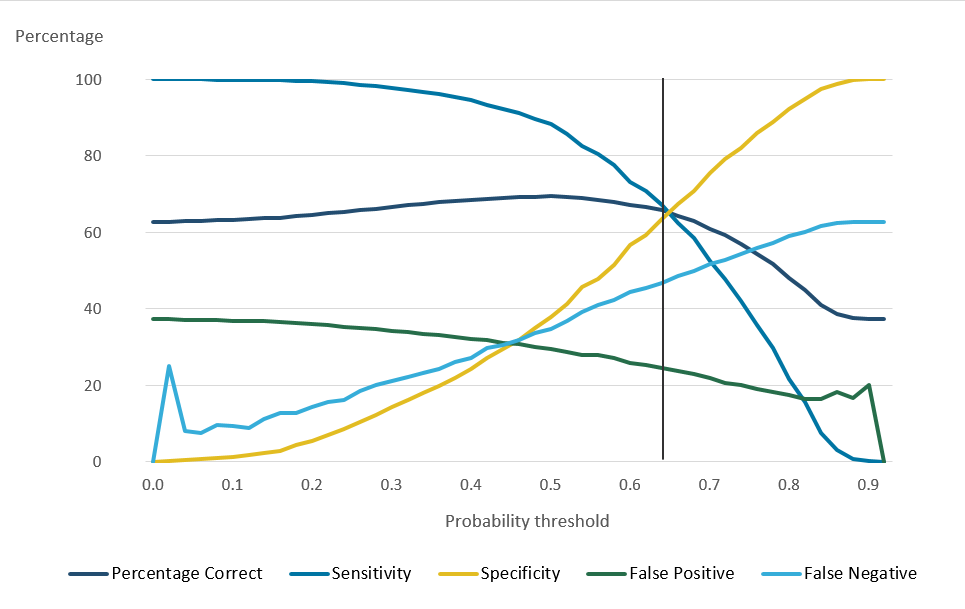
Source: Office for National Statistics
Download this image Figure 14: Females aged 40 to 49 years logistic regression classification plot
.png (43.0 kB) .xls (24.6 kB)Due to the minimal improvement available in false positive rate and significant detriment to overall model performance, the threshold selected was the maximisation of overall correct predictions. This location is also called the Youden index and describes the maximum combination of sensitivity (correct positive prediction) and the specificity (correct negative prediction). These can be calculated using the following equations:
The Youden index is one of the most common threshold selection criteria. The formula for this is as follows:
The thresholds selected for each 10-year age-sex group for our model are detailed in Table 9.
| Sex | Age | Concordance (c) | Threshold |
|---|---|---|---|
| M | 20 to 29 | 0.714 | 0.30 |
| M | 30 to 39 | 0.752 | 0.36 |
| M | 40 to 49 | 0.765 | 0.44 |
| M | 50 to 59 | 0.766 | 0.54 |
| F | 20 to 29 | 0.707 | 0.38 |
| F | 30 to 39 | 0.724 | 0.52 |
| F | 40 to 49 | 0.712 | 0.64 |
| F | 50 to 59 | 0.699 | 0.68 |
Download this table Table 9: Model concordance and selected threshold
.xls .csvDiagnostics
To ensure that the model was operating correctly, the model was checked to ensure that all the assumptions of a logistic regression model were being accounted for. To begin, we checked that no important variables were omitted or incorrectly included. To do this, we conducted a test, in which the model is rerun using the model predicted probabilities and predicted probability squared as predictors.
If the predicted probability is statistically significant and predicted probability squared isn't statistically significant, this suggests that we have chosen meaningful predictors. If, however, the predicted probability squared is also significant, this suggests that we may have some model misspecification, such as not including all meaningful variables or omitting necessary interaction effects.
We also obtained the concordance (c) statistic, which is calculated as the area under the receiver operating characteristic (ROC) curve – a graphical method of assessing model fit. Possible values of the concordance (c) statistic range between 0.5 and 1.0 and represent the relationship between the true positive rate (sensitivity) and the false positive rate (1 – specificity). Generally, values closer to 1 suggest better model fit. The results of this can be seen for each model in Table 9, with values ranging from 0.699 to 0.766, which suggests an acceptable model fit.
Table 10 shows the performance of the classification model. As can be seen from the table, the model produces a comparatively low number of false positives (incorrectly classified as usually resident). However, a false positive result of just under 6% still indicates that over-coverage will remain on the active SPD after using this model approach.
The model does suffer from a high number of false negatives (incorrectly classified as not usually resident). While DSE is more likely to account for these, we will have seen an increase in the variance of DSE results as a consequence of this. Overall, the model predicted the majority of the usual residents correctly, but was less successful at classifying non-usual residents.
| Count | Percent (%) | |
|---|---|---|
| True Positive | 13,610,000 | 59.67 |
| False Positive | 1,251,413 | 5.49 |
| True Negative | 2,188,391 | 9.60 |
| False Negative | 5,757,617 | 25.25 |
Download this table Table 10: Model confusion matrix
.xls .csvSummary
In conclusion, the modelling approach used to create the "active" SPD provided a number of insights into the characteristics of those who aren't usually resident within our administrative data. However, for this model to be viable we would need more detailed activity data that are very good at predicting usual residence, and additional information that can distinguish between survey non-response and individuals that have left the country.
We may consider developing this approach, depending on the alternative options we have for designing our PCS (see Sections 4 and 10) and the availability of additional data sources for predicting usual resident status.
Back to table of contentsYou might also be interested in:
- How we are improving population and migration statistics
- How we are improving population and migration statistics
- Methodology for creating uncertainty intervals for mid-year population estimates by single year of age and sex: July 2020
- Admin-based population estimates and statistical uncertainty: July 2020
- Developing our approach for producing admin-based population estimates, subnational analysis for England and Wales: 2011
- Indicative uncertainty intervals for the admin-based population estimates: July 2020
