Indicative uncertainty intervals for the admin-based population estimates: July 2020

We have been working in collaboration with Professor Peter Smith of the University of Southampton to develop measures of statistical uncertainty for Office for National Statistics (ONS) population estimates. "Uncertainty" refers to the quantification of doubt about the estimates. Uncertainty measures for the mid-year local authority population estimates were published in 2017. The methods are described in Methodology for measuring uncertainty in ONS local authority mid-year population estimates: 2012 to 2016.

The methodology uses a range of statistical bootstrapping techniques to create plausible simulated distributions for the population estimates. Bootstrapping is a method for assigning measures of accuracy to sample estimates (Efron and Tibshirani, 1993). Uncertainty intervals are taken from the simulated estimates.

We have built upon and further developed these methods to derive indicative uncertainty intervals for the experimental admin-based population estimates (ABPEs V3.0). We use a benchmark approach, comparing the ABPEs against the 2011 Census. Ultimately, the intention is that statistical uncertainty for the ABPEs will be derived through a Population Coverage Survey.

The ABPEs consist of estimates of the population size produced through linkage of administrative data, including Pay As You Earn (PAYE) and tax credits data, national benefits and Housing Benefit data, English and Welsh school census, Higher Education Statistics Agency (HESA), and data from the Patient Register (PR) and the Personal Demographics Service (PDS).

Methods for the production of the ABPEs are described in the Principles of ABPE V3.0 methodology.

We use the following model:

where:

P_i,j,k is the true, unknown population size for local authority (LA), i=1, ... , 348, sex, j=1,2, and age, k=0, ... , 90

ABPE_i,j,k is the ABPE estimate

LSF_i,j,k is a log-scaling factor (LSF) – a measure of bias in the ABPE estimate

is the error.

By taking the exponential of both sides of this equation, the model can be written as:

We make the simplifying assumption that the error associated with the census is an order of magnitude smaller than the error associated with the ABPE, and therefore set it to zero. Thus:

To estimate the log-scaling factor LSF_i,j,k, we compare the 2011 ABPE estimate, abpe_i,j,k, with the 2011 Census, denoted census_i,j,k, as an external benchmark representing the “true” population size.

Thus, we obtain the observed LSF:

When interpreting the LSFs, a value greater than zero indicates that fewer people have been captured by the ABPE than in the census data (ABPE undercount). Conversely, a value less than zero indicates that more people have been captured by the ABPE data than in the census data (ABPE overcount).

To create plausible simulated values for the LSFs, we need to estimate the error distribution, F. We make the assumption that the variability between LAs within a group of similar LAs is a good proxy for within-LA variability for the LAs within that cluster. We identify groups of similar local authorities through a cluster analysis of the LSF profiles by age and sex. The cluster analysis is run separately for males and females.

For each group of local authorities, a Generalised Additive Model (GAM) is fitted to the LSFs, generating predicted and residual values. The residuals are resampled to simulate an error distribution for each LA, by age and sex. This distribution of errors is added to the observed LSFs, and then back-transformed to generate a distribution of plausible population estimates. A step-by-step summary of the entire methodology is provided in Annex A.

Bear in mind the following caveats when considering these indicative uncertainty intervals:

• These are interim measures of uncertainty, in place until the ABPE methodology is finalised.

• This method does not allow for uncertainty in the 2011 Census estimates.

• Nor does it allow for bias in the ABPEs to change as the intercensal decade progresses; instead, it assumes that bias observed with reference to the 2011 Census is propagated through the decade (further refinement may be possible once the ABPE methodology is finalised).

• There is some circularity in this interim approach, since ABPEs have been tuned to 2011 Census estimates.

For each sex, local authorities (LAs) are clustered based on similar patterns of log-scaling factors (LSFs) by age. K-means cluster analysis is used for consistency with methods used to measure uncertainty in the mid-year population estimates (MYEs). The elbow method, silhouette method, and an ensemble approach were all used to determine the optimal number of clusters. There are five LAs for each sex whose patterns did not, in any way, resemble those of any other cluster because they have large positive and negative LSF values. We begin by describing how the outlier LAs were identified.

Determine outlier local authorities

We calculate the median LSF for each age, separately for males and females. The LSF profiles for all LAs are visually compared against the median. A summary measure of the difference between each LA and the median LSF profile is calculated.

Summary measure to identify outlier LAs

The Manhattan Norm measures how different each LA LSF profile is from the median profile. It is the sum of absolute deviations around the mean, calculated as:

where x_i is the LSF for age i, and x̃_i is the median LSF over all LAs for age i.

Figures 1a and 1b show the distribution of Manhattan Norms for females and males, respectively. LAs with the 10 largest values are given in Table 1. For both sexes, the top five outlie the bulk of the distribution. Outlying LAs are highlighted and labelled in Figures 2a and 2b for females and males, respectively. The median LSF profile for the remaining “normal” LAs is also shown. The profiles of the outlier LAs fluctuate wildly from the median profile.

K-Means clustering

Outlier LAs are excluded from the K-means clustering. We use all ages (0 to 90 years and over) to cluster the LSF profiles.

K-Means clustering diagnostics and choice of number of clusters

Three methods are used to consider the appropriate number of clusters to use: the elbow method, the silhouette method and an ensemble approach. These suggest that the optimal number of clusters is two each for males and females. However, sensitivity analysis shows that the uncertainty intervals are sensitive to the number of clusters used. An important objective in this research is to compare ABPE V3.0 against the previous version, ABPE V2.0. For consistency and comparability, we use four clusters for females and five for males. LAs in each cluster are listed in Annex B.

Median LSF profiles

The median LSF profiles for each cluster are plotted in Figures 3a and 3b for females and males, respectively. LSF values greater than zero indicate ABPE undercount, and less than zero indicate overcount. The plots show an undercount for people of working age, more so for males.

Outlier LAs

Figures 4a and 4b show the LSF profiles for the outlier LAs, together with the median LSF profiles for the "normal" clusters, for females and males, respectively. The outliers have large positive and negative LSF values, differentiating them from the normal clusters. The outlier LAs are therefore allocated their own cluster (one for each sex).

Generalised Additive Models (GAMs) are fitted to the log-scaling factors (LSFs) by cluster. This semi-parametric approach was chosen because Rogers-Castro models that were used in mid-year estimate (MYE) uncertainty research were found to be a poor fit for LSF distributions, particularly for females. The GAMs generate fitted values denoted

and corresponding residuals, denoted r_i,j,k. The clusters are denoted c=1, ... , 11, where clusters 1 to 5 correspond to females (four normal clusters and one for the outlier local authorities (LAs)) and 6 to 11 correspond to males (five normal, one outlier). An example of the data set following all the above processes is shown in Table 2.

For fitting the GAM, 22 knots are used for the age range of 0 to 90 years and over (one extra knot for ages 86 to 90 years, and an additional knot for age 90 years and over to account for the sharp difference in LSFs between ages 89 to 90 years and over). The knots are placed strategically to allow for more flexibility in the curve at minima and maxima. The knot locations were determined by:

• Starting with equally spaced knots (current best)
• Always keeping knots at age 0 to 90 years
• Randomly selecting 20 ages between 1 year and 89 years
• Fitting GAM
• Calculating a goodness of fit statistic (AIC)
• If the new AIC is better than the current best, then making this knot selection the current best
• Repeating 10,000 times (or as much as possible, given time constraints)

We begin by defining a group as a unique combination of cluster, sex and age. For four normal clusters for females and five for males, plus one outlier cluster for each sex, there is a total of 11 clusters. Since there are 91 ages, there is a total of n = 11 x 91 = 1001 groups, each containing between 5 and 121 residuals (the number of local authorities (LAs) in the corresponding cluster).

We standardise the residuals so that the variance for each group is one, sample 1,000 residuals (with replacement) then reverse the standardisation. To standardise the residuals, denoted s_i,j,k, we divide each residual, r_i,j,k, by its within-group standard deviation, σ_c,j,k, that is,

We calculate standardised residuals for each group in the “normal” clusters (1 to 4 and 6 to 10), creating 819 groups each with a variance of one. We assume that each group of standardised residuals follows the same underlying distribution¹, and put them together in one pot (“Pot 1”).

The outlier clusters (5 and 11) are treated differently because of their unusual log-scaling factor (LSF) profiles. Instead of standardising their residuals, we assume the standard deviation is constant across all groups (within a cluster). Each group contains only five residuals, which is insufficient to obtain an accurate estimate of the standard deviation. Therefore, we allocate the raw residuals from cluster 5 to “Pot 2”, and from cluster 11 to “Pot 3”. The distributions of the residuals in each pot are shown in Figures 5a, 5b and 5c for LAs in the “normal” clusters, in the female outlier cluster and in the male outlier cluster, respectively.

For each group in the normal clusters (1 to 4 and 6 to 10) 1,000 standardised residuals are resampled (with replacement) from Pot 1. The selected residuals are un-standardised by multiplying the selected residuals by the group standard deviation, σ_c,j,k.

For each group in clusters 5 and 11, 1,000 residuals are sampled (with replacement) from Pot 2 and 3, respectively. Since these residuals were not standardised, they do not need to be un-standardised.

Each set of 1,000 residuals is a simulated error distribution for all the LAs in the group, that is, it is an estimate of

in the first equation in Section 2. They are then added to the observed LSFs², lsf_i,j,k, to generate 1,000 simulated LSFs for each LA.

From the second equation in Section 2, the 1,000 simulated LSFs are back-transformed by exponentiating them to obtain 1,000 plausible scaling factors, and then multiplied by the published ABPE for LA i. Doing so, we obtain a simulated distribution of population estimates for each combination of sex, j, and age, k, within each LA, i.

The simulated distributions of population estimates are used to select an empirical 95% uncertainty for the true population size. The uncertainty interval is defined by the 2.5th and 97.5th percentile of the 1,000 simulated estimates.

Width of uncertainty intervals

The relative width of an uncertainty interval (UI) is calculated as 100*(upper bound – lower bound)/ABPE. The larger uncertainty interval widths are a direct result of the larger group standard deviations.

Figures 6a and 6b show the relative width of uncertainty intervals by age for local authorities in the normal clusters, for females and males, respectively. Figures 6c and 6d show the equivalent results for local authorities in the outlier clusters. They show that the intervals are larger and more variable in the outlier clusters than in the normal clusters. This is because the outlier clusters contain local authorities whose scaling factor patterns vary greatly within cluster, and therefore the observed standard deviations are large. Uncertainty is typically higher for males than for females. Uncertainty varies by age, typically highest for student and young adult ages.

Figure 6a: Relative widths of the uncertainty intervals by age, for females - normal clusters (1 to 4)

England and Wales, 2011

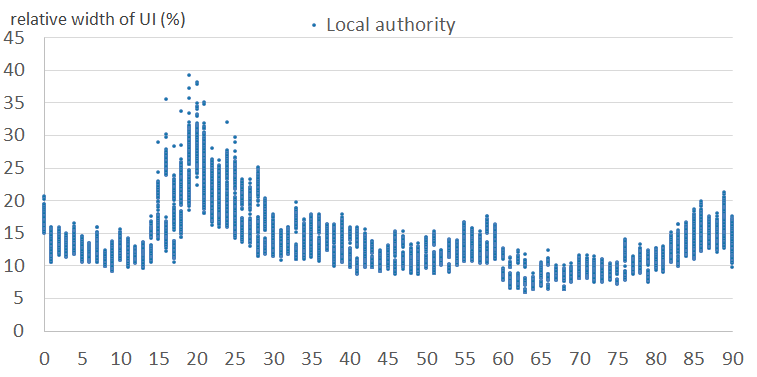
Source: Office for National Statistics

Download this image Figure 6a: Relative widths of the uncertainty intervals by age, for females - normal clusters (1 to 4)

.png (35.9 kB)

Figure 6b: Relative widths of the uncertainty intervals by age, for males - normal clusters (6 to 10)

England and Wales, 2011

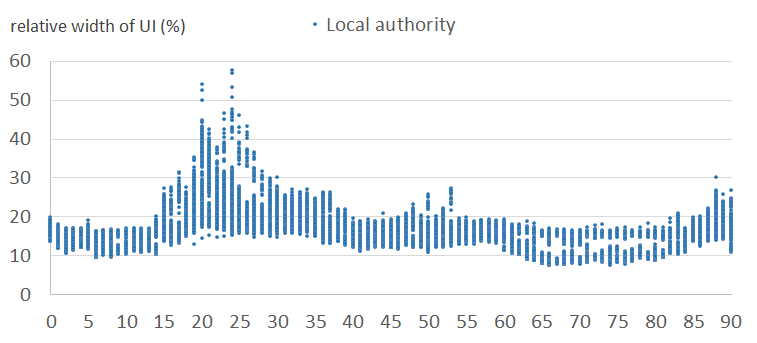
Source: Office for National Statistics

Download this image Figure 6b: Relative widths of the uncertainty intervals by age, for males - normal clusters (6 to 10)

.png (34.1 kB)

Figure 6c: Relative widths of the uncertainty intervals by age, for females - outlier cluster (5)

England and Wales, 2011

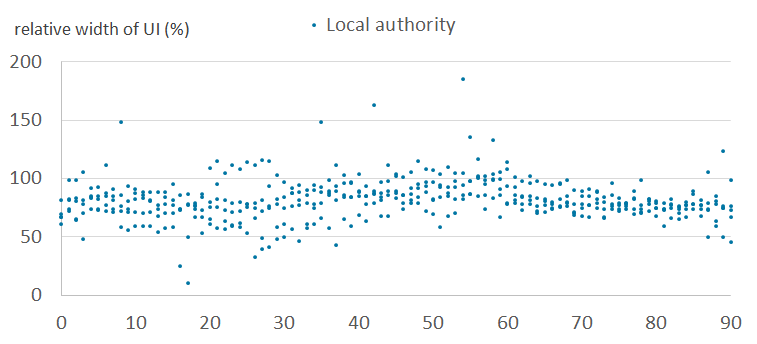
Source: Office for National Statistics

Download this image Figure 6c: Relative widths of the uncertainty intervals by age, for females - outlier cluster (5)

.png (15.4 kB)

Figure 6d: Relative widths of the uncertainty intervals by age, for males - outlier cluster (11)

England and Wales, 2011

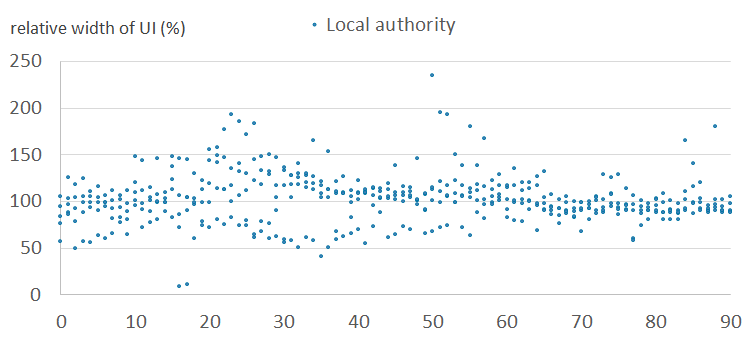
Source: Office for National Statistics

Download this image Figure 6d: Relative widths of the uncertainty intervals by age, for males - outlier cluster (11)

.png (16.4 kB)

Location of the ABPEs in their uncertainty intervals

We find that 15,689 (25%) ABPEs in the normal clusters and 69 (7.5%) in the outlier clusters lie outside their uncertainty interval (UI). This occurs when the middle 95% of the simulated scaling factors do not include 1. For them to contain 1, the corresponding simulated LSFs must contain 0 (log(1) = 0), and this can only happen if σ is large enough to extend the distribution sufficiently far out from the observed LSF. The census estimate always lies inside the uncertainty interval.

Figure 7a shows the distribution of the positions of the published ABPEs in their uncertainty intervals. The position is calculated as

where L is the lower bound of the uncertainty interval, and U is the upper bound. Therefore, a position of negative 1 means that the ABPE is the lower bound of the uncertainty interval, 0 means that the ABPE lies in the centre, and 1 means that the ABPE is the upper bound.

Figures 7b and 7c show how often the ABPEs fall outside of their uncertainty intervals for each age, by sex. The ABPEs fall outside most frequently for males aged 20 years, of working age, and from age 30 years to retirement, for both sexes.

Figure 8 shows that for males aged 25 to 31 years, and 43 to 64 years in Richmondshire, the ABPE falls outside the 95% uncertainty interval.

Notes for Uncertainty intervals

1. This assumption is supported by statistical testing of distributional differences using the two-sample Kolmogorov-Smirnof test, with Bonferroni correction for multiple comparisons.

2. The 1,000 resampled residuals are added to the observed LSFs as opposed to the fitted LSFs. This is because observed LSF values reflect relatively stable structural characteristics of LAs that are likely to persist over time.

The ABPE uncertainty intervals currently assume that bias in the ABPEs is unchanged as the decade following the census progresses. The inclusion of contemporaneous covariates would allow us to update the model, to account for change in the ABPE/Census relationship over time.

Explore the effects of clustering on the uncertainty intervals, including varying K (the pre-determined number of clusters), using hierarchical clustering, and choosing a subset of ages on which to base the clustering.

We also propose that further work could look at local authority-level analysis of the statistical uncertainty (as shown in Figure 8) and how it varies over time, place, and demographic group.

1. Import Census and ABPE estimates for each local authority (LA), i = 1, ... , 348 by sex, j = 1,2,and single year of age, k = 0, ... , 90(+).

2. Calculate the observed log-scaling factors (LSFs),

for all i,j,k

3. Identify unusual LAs separately for females and males based on the distance of their LSFs from the median LSFs and place them in two "outlier" clusters.

4. For each sex, cluster the remaining LAs based on similar patterns of LSFs across ages.

5. Fit a GAM to each cluster to obtain residuals, r_i,j,k.

6. For each combination of “normal” cluster, sex and age (group), calculate the standard deviation of the residuals, σ_c,j,k.

7. For normal clusters, calculate the standardised residuals, s_i,j,k, by dividing each of the residuals, r_i,j,k, by their group standard deviation, σ_c,j,k, i.e.

8. Put the standardised residuals into ”Pot 1”.

9. Resample 1,000 standardised residuals (with replacement) from Pot 1.

10. For each group in the normal clusters, un-standardise the selected residuals by multiplying the selected residuals by the group standard deviation, σ_c,j,k.

11. Put the raw residuals from the female outlier cluster into “Pot 2”, and those from the male outlier cluster into “Pot 3”.

12. For each group in the female (male) outlier cluster resample 1,000 residuals (with replacement) from Pot 2 (3).

13. For each group in all clusters, add the 1,000 residuals to the observed LSFs, lsf_i,j,k, to generate 1,000 simulated LSFs for each LA.

14. To obtain a simulated distribution of population estimates for each LA by age and sex, exponentiate the 1,000 simulated LSFs (generating 1,000 plausible scaling factors), and then multiply each of them by the published ABPE.

15. For each LA by age and sex, use the simulated distribution of population estimates to calculate the uncertainty interval as follows: the lower and upper limits of the uncertainty intervals are the 2.5th and 97.5th percentile of the 1,000 simulated estimates.

Cluster 1 (females) 86 LAs

Adur, Allerdale, Arun, Ashford, Babergh, Barnet, Bath and North East Somerset, Brighton and Hove, Broadland, Broxtowe, Cambridge, Camden, Canterbury, Ceredigion, Charnwood, Cheshire East, Chichester, Chiltern, Christchurch, Colchester, Conwy, Cornwall, Cotswold, Craven, Daventry, Derbyshire Dales, East Devon, East Dorset, East Hampshire, East Riding of Yorkshire, Eastbourne, Eden, Epping Forest, Forest of Dean, Fylde, Guildford, Gwynedd, Hambleton, Hammersmith and Fulham, Hart, Isle of Anglesey, Isle of Wight, Kingston upon Thames, Maldon, Malvern Hills, Mendip, Merton, Mid Devon, New Forest, Newark and Sherwood, North Kesteven, North Norfolk, Poole, Purbeck, Rochford, Rother, Runnymede, Scarborough, Selby, Shepway, South Hams, South Holland, South Kesteven, South Lakeland, South Northamptonshire, South Oxfordshire, Stratford-on-Avon, Stroud, Suffolk Coastal, Surrey Heath, Swale, Tewkesbury, The Vale of Glamorgan, Torridge, Vale of White Horse, Welwyn Hatfield, West Berkshire, West Devon, West Dorset, West Lindsey, West Somerset, Winchester, Wokingham, Wychavon, Wyre, York

Cluster 2 (females) 74 LAs

Barking and Dagenham, Barrow-in-Furness, Bedford, Blackpool, Bolton, Boston, Bournemouth, Brent, Burnley, Cardiff, Carlisle, Castle Point, Cheshire West and Chester, Corby, County Durham, Coventry, Denbighshire, Ealing, East Lindsey, Exeter, Fenland, Great Yarmouth, Haringey, Harlow, Hartlepool, Hillingdon, Hounslow, Hyndburn, Islington, Knowsley, Lancaster, Leeds, Leicester, Lewisham, Lincoln, Liverpool, Luton, Mansfield, Merthyr Tydfil, Middlesbrough, Newcastle upon Tyne, Newham, Newport, North Devon, North Somerset, Northampton, Norwich, Nottingham, Oxford, Peterborough, Plymouth, Preston, Reading, Redcar and Cleveland, Rhondda Cynon Taf, Sandwell, Sefton, Solihull, Southampton, St. Helens, Stoke-on-Trent, Sunderland, Swansea, Tameside, Teignbridge, Tendring, Thanet, Torbay, Tower Hamlets, Waltham Forest, Wellingborough, West Lancashire, Weymouth and Portland, Wolverhampton.

Cluster 3 (females) 121 LAs

Amber Valley, Ashfield, Barnsley, Basildon, Basingstoke and Deane, Bassetlaw, Bexley, Birmingham, Blaby, Blackburn with Darwen, Blaenau Gwent, Bolsover, Bradford, Breckland, Bridgend, Bristol, City of, Bromley, Bromsgrove, Broxbourne, Bury, Caerphilly, Calderdale, Cannock Chase, Carmarthenshire, Central Bedfordshire, Chelmsford, Chesterfield, Chorley, Copeland, Crawley, Croydon, Darlington, Dartford, Derby, Doncaster, Dudley, East Staffordshire, Enfield, Erewash, Flintshire, Gateshead, Gedling, Gloucester, Gosport, Gravesham, Greenwich, Hackney, Halton, Harrow, Hastings, Havant, Havering, Hertsmere, High Peak, Hinckley and Bosworth, Ipswich, Kettering, King's Lynn and West Norfolk, Kingston upon Hull, City of, Kirklees, Lambeth, Lichfield, Manchester, Medway, Milton Keynes, Neath Port Talbot, Newcastle-under-Lyme, North East Derbyshire, North East Lincolnshire, North Hertfordshire, North Tyneside, North Warwickshire, North West Leicestershire, Northumberland, Nuneaton and Bedworth, Oadby and Wigston, Oldham, Pendle, Portsmouth, Redbridge, Redditch, Rochdale, Rossendale, Rotherham, Rugby, Rushmoor, Salford, Sedgemoor, Sheffield, Slough, South Gloucestershire, South Ribble, South Somerset, South Tyneside, Southend-on-Sea, Southwark, Spelthorne, Stevenage, Stockport, Stockton-on-Tees, Sutton, Swindon, Tamworth, Taunton Deane, Telford and Wrekin, Thurrock, Torfaen, Trafford, Wakefield, Walsall, Wandsworth, Warrington, Warwick, Watford, Waveney, Wigan, Wirral, Worcester, Worthing, Wrexham, Wyre Forest.

Cluster 4 (females) 62 LAs

Aylesbury Vale, Bracknell Forest, Braintree, Brentwood, Cheltenham, Cherwell, Dacorum, Dover, East Cambridgeshire, East Hertfordshire, East Northamptonshire, Eastleigh, Elmbridge, Epsom and Ewell, Fareham, Harborough, Harrogate, Herefordshire, County of, Horsham, Huntingdonshire, Lewes, Maidstone, Melton, Mid Suffolk, Mid Sussex, Mole Valley, Monmouthshire, North Dorset, North Lincolnshire, Pembrokeshire, Powys, Reigate and Banstead, Ribble Valley, Richmond upon Thames, Richmondshire, Rushcliffe, Rutland, Ryedale, Sevenoaks, Shropshire, South Bucks, South Cambridgeshire, South Derbyshire, South Norfolk, South Staffordshire, St Albans, St Edmundsbury, Stafford, Staffordshire Moorlands, Tandridge, Test Valley, Three Rivers, Tonbridge and Malling, Tunbridge Wells, Uttlesford, Waverley, Wealden, West Oxfordshire, Wiltshire, Windsor and Maidenhead, Woking, Wycombe.

Cluster 5 (females) 5 LAs

City of London, Forest Heath, Isles of Scilly, Kensington and Chelsea, Westminster.

Cluster 6 (males) 73 LAs

Aylesbury Vale, Barnet, Braintree, Breckland, Brentwood, Bromley, Bromsgrove, Chelmsford, Cheltenham, Chorley, Christchurch, Craven, Dacorum, Dartford, Derbyshire Dales, Dover, East Hertfordshire, Eastleigh, Eden, Epping Forest, Epsom and Ewell, Hambleton, Harborough, Harrogate, Hart, Herefordshire, County of, High Peak, Huntingdonshire, Isle of Wight, Lewes, Lichfield, Mid Suffolk, Mid Sussex, Mole Valley, Monmouthshire, North Dorset, North Hertfordshire, Pembrokeshire, Powys, Reigate and Banstead, Richmond upon Thames, Richmondshire, Rochford, Rushcliffe, Sevenoaks, Shepway, Shropshire, South Bucks, South Derbyshire, South Oxfordshire, South Staffordshire, Spelthorne, St Albans, St Edmundsbury, Stafford, Staffordshire Moorlands, Surrey Heath, Sutton, Tandridge, The Vale of Glamorgan, Three Rivers, Thurrock, Tonbridge and Malling, Tunbridge Wells, Uttlesford, Warwick, Wealden, West Devon, West Oxfordshire, Westminster, Wiltshire, Windsor and Maidenhead, Wycombe.

Cluster 7 (males) 80 LAs

Barking and Dagenham, Barrow-in-Furness, Bedford, Birmingham, Blackburn with Darwen, Blackpool, Bolton, Boston, Brent, Burnley, Bury, Cambridge, Cardiff, Cheshire West and Chester, Corby, County Durham, Coventry, Crawley, Derby, Ealing, East Lindsey, Exeter, Fenland, Great Yarmouth, Halton, Harlow, Hartlepool, Hillingdon, Hounslow, Hyndburn, Kingston upon Hull, City of, Knowsley, Lancaster, Leeds, Leicester, Lincoln, Luton, Mansfield, Merthyr Tydfil, Middlesbrough, Newcastle upon Tyne, Newham, Newport, North East Lincolnshire, North Somerset, Northampton, Norwich, Nottingham, Nuneaton and Bedworth, Oxford, Peterborough, Plymouth, Preston, Reading, Redcar and Cleveland, Rhondda Cynon Taf, Rochdale, Rotherham, Salford, Sandwell, Scarborough, Sefton, South Holland, South Tyneside, Southampton, St. Helens, Stoke-on-Trent, Sunderland, Tameside, Tendring, Thanet, Torbay, Wakefield, Waveney, Wellingborough, Welwyn Hatfield, West Lancashire, West Lindsey, Wirral, Wolverhampton.

Cluster 8 (males) 20 LAs

Bridgend, Bristol, City of, Enfield, Gloucester, Hackney, Hammersmith and Fulham, Haringey, Havering, Islington, Lambeth, Lewisham, Liverpool, Manchester, Merton, Neath Port Talbot, Rushmoor, Southwark, Tower Hamlets, Waltham Forest, Wandsworth.

Cluster 9 (males) 70 LAs

Adur, Arun, Ashford, Babergh, Basingstoke and Deane, Bath and North East Somerset, Bournemouth, Broadland, Camden, Canterbury, Central Bedfordshire, Ceredigion, Charnwood, Cheshire East, Chichester, Chiltern, Conwy, Cornwall, Cotswold, Daventry, East Cambridgeshire, East Dorset, East Hampshire, East Northamptonshire, East Riding of Yorkshire, Elmbridge, Fareham, Forest of Dean, Fylde, Guildford, Gwynedd, Horsham, Kingston upon Thames, Maidstone, Maldon, Malvern Hills, Melton, Mendip, Mid Devon, New Forest, North Lincolnshire, North Norfolk, North West Leicestershire, Poole, Ribble Valley, Rother, Runnymede, Ryedale, South Cambridgeshire, South Hams, South Kesteven, South Lakeland, South Norfolk, South Northamptonshire, Stratford-on-Avon, Stroud, Suffolk Coastal, Swale, Teignbridge, Test Valley, Tewkesbury, Torridge, Waverley, West Berkshire, West Dorset, West Somerset, Winchester, Woking, Wokingham, Wychavon.

Cluster 10 (males) 100 LAs

Allerdale, Amber Valley, Ashfield, Barnsley, Basildon, Bassetlaw, Bexley, Blaby, Blaenau Gwent, Bolsover, Bracknell Forest, Bradford, Brighton and Hove, Broxbourne, Broxtowe, Caerphilly, Calderdale, Cannock Chase, Carlisle, Carmarthenshire, Castle Point, Cherwell, Chesterfield, Colchester, Copeland, Croydon, Darlington, Denbighshire, Doncaster, Dudley, East Devon, East Staffordshire, Eastbourne, Erewash, Flintshire, Gateshead, Gedling, Gosport, Gravesham, Greenwich, Harrow, Hastings, Havant, Hertsmere, Hinckley and Bosworth, Ipswich, Isle of Anglesey, Kettering, King's Lynn and West Norfolk, Kirklees, Medway, Milton Keynes, Newark and Sherwood, Newcastle-under-Lyme, North Devon, North East Derbyshire, North Kesteven, North Tyneside, North Warwickshire, Northumberland, Oadby and Wigston, Oldham, Pendle, Portsmouth, Purbeck, Redbridge, Redditch, Rossendale, Rugby, Sedgemoor, Selby, Sheffield, Slough, Solihull, South Gloucestershire, South Ribble, South Somerset, Southend-on-Sea, Stevenage, Stockport, Stockton-on-Tees, Swansea, Swindon, Tamworth, Taunton Deane, Telford and Wrekin, Torfaen, Trafford, Vale of White Horse, Walsall, Warrington, Watford, Weymouth and Portland, Wigan, Worcester, Worthing, Wrexham, Wyre, Wyre Forest, York.

Cluster 11 (males) 5 LAs

City of London, Forest Heath, Isles of Scilly, Kensington and Chelsea, Rutland.