2. Introduction
Office for National Statistics (ONS) has been looking into alternative sources of data to supplement or replace existing data collection methods such as the use of surveys.
Currently the majority of ONS statistics are derived from carefully designed surveys. The research into other data sources is part of a programme to innovate and transform official statistics. These datasets fall into two categories, administrative data and found data.
Administrative data are data collected by governmental departments for non-statistical purposes, for example, ONS has been investigating using VAT turnover data to compile the UK National Accounts, (Edwards [2017]).
Found data are data whose main purpose is not necessarily the purpose it was created for. One example of this is the use of satellite imagery. This was originally created to aid mapping but now it is also being used for land use statistics.
These administrative and found data are also useful in the construction of price statistics. Administrative data have been used in the Producer Price Index (for example, prices for home-produced foods come from the Department for Environment, Food and Rural Affairs (ONS [2014b]), and in the Services Producer Price Index (for example, a Business Rail fares index is supplied to ONS by Office of Rail and Road (ONS [2015]). On the consumer prices side there are two found data sources that can be used in the compilation of Consumer Prices Indices. These two sources are transactions or scanner data and web scraped.
Scanner data are the data on sales of products bought by consumers at the point of sale. These data then contain both the quantities of the good bought and the prices at which the customers bought the good. These data aren't collected for the purpose of price statistics; it is often kept for stock-keeping reasons. Scanner data could also contain other information that is useful, such as characteristics of the products.
Scanner data also has the added benefit of allowing the use of weights at the lowest level of aggregation, the so-called elementary aggregate level. Currently in the Consumer Prices Index including owner occupiers’ housing costs (CPIH) at the elementary aggregate level there are no weights used to aggregate individual product price relatives together. For example, the total household expenditure on apples in the UK is used in the CPIH to weight the prices of apples together with other items in the basket of goods and services to form the aggregate measure. However, when measuring the price changes for apples specifically, the expenditure on Pink Lady apples bought in Cardiff from a multiple shop1 is not known, and therefore all apple products are weighted equally together at the elementary aggregate level. Scanner data would allow for this information, if the retailer keeps it at this level of disaggregation.
Scanner data also gives us more detail than just quantities; it gives us a larger set of products and possibly a larger geographic coverage than the current CPIH data collection method, which prices a sample of around 700 representative items at a sample of outlets from a sample of 140 locations across the country. Scanner data also has the potential to be of a higher frequency than the current collection, as weekly or possibly daily prices and quantities could be observed, giving more information to be used in the CPIH.
However, other aspects of coverage may be an issue for scanner data. It is likely that scanner data would only be obtained for larger stores and wouldn't be available for small stores such as corner shops. In addition, not all the areas of the CPIH basket would be covered by scanner data. For example, the fees charged by plumbers, electricians, carpenters and decorators are collected as part of the CPIH collection. It wouldn’t be possible to collect scanner data for this item as most of the providers of these services wouldn’t collect these data and there would be too many providers to ask to get a reasonable coverage.
Currently, ONS does not have access to scanner data. However, other national statistics institutes (NSIs) have been using it to compile their Consumer Prices Indices for a number of years. Statistics New Zealand, (Bentley and Krsinich [2017]), have been using scanner data in the technological goods part of the basket. The Australian Bureau of Statistics has since 2014 included scanner data for 25% of their CPI. Statistics Netherlands has been using scanner data since 2002, (de Haan and van der Grient [2009]), and now make use of it for many areas of their basket. As of 2017, it is to the best of the author’s knowledge that the following European countries use scanner data in their CPIs: Norway, (Johansen and Nygaard [2012]), Sweden, (Sammar et al. [2012]), Switzerland, (Müller [2010]), Iceland, (Guđmundsdótti and Jónasdóttir [2014]), and Belgium, (Statistics Belgium [2016]). INSEE, the NSI of France, have plans to implement scanner data after a change of legislation (Rateau [2017]).
Another found data source that can be used in the compilation of consumer price statistics is web scraped data. Web scrapers can be defined as software tools, which are used for extracting data from web pages. Web scraped prices data are collected by scraping retailers’ websites to get price and other attribute information on products.
Web scraped data has similar advantages to scanner data in terms of product coverage and frequency, but also has a number of disadvantages as well. One disadvantage is that products with very low expenditure may still be scraped (for example, products which have not been bought recently by consumers). This means that products could be included in the index which aren't representative of consumer spending. Web scraping is also only restricted to those retailers with an online presence. These are usually medium to large retailers, not small retailers; a similar constraint to the use of scanner data. Even for medium to large retailers, not all will have a website; for example, some discount retailers do not have a retail presence on their websites.
ONS has been exploring the use of web scraped data since 2014, and has published a number of research articles on the use of web scraped grocery data (Breton et al. [2015] and Breton et al. [2016]). The web scraped data are often of a higher frequency and volume than traditionally collected price data. For example, the ONS traditional collection for the 33 CPIH items that are currently included in the grocery web scraping pilot is 6,000 price quotes a month whereas the web scrapers collect 8,000 price quotes per day.
Other countries have also been investigating the use of web scraping in the calculation of consumer prices statistics. For example, the Netherlands, (Chessa and Griffioen [2016]), for clothing data; New Zealand, (Bentley and Krsinich [2017]), for varied areas of the basket; Italy, (Polidoro et al. [2015]), for airfares and consumer electronics; and Germany for flights, hotels, mail order selling (mainly clothing and footwear), mail order pharmacies, hire cars, train travel and city breaks, (Brunner [2014]). The Federal Statistics Office of Germany has also been looking into web scraping to examine dynamic pricing (Blaudow and Burg [2017]).
From this ongoing research into these alternative data sources, it has become clear that traditional methods of compiling consumer price statistics may not be able to cope with both the frequency and volume of these new data, therefore new methodology is required. Chessa and Griffioen [2016], have compared indices for scanner data. Breton et al. [2016] details some of these methodologies (with a particular focus on web scraped data) and Metcalfe et al. [2016] describes new methodology to compile price indices from these data.
This article will assess these new methods for use on web scraped data using the criteria of the different approaches to index number theory. In index number theory there are many ways to derive and assess which methodology is suitable, three of those approaches will be used here. These are as follows:
- the axiomatic approach (see International Labour Organisation (ILO) consumer price index manual chapter 16) – the index is tested against some desirable properties
- the economic approach (see ILO consumer price index manual chapter 18) – the index is ranked against whether or not it approximates or is exact for a Cost of Living index
- the statistical (Stochastic) approach (see ILO consumer price index manual chapter 16) – each price change is an observation of population value of inflation and the index is the point estimate of inflation
Notes for: Introduction
- A multiple shop is a shop which has 10 or more stores in a region.
3. Price index methods for use on web scraped prices data
3.1 Introduction
In index number theory there are many different price indices that have been formulated to measure price changes. These can be split into weighted and un-weighted formulae, depending on whether quantities have been observed with the prices. For example, the Jevons index is an unweighted index whereas the Laspeyres index is a weighted index.
Price indices can also be divided into bilateral and multilateral indices. Bilateral indices only compare two periods with each other to measure price change while multilateral indices compare three or more periods. For web scraped data, this means that only indices that are classed as un-weighted should be assessed (although weight proxies could be used if weighted indices are desired; this is left to future research), and both bilateral and multilateral indices can be included.
The following indices have been used to calculate price indices from web scraped data:
- bilateral indices
- Fixed Base Jevons (this was called the “unit price” index in our previous releases)
- Chained Bilateral Jevons (this was called the “daily chained” index in our previous releases)
- Unit Value
- Clustering Large datasets into Price Indices (CLIP)
- multilateral indices
- the GEKS family of indices; all the GEKS methods in this article use Jevons indices as an input into the GEKS procedure (GEKS-J)1
- the Fixed Effects index with a Window Splice (FEWS)
- the Gheary-Khamis index
All of these indices, with the exception of the Fixed Based Jevons, aim to overcome the inherent problem in both web scraped and scanner data of product churn (Definition 3.1). This is done mainly through frequent chaining. The FEWS index also tries to adjust for the quality changes (Definition 3.2), which occur due to product change.
Definition 3.1 [Product churn]
Product churn is the process of products leaving and/or entering the sample.
Products can leave or enter the sample in one of five ways:
- product goes out of stock, temporally leaves the sample
- product is restocked, and re-enters the sample
- product is discontinued and permanently leaves the sample
- product is new to the market
- product is rebranded
Example 3.1 [Product churn]
Figure 1: Product churn example

Source: Office for National Statistics
Download this image Figure 1: Product churn example
.png (23.3 kB) .xlsx (9.8 kB)Figure 1 shows an example of product churn. Only one product remains in the sample for all 10 periods, product 3. Three products start in stock then go out of stock and then return in stock at different frequencies. Product 2 goes out of stock permanently. Products 7, 8, 9 and 10 are new to the market, but 8 goes out of stock to be replaced by product 9. Product 10 appears for one period only.
Figure 2: Product churn in apples from June 2014 to March 2017 coloured by store
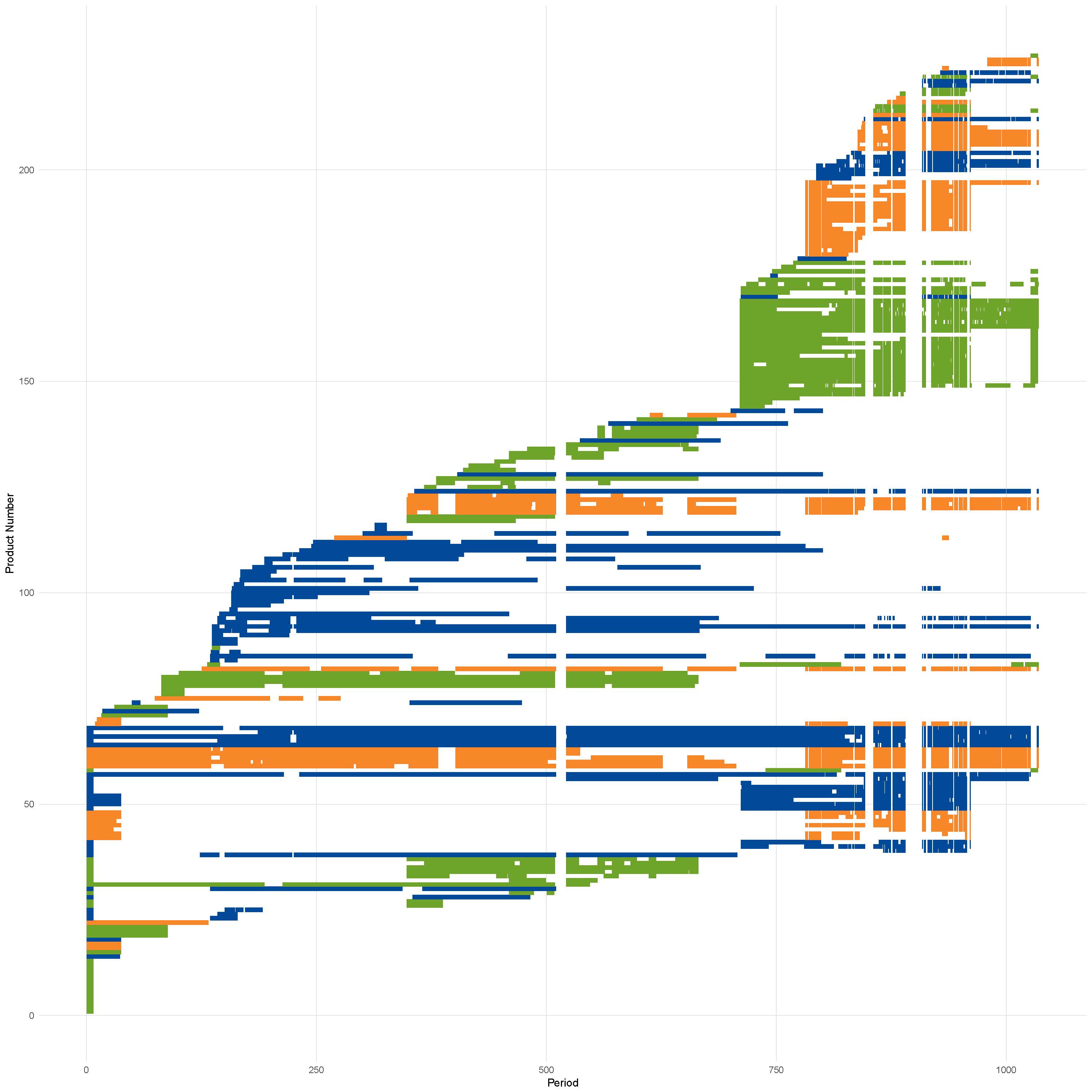
Source: Office for National Statistics
Notes:
- Areas of where all products have no values is due to scraper breaks not product churn.
Download this image Figure 2: Product churn in apples from June 2014 to March 2017 coloured by store
.png (384.1 kB) .xlsx (5.8 MB)Figure 2 shows the product churn in apples data collected by Office for National Statistics (ONS) web scrapers. There is no product that exists in all time periods in the dataset, even if scraper breaks2 are discounted.
Definition 3.2 [Quality change]
Products only exist in an unchanged form for a period of time. When a product is discontinued, often it is replaced with a "new and improved" model. This improvement is called a quality change.
Example 3.2
If a laptop is discontinued and replaced with a new model with a larger hard drive in the next time period then there has been a quality change between the two products. Therefore, any price change observed between the two periods may be attributed to quality change, rather than pure price change, which is what a price index is intended to capture. It is therefore important to account for quality change when constructing price indices.
3.2 Fixed Based Jevons
The Fixed Based Jevons fixes the base period to the first period in the dataset, and matches the products common to all periods. This is the main method used in constructing the elementary aggregates in the Consumer Prices Index including owner occupiers’ housing costs (CPIH). It compares the current period price back to the base period. The formula is defined as follows:
where ptj is the price of product j in time period t, S* is the set of all products that appear in every period and n*=∣ S*∣ is the number of products common to all periods.
The Fixed Based Jevons index will suffer in markets where there is high product churn. This is because when you get further away from the base period, the less likely it is that products are going to remain in the sample. A practical example is women's coats where at the end of each "season" the whole stock can be phased out in certain retailers and replaced with the new season's stock, (Payne [2017]). For cases when this occurs, that is, S*=∅ then an index cannot be calculated. For this reason, the base period is changed each January to allow for changes in the products available to consumers and for more matches to occur. These within-year indices are then linked together. This happens in both the web scraped data and in the CPIH.
The advantages of the Fixed Based Jevons include the fact that there is a direct comparison from the base period to the current period and that it tracks individual products across time. It is also relatively straightforward and easy to explain, and follows the methodology that is currently used in CPIH.
3.3 Chained Bilateral Jevons
The Chained Bilateral Jevons index involves constructing Bilateral Jevons indices between period t and t-1 and then chaining them together. The formula is defined as follows:
where PJi-1,i is the Jevons index between the current period and the previous period, pji is the price of product j at time i, Si-1,i is the set of products observed in both period i and i-1, and ni-1,i is the number of products in Si-1,i.
The Chained Bilateral Jevons index uses more data than the Fixed Based Jevons because products only need to exist in contiguous periods to be included in the index. It has other advantages in a production environment as it only needs the current and previous period data to calculate the index, compared with some of the other methodologies, which require more of the historical data. The index is also computationally straight forward, and easy to explain. Disadvantages to the Chained Bilateral Jevons index include the fact that the index isn't being directly compared to the base period, and there is a possibility of chain drift. Using the notation of Clews et al. [2014], chain drift is defined as follows:
Definition 3.3 [Chain drift]
Let f(a,b) be an arbitrary index formula. Then a direct index Λ between 0 and 2 is defined as follows:
A linked index Λ* is defined as:
Then chain drift is defined as the difference between the chained index and the direct index, that is:
This can also be restated as the chained index not equalling the direct index.
Proposition 3.1
The Chained Bilateral Jevons index exhibits chain drift if there exists product churn in the dataset.
Let f in Definition 2.1 be the Jevons index, then Λ is the Fixed Based Jevons index and Λ* is the Chained Bilateral Jevons. Then there are four conditions depending on product churn, which are as follows:
If S0,1 = S1,2 = S* (that is, there is no product churn) then:
Therefore, there is no chain drift under this condition.
If S0,1 ≠ S1,2, n0,1 = n1,2 and S0,1 ∩ S1,2 = S* ≠∅, (that is, there is product churn but the amount of items that have disappeared are replaced with the same amount of new products, and not all products have disappeared), then:
Therefore, if there is product churn that keeps the number of products on the market constant over time then there exists some chain drift.
If S0,1 ≠ S1,2, n0,1 ≠ n1,2 and S0,1 ∩ S1,2 = S* ≠∅ (that is, products are churning but the number of products going out of stock aren't being replaced by the same amount of new products), then:
where
and
Therefore, in this type of product churn there is chain drift.
Finally, if S0,1 ≠ S1,2 and S0,1 ∩ S1,2 =∅ (that is, all products are replaced) then:
This means that as none of the prices cancel out, so there is product churn.
For a proof of all four conditions please see Appendix A.
Figure 3: Chain drift for the different types of product churn in Proposition 2.1
Source: Office for National Statistics
Download this chart Figure 3: Chain drift for the different types of product churn in Proposition 2.1
Image .csv .xlsFigure 3 shows the chain drift for different conditions. These are the averages of multiple simulations of prices randomly generated as follows:
For condition 2, the percentage overlap is the amount of products that appear in all three periods; for condition 3 the percentage indicates how much larger or smaller the number of products is in the second comparison compared with the first. It can be seen that the direction and magnitude of the chain drift is dependent on the different conditions.
3.4 Unit Value index
The Unit Value index is normally defined as the ratio of the unit value3 in the current period to the unit value in the base period. However, there is no quantity data in the web scraped data so a true Unit Value index can't be calculated. Instead the ratio of geometric means of unmatched sets of products will be used, that is:
where S0 is the set of products in period 0, and n0 is the number of products in S0, St is the set of products in period t, and nt is the number of products in St. The geometric mean has been used so that it is consistent with the other indices presented in this article. This is instead of an arithmetic mean, which would have fallen out if all the products had quantities equal to 1 (equivalent to a Dutot index).
3.5 Clustering Large dataset Into Price indices (CLIP)
A recent price index developed by ONS is the CLIP, (Metcalfe et al. [2016]). The CLIP takes a slightly different approach to forming an index in that instead of following individual products over time like the previous indices, it follows a group of products over time instead. This method attempts to overcome the product churn issue mentioned earlier when tracking individual products over time.
As the CLIP tracks groups of products over time, it allows for more of the data to be used as individual products do not need to be matched over time. This means that even if a product only appears in one period then it will still be included in the index.
The groups are found in a two-step process. First, the data from the base period is clustered to form the initial groups. The clustering method used is the mean shift algorithm. This fits a kernel over the characteristics, (such as product name, shop, offer and price), and then finds the nearest local maximum to the current point to be clustered. Once the clusters have been found, they are fixed and a decision tree is used to find the underlying rules that make up each cluster (here price is removed as a characteristic). New data are then parsed through the tree when it is observed in each new period and put into a particular cluster.
Following this, the geometric mean of the prices for each product in that cluster is taken to be the price for that cluster. The current price is then compared back to the base price for that cluster and then the resulting price relatives for each cluster are aggregated together arithmetically using weights calculated as follows:
where wi0 is the weight for cluster i and Ci is cluster i.
An advantage of using the clustering is that it allows for substitution when products go out of stock. For example; for apples, if in the base period Royal Gala, Pink Lady and Braeburn apples are placed in the same cluster, and in the next period Pink Lady apples go out of stock, the consumer might substitute to another item within the cluster. This is because the products within each cluster will have similar characteristics and the consumers might be indifferent to those characteristics. The CLIP therefore captures the price change for similar products as a group whereas other methods capture individual price change (and therefore can be more affected when these individual products leave the data).
3.6 The Gini, Eltetö, Köves and Szulc (GEKS) family of indices
The GEKS index was devised as a possible solution to calculating multilateral indices over domains that have no natural order. It is often used when calculating purchasing power parities (PPPs), where the domain of interest is countries; countries don’t have a natural ordering. The basic premise of a GEKS index is that it is an average of the bilateral indices for all combinations of comparisons of the domain units. Using PPPs as an example, if the countries of interest are {UK, USA, Germany} then the combinations are UK-Germany, UK-USA and Germany-USA.
3.6.1 The GEKS-J index
The GEKS index was adapted for the time domain by Ivancic et al. [2011]. As the authors had access to scanner data, they were able to use Fisher indices to calculate the bilateral component indices. However, as web scraped data does not have expenditure information, this article uses Jevons indices instead. This means that the GEKS-J price index for period t with period 0 as the base period is the geometric mean of the chained Jevons price index between period 0 and period t with every intermediate point ( i =1,..., t -1 ) as a link period. The formula is defined as follows:
A product is included in the index if it is in the period i and either period 0 or period t.
There are some problems with using a GEKS-J index. In later periods, there is a loss of characteristicity4 when the index involves price movements over large periods. That is, if a product is available in the base period and the comparison period i such that i is 2 years or more from the base period, then this price movement will be included in the index; this price movement is less relevant than a price movement from the previous month or week to the comparison period. The GEKS also does not adjust for the quality changes available on new products, or improvements on existing ones.
3.6.2 The Rolling Year GEKS-J index (RYGEKS-J)
The Rolling Year GEKS-J or RYGEKS-J is an extension of GEKS-J that accounts for this loss of characteristicity, and was first devised by de Haan and van der Grient [2009]. For a RYGEKS-J, after the initial window period, recent movements are then chained on to the previous movements as follows:
Here d is the window length. The optimal window length is still subject to discussion in the international community. For example, de Haan and van der Grient [2009] suggest 13 months should be used for monthly data, as this allows for the comparison of products that are strongly seasonal. The Australian Bureau of Statistics has adopted a 9-quarter window as their work shows that this is a better solution for seasonality, (Kalisch [2016]).
RYGEKS is preferable to a GEKS index due to this window. This is because it means that not all of the time series is required to calculate the current period index, and it also deals with the loss of characteristicity. The RYGEKS does lose transitivity but the effect of this is negligible.
3.6.3 Imputation Törnqvist RYGEKS - ITRYGEKS
As new products are introduced on the market and old products disappear, an implicit quality change may occur, for example, this often happens in technological goods. Hence, there is an implicit price movement which isn't captured in the standard RYGEKS method because it doesn’t account for quality change. There is an implicit price change when these goods are introduced, and if the consumption of these goods increased then these implicit movements need to be captured.
De Haan and Krsinich [2012] propose using an imputed Törnqvist as the base of the RYGEKS. An imputed Törnqvist is a hedonically adjusted Törnqvist index, where the prices of new or disappeared products are imputed using a hedonic regression in the base or current period respectively. A hedonic regression assumes that the price of a product is uniquely defined by a set of K characteristics. The imputed Törnqvist index is defined as follows:
where wj0 is the expenditure share of item j at time 0, wjt is the expenditure share for item j at time t, pjt is the estimated price for a missing product at time t, S0,t is the set of products observed in both periods, SN(0)t is the set of new products at time t but weren't available at time 0, and SD(t)0 is the set of products at time 0 that have disappeared from the market at time t. De Haan and Krsinich [2012] suggest three different imputation methods, these are:
The linear characteristics model:
This method estimates the characteristic parameters using a separate regression model for each period. The imputed price is calculated as follows:
where αt is the estimate of the intercept, βkt is the estimate of the effect characteristic k has on the price, and zjk is the value of characteristic k for product j.
The weighted time dummy hedonic method:
This method assumes parameter estimates for characteristics don't change over time, and includes a dummy variable, Dji, for in which period the product was collected. In this method the imputed price is calculated by:
The weighted time product dummy method:
This method can be used when detailed characteristic information is not available, and a dummy variable, Dj, for the product is created. The missing price is then estimated using:
where γj is the estimate of the product-specific dummy, and the Nth product is taken as the reference product. This method assumes that the quality of each distinct product is different to the quality of other products to a consumer. It is a reasonable assumption as the number of potential characteristics is large and not all of them are observable.
For each of these methods, a weighted least squares regression is used, with the expenditure shares as the weights. A disadvantage to using the ITRYGEKS especially with the linear characteristics and the time dummy methods is that they will give different results depending on what characteristics are placed in the model. De Haan et al. [2016] compare the differences between Time Dummy and Time Product Dummy indices. The results indicate that a time product dummy model has too many parameters, fits outliers and unduly raises the R2 compared with the underlying hedonic model. This then biases the out of sample predictions, the imputations in this case, meaning that the Time Product Dummy index is susceptible to quality change bias.
De Haan et al. [2016] decomposed the ratio between the time dummy and the time product dummy in terms of the residuals into three components as follows:
Here wD(t)0 is the aggregate weight of products that have disappeared by the current periods, wN(0)t is the aggregate weight of the new products, wMt is the aggregate weight of the items in both periods. u-0D(t)(TDH) is the weighted arithmetic mean of the residuals for the disappearing products using the time dummy model in period 0. u-0D(t)(TPD) being the equivalent for the time product dummy model. uM(TDH)-0(t) is a weighted arithmetic mean of the period 0 residuals but using the period t weights.
The first and second components are driven by the difference in the weighted average residuals in the disappearing and new products respectively, so if the difference is larger (in absolute value) there is a bigger disparity between the models. It also depends on the weights that each product has, so if there is a higher weight to the products that appear in both periods than to those that only appear in one period, the disparity would be smaller.
The third component depends on the normalised expenditures, and will generally be different from 1, this is because as a result of using the weighted least squares (WLS) time dummy technique are model-dependent. This term has the possibility of being larger when the weights of the matched product differ significantly, and will be equal to 1 in the situation where weights are constant over time. If an ordinary least squares (OLS) regression is used this term would always be equal to 1.
Due to weights not being observed at an individual product level, the WLS regressions discussed can’t be used and therefore OLS regression would be used to estimate the missing prices. In the ONS web scraped data there is limited characteristic data to produce a time dummy model therefore only the time product dummy method would be used. The Törnqvist would also be replaced with a Jevons due to the lack of weights, creating an IJRYGEKS (a Jevons version of the ITRYGEKS).
3.6.4 Intersection GEKS-J (IntGEKS-J)
The IntGEKS was devised by Lamboray and Krsinich [2015], to deal with an apparent flattening of RYGEKS under longer window lengths, although this was found later to be an error in applying the weights. It removes the asymmetry in the matched sets between periods 0 and i and between periods i and t, by including products in the matched sets only if they appear in all three periods, the set S0,i,t. The formula is defined as follows:
If there is no product churn then the IntGEKS-J reduces to the standard GEKS-J. The IntGEKS-J has more chance of "failing", that is, not being able to calculate an index, than a standard GEKS-J as the products need to appear in more periods. Using a Jevons as the base in the IntGEKS-J means that it then simplifies to an average of Jevons indices over differing samples. This is because the prices of the intermediate period i would cancel out in the calculation.
3.7 The Fixed Effects index with a Window Splice (FEWS)
The FEWS produces a non-revisable and fully quality-adjusted price index where there is longitudinal price and quantity information at a detailed product specification level, (Krsinich [2016]). It is based around the Fixed Effects index which is defined as follows:
where γ0 is the average of the estimated fixed effects regression coefficient at time 0. The Fixed Effects index is equivalent to a fully interacted5 Time Dummy index if the characteristics are treated as categorical. So if the product identifier, such as a barcode, changes when a price determining characteristics changes the fixed effects will equal a Time Dummy index (Krsinich [2016]). The Fixed Effects index is also equivalent to a Time Product Dummy index. Using a similar methodology to RYGEKS, the new series is spliced onto the current series for subsequent periods after the initial estimation window; this is called a window splice. The window splice is done as follows:
where P[0,d]0,1 is the index from period 0 to period 1 using the estimation window [ 0 , d ].
This approach has the advantage of incorporating implicit price movements of new products at a lag. However, this means that there is a trade-off between the quality of the index in the current period and in the long-term. Over the long-term, the FEWS method will remove any systematic bias due to not adjusting for the implicit price movements of new and disappearing items.
3.8 The Geary-Khamis index
The Geary-Khamis (GK) index was developed for PPPs, but unlike the GEKS, which compares each country to each other, the GK index compares each country to a standard country. It is an implicit price index that divides a value index by a weighted quantity index. Using similar notation to Chessa [2016] it is defined as:
where the weights vi are as follows:
The denominator essentially adjusts for quality, which is why this form of the Geary-Khamis index is also called a quality adjusted Unit Value index.
For the following analysis, the IntGEKS and the IJRYGEKS have been excluded. This is due to the former being an average of Fixed Based Jevons indices over different samples, and would have both the properties of the GEKS-J. The latter is just a different input index to a RYGEKS and should therefore have the same properties. The Geary-Khamis index is also excluded due to the current lack of a quantity proxy.
Notes for: Price index methods for use on web scraped prices data
- The IntGEKS-J was not included in the comparisons as it uses the same structure as GEKS-J but just includes a different set of products. The IJRYGEKS (a Jevons version of the ITRYGEKS) was also not included due to the lack of characteristics to perform the imputations required.
- A scraper break occurs when no data appears for all products due to a website redesign or a lab outage. For more information, please see Box 1 in Breton et al 2016.
- Unit value is defined as
- Characteristicity is the extent to which an index is based on relevant data.
- Fully interacted means that all possible interaction terms are included in the model, for example y=a+b+c is not fully interacted, neither is y=a+b+c+ab, which includes an interaction term, only y=a+b+c+ab+ac+bc+abc is fully interacted.
4. The test/axiomatic approach
The test/axiomatic approach to index numbers assesses the index number formulae against some desirable functional properties (axioms) an index should have. An index will either pass or fail each axiom. If an index passes all of the axioms, then it is deemed to perform well. However, it is important to note that different price statisticians may have different ideas about what axioms are important, and alternative sets of axioms can lead to the selection of different “best” index number formula. There is no universal agreement on what is the best set of reasonable axioms and therefore, the axiomatic approach can lead to more than one best index number formula.
The following definitions will be used throughout this section.
Let p0 and pt be the vector of prices observed at the period 0 and t respectively and let P ( p0 , pt ) be an arbitrary price index.
Axiom 1 [Positivity Test]
An index should be positive:
P ( p0 , pt )>0
All of the formulae satisfy Axiom 1. This is easy to show because all of the formulae involve a geometric mean, either of the prices or price relatives. The geometric mean is defined as:
Given that measured prices are always positive, the domain is restricted to R+n. This means that the co-domain is restricted to R+.
Further consideration is required of the Fixed Effects index with a Window Splice (FEWS) index because of the quality adjustment term. However, although the regression coefficients, their arithmetic mean and the difference between the two periods could all be negative, taking the exponential of the resulting difference makes it positive. This is because the exponential function maps R to R+.
Axiom 2 [Continuity Test]
P ( p0 , pt ) is a continuous function of its arguments
Axiom 2 is satisfied by all of the formulae. This is because all of the input functions (that is, arithmetic and geometric means and the exponential) are continuous, the sums and products of continuous functions are also all continuous, and therefore all of the price indices are continuous.
Axiom 3 [Identity/constant prices Test]
P ( p , p )=1
If the prices are constant then the index is 1
If there is no product churn in the data then all of the indices satisfy Axiom 3. However, if there is product churn then the FEWS, Unit Value and the Clustering Large datasets into Price Indices (CLIP) indices fail this axiom. It is worth noting that the CLIP only fails with respect to products rather than clusters (this is because the price of each cluster is constant).
The reason that the Jevons-based indices pass this axiom is that they require matched products to be included in the index and therefore unmatched products are excluded from the index. The FEWS, Unit Value and CLIP use unmatched products and therefore are affected by product churn. To see this, let S0 = { p1 , p2 , p3 } and S1 = { p1 , p3 } be the prices observed in period 0 and period 1 respectively. For the CLIP, Unit Value and the non-quality adjustment part of the FEWS, the following is obtained:
In general this is true but there are two special cases where the ratio is equal to 1:
- p1 = p2 = p3
- p2 = √ p1 p3.
For the quality adjustment factor part of the FEWS index, the difference of the arithmetic means of the fixed effects coefficients needs to equal zero for the Identity Test to be satisfied. However, when a product churns out of the dataset, this is unlikely to occur, as:
It is entirely possible that when a product churns out of the dataset, the coefficients for the other products will adjust to take account of this missing product. For the FEWS to pass this axiom both parts of the index must either be equal to 1 individually or they can be not equal to 1 but their product must be.
Figure 4 shows the effect of product churn on FEWS when all of the prices are constant. For each period 5% of the products were removed from the sample, taking a simple random sample without replacement. For most of the periods this removal of products decreases the index because the geometric mean of the current period will be smaller than for the base period. However, for some periods this increases the index, due to the quality adjustment factors over-adjusting for the change in quality due to the product churn.
Figure 4: The effect of product churn on the FEWS in the Identity Test, showing only the first 130 periods
Source: Office for National Statistics
Download this chart Figure 4: The effect of product churn on the FEWS in the Identity Test, showing only the first 130 periods
Image .csv .xlsAxiom 4 [Proportionality in Current Prices Test]
If all current prices are multiplied by λ then the new price index is λ times the original index, that is:
P ( p0 , λ pt ) = λ P ( p0 , pt )
Axiom 5 [Inverse proportionality in Base Prices Test]
If all base prices are multiplied by λ then the new price index is the original index divided by λ, that is:
P ( λ p0 , pt ) = P ( p0 , pt) / λ
All indices satisfy both Axioms 4 and 5; this is shown in the following proof for the Jevons index.
Proof
Let P ( p0 , pt ) be the Jevons index. Then it follows:
The same logic can be applied for base prices.
For the other indices, the same logic applies, for example in the CLIP the λ would be multiplied by itself ∣ Cit ∣ times within a cluster but then the ∣ Cit ∣ th root would be taken in each cluster and the λ would be taken out as a factor. The same happens for the Unit Value and the FEWS. This λ factor wouldn’t affect the quality adjustment factors as it would be absorbed into the coefficient of the time dummy for the current period, making it logλ larger.
For the GEKS, from each of the bilateral Jevons there is a λ, this is raised to the power of t+1 because of the t+1 comparisons from intermediate period i to current period t but since the geometric mean of all these comparisons is taken in the GEKS this becomes λ. In summary, product churn does not have an impact on this axiom, as it only affects n.
Axiom 6 [Commodity Reversal Test]
If the ordering of the products changes the price index stays the same, that is:
where A is a permutation matrix .
Due to the commutative property of addition and multiplication over the real numbers all of the indices pass the Commodity Reversal Test.
Axiom 7 [Invariance to the change in units/Commensurability Test]
P ( Dp0 , Dpt ) = P ( p0 , pt )
where D is a diagonal matrix with the conversion factors on the diagonal.
The CLIP, Unit Value and FEWS indices fail this test in the presence of product churn because the conversion factors do not cancel out in the unmatched means. Using the same two observation vectors that were used in the Identity Test (Axiom 3) along with the following conversion matrix, D = diag ( d1~,d~2~,d~3 ) the following happens:
As with Axiom 3, there are special cases where the geometric means of the conversion factors happen to be equal and where all the conversion factors are equal.
Axiom 8 [Time Reversal Test]
If the data for the base and current periods are interchanged then the resulting index is the reciprocal of the original one.
The RYGEKS, FEWS, and CLIP indices fail this test1. The RYGEKS index fails it due to the initial window before the chaining starts. This is because if there is price change in the window, the following happens:
GEKSJ0,d ≠ GEKSJt,t-d.
For the CLIP, there are two reasons. The first reason is that the clusters are weighted together arithmetically, so that:
The second reason is that the clusters that would be formed if the current period was used as a base for the clustering may be different to those formed when clustering on the base period. This is not a fault of clustering, as consumers would have chosen different products given what was available on the market at that point. Overall, if the clusters were geometrically aggregated then the CLIP would pass this axiom given that the clusters are equivalent in the base and current period.
There are two potential reasons why the FEWS fails this test; either the fixed effect regressions provide different answers when running the regressions reversing time, or the splicing factors are different.
Simulations can be run to test which factor is more important. First, an artificial dataset is generated, simulated from the following formulae:
pit = pi0 + βi t
where the initial prices are a set of random numbers drawn from the gamma distribution with shape parameter 20 and rate parameter 2:
pi0 ∼ Γ (20,2)
and the gradient is drawn from a standard uniform distribution, that is:
βi ∼ U [0,1].
Figure 5: Fixed Effects with a Window Splice (FEWS) index from simulated data
Source: Office for National Statistics
Download this chart Figure 5: Fixed Effects with a Window Splice (FEWS) index from simulated data
Image .csv .xlsAn Index calculated from this data can be seen in figure 5. From this data, P0,1000 =43.06169 and the reciprocal of P1000,0 is 43.06169. On this level of precision, the axiom appears to hold, however when the difference between the two indices are taken the difference is equal to 1.588987×10-10. The FEWS can be decomposed as the product of the Fixed Effects index and the splicing factors. For P0,1000 this decomposition is 1.011574 for the Fixed Effects index and 42.5698 for the splicing factors. For the reciprocal of P1000,0, the Fixed Effects index is 1.634896 and the splicing factors is 26.339094. This difference in decomposition is the reason that the indices are different. The main contributors to this difference are the fixed effect index factors, which might be because the indices are calculated on different estimation windows.
Axiom 9 [Circularity Test]
P ( p0 , ps ) P ( ps , pt ) P ( pt , p0 ) = 1
If an index is calculated from period 0 to an intermediate period s, from s to t, from t back to 0 and then chained, the resulting index should not show any change.
All indices that fail the Time Reversal Test fail the Circularity Test due to the reversal of the time periods in the final chain.
Axiom 10 [Monotonicity in Current Prices Test]
P ( p0 , pt ) < P ( p0 , p ) if pt < p
Axiom 11 [Monotonicity in Base Prices Test]
P ( p0 , pt ) > P ( p , pt ) if p0 > p
All indices pass these axioms as all the functions are monotonic. This can be shown as follows.
Proof
Let p > pt (in other words pi > pit ∀ i), then for all indices that are based on price relatives the following is obtained:
pi > pit ∀i
divide by the base price for each product
taking the geometric mean of both sides
Since the geometric mean of the price relatives using the current prices ( pt ) is less than using the larger prices ( p ) this means that P ( p0 , pt ) < P ( p0 , p ). For price indices that use the ratio of averages the proof is the same (that is, taking the average of the prices then dividing by the average base price).
For Monotonicity in base prices you get the following:
pi > pi0 ∀i
divide into the current price for each product
taking the geometric mean of both sides
Since the geometric mean of the price relatives using the base prices is greater than using the larger prices this means that P ( p , pt ) < P ( p0 , pt ). For price indices that use the ratio of averages the proof is the same (that is, taking the average of the prices then dividing by the average base price). For the quality adjustments in the FEWS they would be the same for both p and pt as the increase in the price would be absorbed into the time dummy coefficients.
Axiom 12 [Price Bounce Test]
The price index should not change if prices are rearranged and then returned to their original order:
All indices except the Fixed Based Jevons fail the Price Bounce Test in the presence of product churn. This is due to the unmatched products that have to be removed from the calculations.
Example 4.1
Table 1 contains a set of prices for three different products where the prices are bouncing. After the third period, products start churning.
Table 1: Example prices for three products
| Product\Time | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| A | 1 | 3 | 1 | 3 | 1 | 1 | |
| B | 2 | 1 | 2 | 1 | 2 | 1 | 2 |
| C | 3 | 2 | 3 | 3 | 2 | ||
| Source: Office for National Statistics | |||||||
Download this table Table 1: Example prices for three products
.xls (26.1 kB)Table 2 contains the corresponding price relatives for these prices (taking the previous period as the base period). Please note that it is slightly sparser than Table 1 because of the compounding factor of the missing prices.
Table 2: Example price relatives for three products
| Product\Time | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| A | 1 | 3 | 0.33 | 3 | 0.33 | ||
| B | 1 | 0.5 | 2 | 0.5 | 2 | 0.5 | 2 |
| C | 1 | 0.66 | 1.5 | 0.66 | |||
| Source: Office for National Statistics | |||||||
Download this table Table 2: Example price relatives for three products
.xls (18.4 kB)A Chained Bilateral Jevons index can be calculated from these price relatives in Table 2. When the products are not churning, you can see that the Chained Bilateral Jevons is not affected by price bounce. However, when the product goes out of stock, the Chained Bilateral index is affected by price bounce. The same happens for the GEKS-J index but the calculations are more complicated.
Table 3: Bilateral Jevons indices PJt-1,t and Chained Bilateral Jevons indices PCBJ0,t for the three products
| Time | PJt-1,t | PCBJ0,t |
| 0 | 1 | 1 |
| 1 | 1 | 1 |
| 2 | 1 | 1 |
| 3 | 1.22 | 1.22 |
| 4 | 0.82 | 1 |
| 5 | 0.58 | 0.58 |
| 6 | 2 | 1.16 |
| Source: Office for National Statistics | ||
Download this table Table 3: Bilateral Jevons indices P~J~^t-1,t^ and Chained Bilateral Jevons indices P~CBJ~^0,t^ for the three products
.xls (26.1 kB)4.1 Summary of axiomatic approach
Table 4 shows whether the indices under consideration passed or failed each of the axioms considered.
Table 4: Summary of index performance under the axiomatic approach
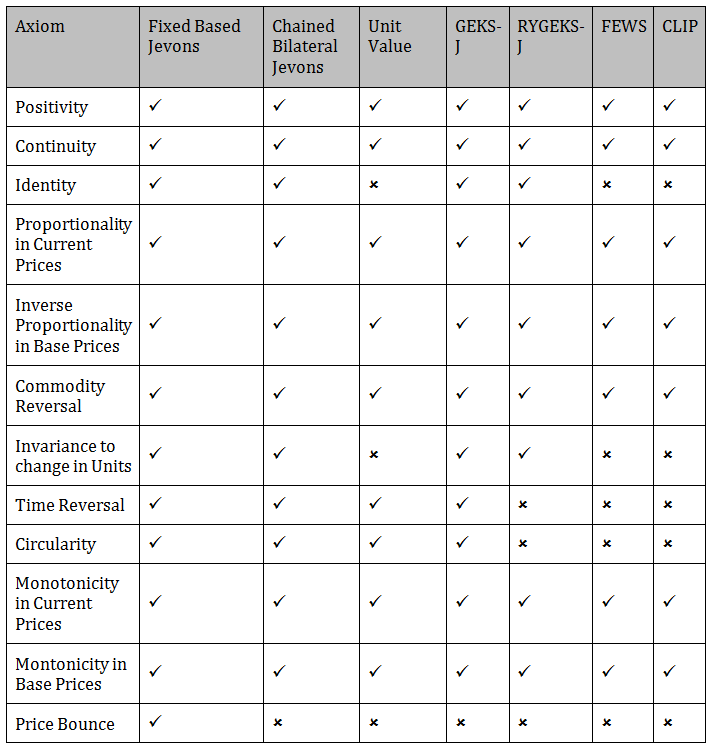
Source: Office for National Statistics
Download this image Table 4: Summary of index performance under the axiomatic approach
.png (33.5 kB)In summary, only the Fixed Based Jevons index passes all of the axioms. However, this is not suitable for a monthly production index because it relies on products existing in every month. Figure 6 uses ONS web scraped data for strawberries to demonstrate how the Fixed Based Jevons fails when products are not consistently in the dataset each month.
Figure 6: Comparison of indices based on web scraped data for strawberries, Index June 2014 =100
UK, June 2014 to March 2017
Source: Office for National Statistics
Download this chart Figure 6: Comparison of indices based on web scraped data for strawberries, Index June 2014 =100
Image .csv .xlsFor 2016, there is no product that exists in every month, in particular, from September onwards there are no products on the market that were sold in the first 8 months of the year. Therefore, a Fixed Basket Jevons index cannot be calculated as the set of matching products is empty, that is, ( S * =∅.
The GEKS-J and the Chained Bilateral Jevons index pass all axioms other than price bounce. Therefore, under the axiomatic approach, the GEKS-J index and the Chained Bilateral Jevons index also perform well. According to Ivancic, L. [2011] the GEKS methodology eliminates chain drift. Therefore, if a method that does not suffer from chain drift is desired then the GEKS-J method is recommended.
Notes for: The test/axiomatic approach
- This is one of the tests that may be deemed less relevant as two commonly used price indices, the Laspeyres index and the Paasche index, fail this test as well.
5. The economic approach
The economic approach to index numbers assumes that prices and quantities are interdependent. This means that the quantity of a product bought depends on its prices; q = q ( p ), that is, the quantities are functions of prices. This allows the consumer to adjust their spending depending on how relatively cheap or expensive the product becomes. In the context of consumer prices, the economic approach usually requires the chosen index formulae to be some kind of Cost of Living index (COLI).
This approach considers the indices against the COLI. However, it is important to note that this is not appropriate in the context of choosing a methodology that is suitable for use in the Consumer Prices Index including owner occupiers’ housing costs (CPIH).
This is because the CPIH measures the change in prices of goods and services purchased to be consumed; this is different to a COLI, which measures the change in the cost of obtaining a certain level of utility given the different prices. In the CPIH, the consumption (that is, demand) is fixed, whereas a COLI allows for demand to change as prices change. Therefore, even if an index approximates or is exact for a COLI, it might not be a good index to use in the context of the CPIH. However, the results of assessing each index against the economic approach are presented here to provide useful reference to other national statistical institutes (NSIs) who produce a COLI alongside their other consumer price statistics.
The economic approach is based on consumer preferences. A consumer chooses the combination of products that they most prefer out of all that they can afford. It is easy to define what is meant by “afford” by defining the budget set (Definition 5.1).
Definition 5.1 [Budget set]
For a set of products q with prices p and total budget x, then the budget set B is defined as:
A budget is exhausted when
A consumer can afford a combination of products if that combination is within the budget set. Defining preferences is slightly less easy to do, but this is managed through the utility function. A utility function can only be used when the consumer’s preferences are "well-behaved"1. The utility function assigns a number to a set of products and preserves preferences, for example, if the consumer prefers a set of good X to a set of good Y, that is, X≺Y, then u(X) < u(Y) where u is the utility function.
A utility function allows us to summarise a large amount of data in a few values. In this context, the actual values of the utility function are not significant; we are just focusing on the ordering of preferences.
To see this, let u1 and u2 be two utility functions and X and Y be two consumption bundles such that u1(X)=5, u1(Y)=10, u2(X)=20 and u2(Y)=25. Both utility functions show that X≺Y so the actual utility functions chosen don’t matter. However, it still allows us to identify sets of goods, which consumers are indifferent to (Definition 5.2).
Definition 5.2 [Indifference]
For two sets of goods X and Y, a consumer is indifferent between them if u(X)=u(Y). This is shown as X∼Y
Figure 7 presents some example indifference curves, which correspond to the utility function u ( q ) = 2ln ( q1 ) + 2ln ( q2 ). The indifference curve labelled u = 12 gives all combinations of good one (X) and good two (Y), which give the consumer a utility of 12.
Figure 7: A utility function with three indifference curves labelled
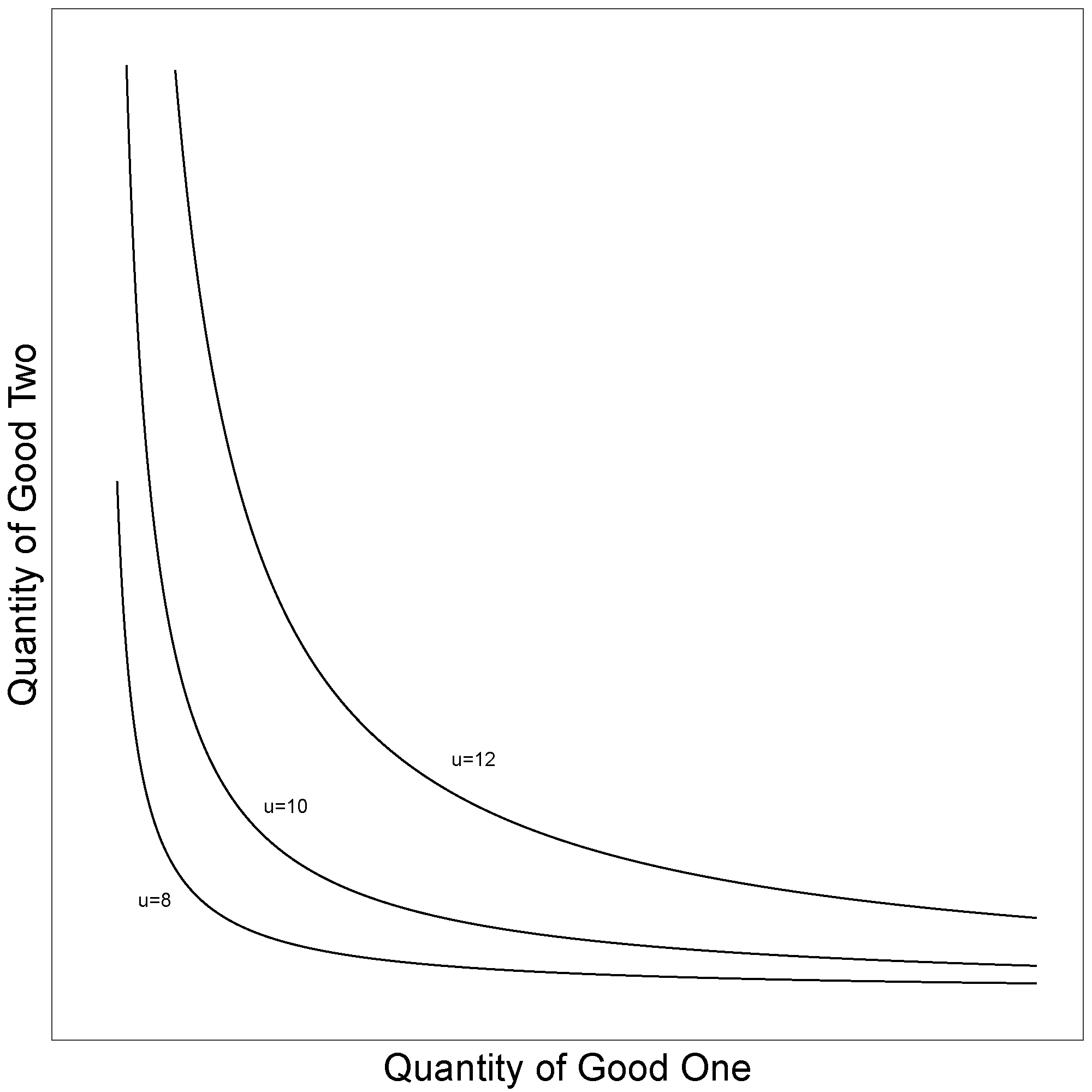
Source: Office for National Statistics
Download this image Figure 7: A utility function with three indifference curves labelled
.png (20.5 kB)What economists mean by "prefer" and "afford" in the following statement: "A consumer chooses the combination of products which they most prefer out of all they can afford" can be rewritten as: "Consumers get on to the highest indifference curves, subject to their budget constraint".
This is shown in Figure 8. The consumer’s budget constraint, q1 + 594 q2 = 594, is the straight line and their budget set B is the shaded triangle. In this example, two utility curves fall within the budget set: one where the utility is equal to 8 and the other when the utility is equal to 10. The consumer can therefore buy any set of products on the u = 8 line and the u = 10 line. As the consumer is assumed to want to maximise their utility they will buy the set of goods where the budget line touches their highest indifference curve ( u = 10 ). Buying this set of products also exhausts their budget.
Figure 8: A utility function with a budget constraint
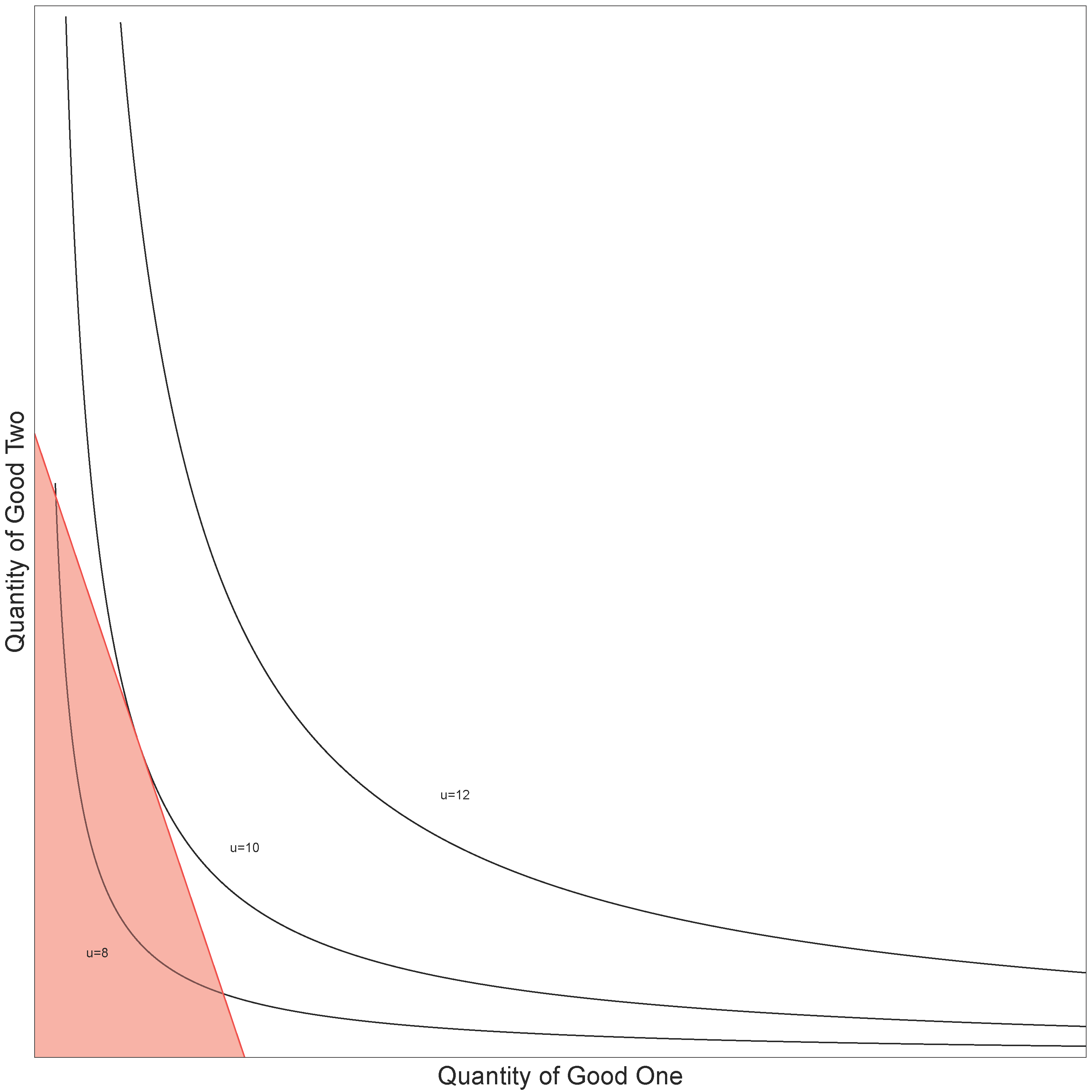
Source: Office for National Statistics
Download this image Figure 8: A utility function with a budget constraint
.png (64.6 kB)Mathematically, this process of the consumer choosing their most preferred set of products out of those that they can afford is a constrained maximisation problem, which can be defined as:
Solving this constrained maximisation gives us the result that quantities depend on prices because the solutions are of the form:
that is, the quantities bought are a function of the prices observed and the consumer budget. This solution is called the indirect utility function, v(p,x) and gives the maximum utility that the consumer can reach given the prices faced and the available budget.
For the example utility function (u( q ) = 2ln ( q1 ) + 2ln ( q2 )), the quantities that maximise it given the budget constraint are
and
In this situation, the quantities are dependent on the price (if the price of a good doubles then the quantity bought halves).
The indirect utility function can then be derived as:
The inverse of the indirect utility function is called the cost function, c ( p , u ), and represents the minimum cost of reaching a given level of utility, given the prices that the consumer faces. The cost function essentially says that if a consumer is given a choice of different sets of products to which they are indifferent, then the consumer will choose the least expensive. For this indirect utility function, the cost function is:
This means that when the prices are p0 then the consumer will choose to buy q0 of the products. If prices change to p1, then the consumer may not want to buy q0 (the quanity that is assumed in the fixed basket approach, such as the Fixed Based Jevons). Instead, they might change to another combination of products q* where u ( q0 ) = u ( q* ). This allows for the substitution of products that have become relatively expensive towards those products whose relative price has fallen.
A Cost of Living index (COLI) allows for this behaviour to be taken into account in the calculation of the index (Definition 5.3).
Definition 5.3 [Cost Of Living index]
A Cost of Living index PK is the ratio of the cost of achieving a given utility at current period prices to the cost of achieving a given utility at the base period prices:
Figure 9: Demonstrating a Cost of Living index
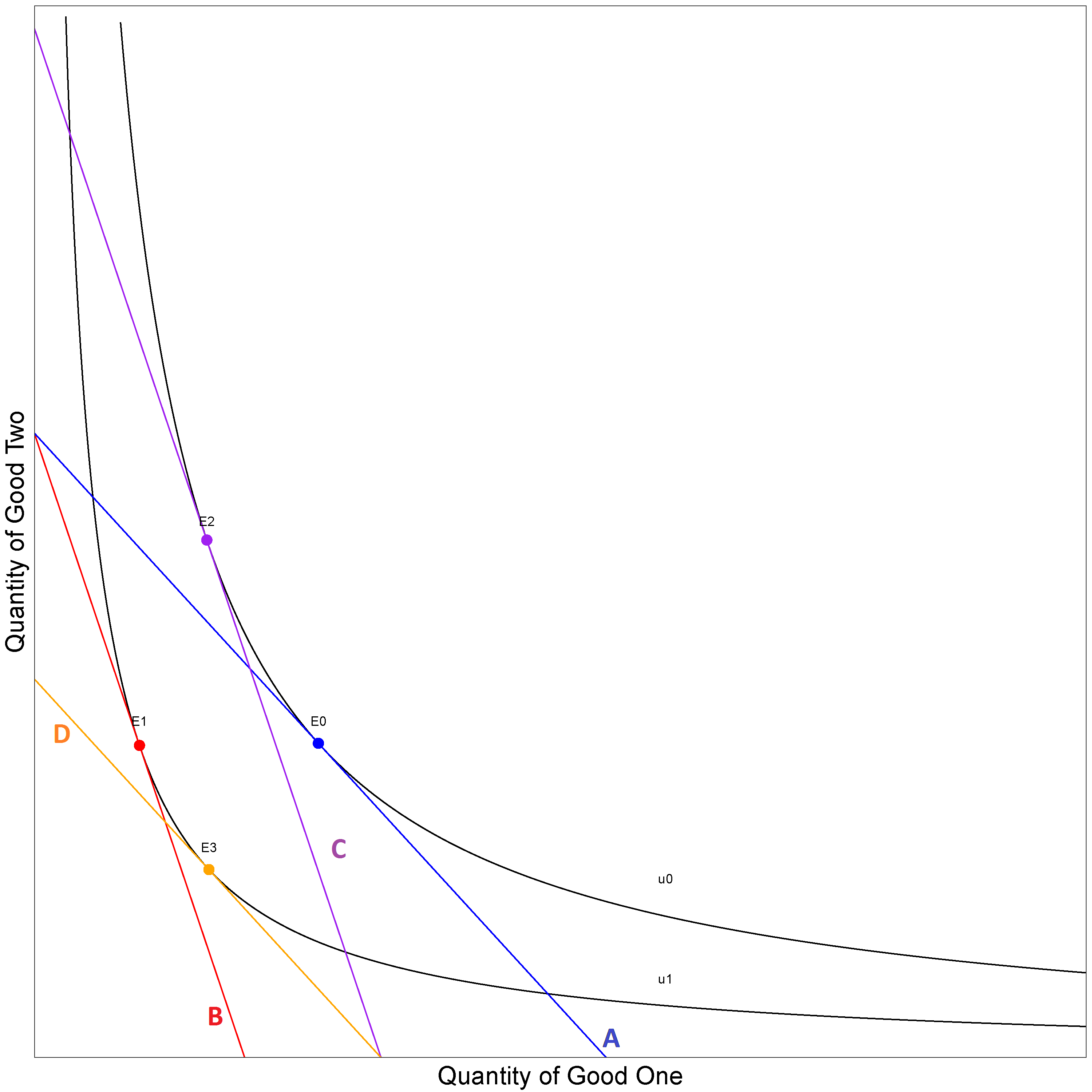
Source: Office for National Statistics
Download this image Figure 9: Demonstrating a Cost of Living index
.png (90.9 kB)Figure 9 illustrates a COLI. At period 0 prices the budget constraint is line A and the highest indifference curve that can be obtained with that constraint is u0 at the point E0. E0 is the cost of attaining utility u0 at base prices. When the price of good one increases in the next period, the budget set moves down to line B. This means that the original indifference curve can't be reached. Instead a new indifference curve is reached, which meets u1 at the point E1. E1 is the cost of attaining the utility u1 at current prices.
A COLI index can either use the cost of attaining the utility u0 at current prices or the cost of attaining the utility u1 at base prices. This can be achieved by moving the respective budget constraint to become tangential to the desired utility function. This is what the lines C and D represent in Figure 9.
Line C is the budget constraint at period 1 prices shifted to attain the original utility. The distance that it has been shifted is called the compensated variation; the amount that the consumer’s income needs to be increased in order to offset inflation. From this, it can be seen that the cost of achieving the original utility is the point E2, which is different to the cost at base prices, E0, in this example. As prices changed, the consumer then substituted from the quantities consumed at E0 to the quantities consumed at E2.
In contrast, if utility u1 is used instead, the budget constraint at base prices, line A, is shifted down and becomes line D. The distance by which it is shifted is called the equivalent variation; the amount of consumer’s income that needs to be taken away at the base price level, to have the same impact on their utility as inflation between the two periods. Another cost is calculated, the point E3, which is the cost of attaining the current utility at base prices. Therefore, if the consumer faced period 0 prices on this utility curve they would substitute to E3.
In summary, there are two cost of living indices, one for each utility level. In general, PK ( p0 , p1 , u0 ) ≠ PK ( p0 , p1 , u1 ), which means that a COLI depends on the level of utility.
However, if the cost function can be written as c ( p, u ) = a (p) b ( u ) (which comes about if the utility function is homothetic), then the COLI doesn't depend on the level of utility. Using the example given, the cost function is already written in the form c ( p , u ) = a ( p ) b ( u ) where a ( p ) = √( p1 p2 ) and
This means that the COLI is:
This utility function was chosen because the consumer preferences that it represents mean that the COLI can be written as being equal to a Fixed Based Jevons and a Unit Value. This demonstrates how the economic approach can be used as a way of evaluating the indices; the aim is to identify a particular set of preferences that mean that the indices can be classified into one of three groups:
- approximate
- exact
- superlative
An index approximates a COLI if it appears in a Taylor expansion of the COLI index (for example, Paasche and Laspeyres indices are approximate). An index is exact for a COLI if under a certain form of consumer preferences the resulting COLI index is equal to a known index formula. A superlative index is an index that is exact with a cost function that has a flexible functional form2. The Törnqvist and Fisher are both exact and superlative indices. For this work, the exact class of indices is going to be used.
There are two caveats to using this consumer preference theory: the consumer is assumed to be rational, and the consumer aims to maximise their utility when making their choice. There have been many experiments to test these assumptions, for example Harbaugh et al. [2001] tested this on children aged 7 and 11, and on economics undergraduates. They found that 26%, 62%, and 65% respectively were "rationalisable". Beatty and Crawford [2011] looked at the Spanish Continuous Family Expenditure Survey from 1985 to 1997 and found that 95.7% of those in the survey were consistent with the theory.
There are many different types of preferences that economists have developed to explain consumer behaviour, two of which are useful for this work: Cobb-Douglas preferences and Stone-Geary preferences.
Definition 5.4 [Cobb-Douglas preferences]
A consumer has Cobb-Douglas preferences if their preferences can be explained by the following utility function:
which has the following cost function:
Definition 5.5 [Stone-Geary preferences]
A consumer has Stone-Geary preferences if their preference can be explained by the following utility function:
which has the following cost function:
From Cobb-Douglas preferences the following result is found:
where wj = m ( wj0, wjt ) with m a function such that m (x,x) = x. The arithmetic mean is a function that has this property. This means that any geometric index is exact under Cobb-Douglas preferences. Since the indices under consideration involve a geometric mean, they may be exact indices.
Let’s take the Jevons index:
This is equivalent to the geometric index formulae if the weights are set equal to 1/n. This means that the Jevons index is an exact index under Cobb-Douglas preferences.
The Unit Value index doesn't look like the form that is required for the geometric index, although it can be rewritten to show that it fits in this form:
The weights are defined as:
In this solution, the first case is when a product disappears, and the last is when a product is introduced. Using this, the Unit Value index is also exact for Cobb-Douglas preferences. This might show a downside to the economic approach in that a type of preference does not give a unique solution.
Further research is required to find a set of preferences for which an arithmetically aggregated CLIP is exact or if it approximates a COLI. However, a geometrically aggregated CLIP mentioned in the axiomatic approach would be exact. This can be shown by augmenting the unit value weights to incorporate the clusters. The extra case is required in the event that a product moves between clusters in the different time periods:
Neary and Gleeson [1997] show that Stone-Geary preferences lead to a GEKS index, and therefore a GEKS index is exact. Balk [2001] also looks to find preferences for GEKS, in the context of international comparisons. Using a Stone-Geary preference structure for the GEKS makes sense in that the demand function depends on all prices whereas the demand function for Cobb-Douglas only depends on the price of the product in question.
The Fixed Effects index with a Window Splice (FEWS) index, more specifically the fixed effects part of the index, is a hedonic index. It adjusts the index to account for the change in quality of the new set of products in the index. The hedonic indices also come from economic theory and can be placed in the utility maximisation, consumer theory paradigm. The dual problem to the utility maximisation is the following minimisation:
In the hedonic space, the quantities of the goods aren’t important; rather it is the characteristics that the goods have that affect the regression. Therefore, the minimisation problem changes to be over the characteristics, that is, the minimisation then becomes in the hedonic space:
where h is the hedonic function and Uh is the utility function in the hedonic space. This can then be used to calculate COLIs depending on the choice of hedonic function. In this case the hedonic function is the time product dummy. For more information please see Triplett [2006] about hedonics and Diewert [2003] on hedonics in relation to consumer theory.
In summary the economic approach gives little insight into which formulae to use because the indices are all exact under a certain set of preferences, and therefore no clear conclusions can be drawn.
Notes for: The economic approach
- “Well-behaved preferences” mean that they are complete, reflexive, transitive, monotonic, convex and continuous, and there exists a continuous function that describes those preferences, (Debreu [1964]).
- A flexible functional form f is a functional form that has enough parameters in it so that f can approximate an arbitrary, twice continuously differentiable function f* to the second order at x*. Thus f must have enough free parameters to satisfy the following 1+N+N(N+1)/2 equations. f ( x* ) = f* ( x* ); ∇ f ( x* ) = ∇ f* ( x* ) ; ∇2 f ( x* ) = ∇2 f* ( x* );
6. The statistical approach
The statistical approach to index number theory treats each price relative as an estimate of a common price change. Hence, the expected value of the common price change can be derived by the appropriate averaging of a random sample of price relatives drawn from a defined universe. These are effectively models for inflation rates.
For example, the most simplistic model of price change is the following model:
Here π is the common inflation rate and εi is the error for product i. This essentially assumes that price changes are normally distributed. The Ordinary Least Square (OLS) estimator or maximum likelihood estimator (MLE) for this model is the Carli index:
If instead it is assumed that price changes are log-normally distributed, then the model that prices follow is:
where θ=logπ is the log inflation rate. The OLS and MLE estimates of θ is:
and therefore the estimate of π is:
which is the Jevons price index.
These examples show that different models will give different inflation rate estimates. These estimators can also be derived from a design-based survey sampling methodology.
As well as this form of price change (that is, a constant term π plus an error term εi), there are different forms that can be used. A second set are models of the form:
Models of this form are known as ratio estimators.
The Dutot index can be directly derived from the above, as:
If log prices are used in the place of prices, a ratio estimator of the log inflation rate is obtained:
This gives a Jevons index in the case of a matched sample, (Silver and Heravi [2006]). In the case of unmatched samples, which are more likely to be the case given the use of web scraped data, a Unit Value index can be derived. This shows that the Unit Value index is a geometric equivalent of the Dutot index.
The Unit Value index is sensitive to heterogeneity in the products, as is the Dutot index. Silver and Heravi [2006] suggest hedonically adjusting to control for this heterogeneity, but this is difficult without characteristic information. However, the way that the CLIP is designed should overcome this heterogeneity. This is because the CLIP stratifies a Unit Value index by defining the strata as the local maxima of the kernel density estimates, using a clustering algorithm. These strata should then be homogeneous. This stratification improves the precision of the estimate, as elements within strata would have similar values, and between strata should have different values, (Lohr [1999]).
As an example, Figure 10 shows the price distributions of tea bag prices for Office for National Statistics (ONS) web scraped data and the published Consumer Prices Index including owner occupiers’ housing costs (CPIH) microdata. Both modes of collection show that there is some heterogeneity in the prices, and therefore a unit value would be sensitive to this. The CLIP methodology should help to overcome this. In the CPIH, the heterogeneity may also be reduced by the current stratification in the compilation of the index; for example, tea is stratified by region and shop type.
Figure 10: The distribution of tea bag prices in the published CPIH micro-data (blue) and the ONS web scraped data (pink), January 2015
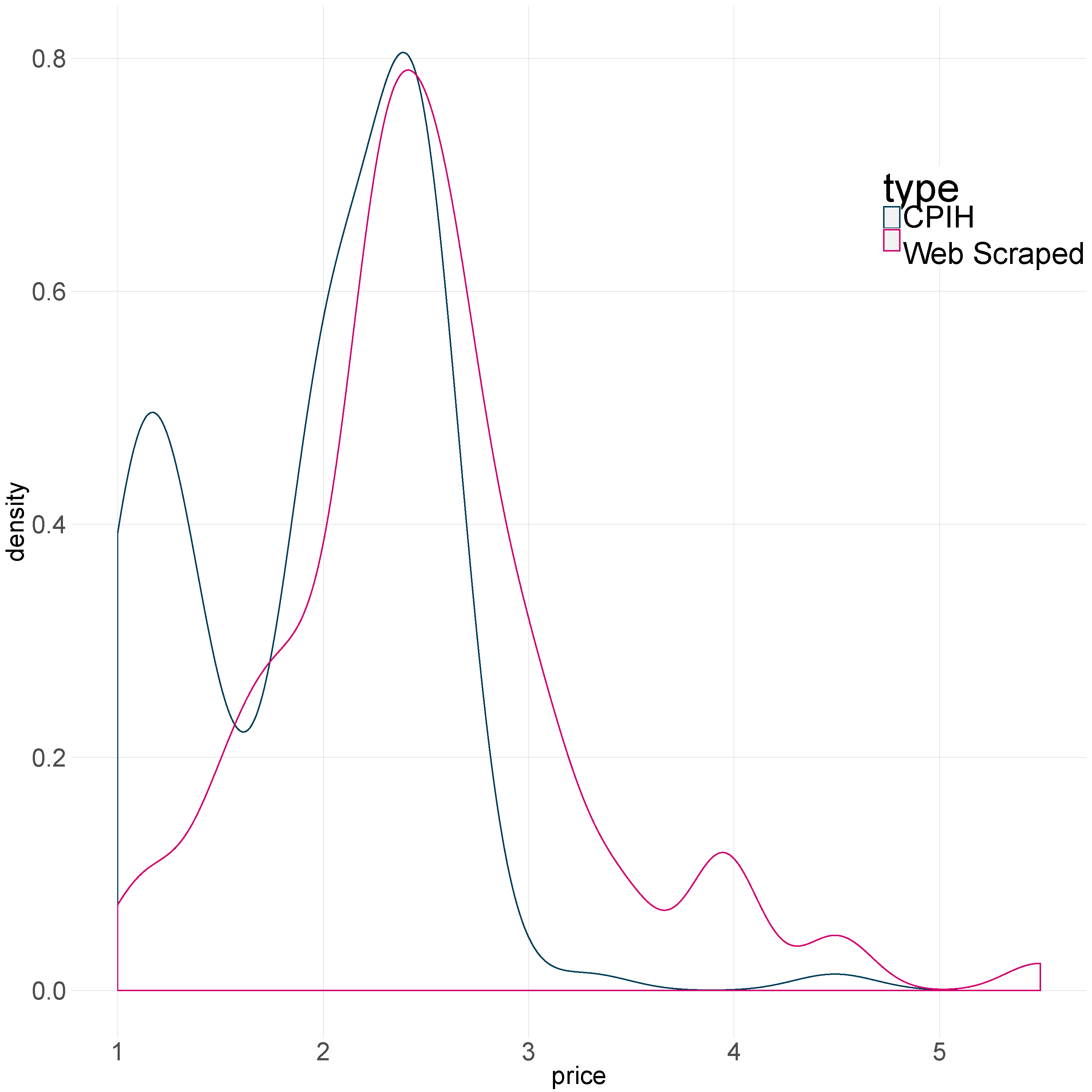
Source: Office for National Statistics
Download this image Figure 10: The distribution of tea bag prices in the published CPIH micro-data (blue) and the ONS web scraped data (pink), January 2015
.png (67.7 kB)The weights, wh, used to aggregate the CLIP can be interpreted as the probability of a product being in that cluster or strata in the base period. These weights can be used to aggregate the estimates of the inflation rate or to aggregate the estimates of the log inflation rates give two different versions of the CLIP. If the weights are applied after estimating πh, (that is, the stratum-specific inflation rates using prices), the Arithmetic CLIP (ACLIP) is obtained. If the weights are applied after estimating θh (that is, the stratum-specific inflation rates using log prices) then the Geometric CLIP (GCLIP) is obtained:
The next set of models combine the two previous forms. That is, the variables that are used in the model are price relatives, but the estimators are ratio estimators. Let’s suppose that the model is:
where j∈[0, t ] are the intermediate periods, and εij is the error for product i when going through intermediate period j. This gives us a ratio estimator, which equates to the Chained Jevons part of the GEKS-J index. If a 1/t weight is then given to each intermediate estimate of the log inflations, this gives a GEKS-J index, as follows:
The final set of models decompose price into constituent parts. These are what hedonic indices do. There are three types of hedonic models:
Linear characteristics:
where αj is the intercept at time j, βkj is the effect characteristic k has on the price at time j, and zik is the value of characteristic k for product i. The linear characteristics model assumes that the characteristic effects change over time.
The time dummy hedonic method:
This method assumes that the characteristic effects don't change over time, and includes a dummy variable, Dij, for which period the product was collected:
where δt is the time-specific effect.
The time product dummy method:
This method can be used when detailed characteristic information is not available, and a dummy variable, Di, for the product is created:
where γi is the product-specific effect and the Nth product is taken as the reference product. This method assumes that the quality of each distinct product is different to the quality of other products to a consumer. It is a reasonable assumption as the number of potential characteristics is large and not all of them are observable. The time product dummy is also equivalent to a fully interacted time dummy method.
The method that was used in this work was the time product dummy (TPD) method. A TPD index is the same as a Fixed Effect index (FE), which is the basis of the FEWS.
Now that all of the indices have a statistical model associated with them, the statistical approach becomes a model-fitting exercise. This involves selecting the model which “best fits'' the data. In this context, best fit means that the model is chosen that minimises the information lost from using this model to fit the data. The Akaike Information Criterion (AIC), (Akaike [1974]), was used to measure this fit. The AIC is defined as:
where k is the number of parameters in the model, L is the likelihood function for that model, and which is evaluated at the maximum likelihood estimator (MLE) of the parameter θ.
The models for the Jevons, Unit Value, GEKS-J and FE/TPD were fitted to a sample of items from the grocery collection, clothing data and the “central collections”1 project. For the grocery and clothing data, daily prices were used to fit the models. Two months of data were used; one being from a period when the CPIH 12-month growth rate was around 1% (June 2014) and the second from a period when the CPIH 12-month growth rate was around 0% (June 2015). This was done to test whether different inflationary environments caused a change in “best" model. The centrally collected items are collected monthly and the whole time series was used.
Table 5 presents a summary of index performance under the statistical approach. It is worth noting that for the groceries and the clothing data, the FE/TPD overfits the data. This overfitting is due to the large number of product dummy parameters in the estimation, and confirms the problems with the TPD index that De Haan et al. [2016] present in their research.
Table 5: Summary of index performance under the statistical approach
| Group | Best Fit |
| Groceries | Fixed Based Jevons |
| Clothing | Unit Value |
| Central Collection – Chart | Fixed Based Jevons |
| Central Collection – Technological | Fixed Effects |
| Source: Office for National Statistics | |
Download this table Table 5: Summary of index performance under the statistical approach
.xls (26.1 kB)From the statistical approach, the Unit Value index was identified as the preferred index to use on clothing items. Stratification improves the precision of the estimate if the sampling units are homogeneous within a stratum and heterogeneous between strata. As the CLIP is a stratified Unit Value index, it follows that it should be a better approach to use for this category.
Assessing the indices against the statistical approach provides evidence to suggest that no single index is suitable to cover the full range of items in the CPIH basket of goods and services that could be sourced from web scraped data.
Notes for: The statistical approach
- Prices for these centrally collected items are obtained manually by ONS price collectors through websites, phone calls, emails, CDs and brochures. Centrally collected items cover approximately 26% of the CPIH basket. As part of its research into alternative data sources, ONS is currently piloting alternative ways of collecting these data through “point and click" web scraping software.
7. Summary and recommendations
The axiomatic and statistical approaches to index number theory identify different indices as being more appropriate for particular categories of items. This section considers from a methodological viewpoint how these indices could be incorporated in the Consumer Prices Index including owner occupiers’ housing costs (CPIH). The economic approach was not considered here because even if an index approximates or is exact for a Cost of Living Index (COLI), it might not be appropriate in the context of the CPIH (Section 5).
7.1 Grocery prices
When considering both the axiomatic and statistical approaches, the GEKS-J is the most appropriate index to use for groceries within the CPIH basket. This is due to its axiomatic properties and because the GEKS-J is designed to limit chain drift, (de Haan and van der Grient [2006]).
The statistical approach also suggested that for groceries a Fixed Based Jevons index may also be appropriate. It is common practice to periodically chain indices to allow for new products entering the market. While the Chained Bilateral Jevons does chain the indices to allow for new products entering the market, the presence of product churn results in the index displaying chain drift.
In the construction of the GEKS-J, the Bilateral Jevons between base and intermediate period is chained with the bilateral Jevons between the intermediate and current period. This reduces any chain drift that would have occurred when calculating a Chained Bilateral Jevons between the base and current period. However, chain drift is also observed when the GEKS-J index is chained, a full proof of which is provided in Appendix A:
The Australian Bureau of Statistics has also used the GEKS index with a Törnqvist (GEKS-T) base in their CPI (Kalisch [2016]), with a mean splice as an extension method (Kalisch [2017]). Extension methods extend the index beyond the initial observation window, with a choice of which period to chain the index onto. There are a number of extension methods that can be used:
- the window splice is where the index is spliced in the start of the window
- the half splice is where the index is spliced in the middle of the window
- the movement splice is where the index is spliced at the end of the window
- the mean splice is where every period is used as a splicing period and the geometric mean of the periods is used as the splicing factor; for a detailed description of the method see Kalisch [2017].
These extension methods help to overcome the traditional problem associated with formulating a GEKS index, which is that it is open to revisions. This is because it involves using price movements from the current period to future periods, which is overcome if these splicing methods are used. These extension methods also reduce the loss of characterisiticity when using multilateral methods on long time series.
Office for National Statistics (ONS) developed another solution to this problem: an ”In Period GEKS-J", where only data observed up to the current period are used in the calculation of the index. This means that when a new period's data is collected, the new data is only used to calculate the current period index, and is not used to recalculate the historical series. The “In Period GEKS-J” has been used throughout this review.
Another potential problem with the GEKS index is that it is responsive to atypical prices. Chessa et al. [2017] demonstrates that the GEKS-T is sensitive to these prices, mainly those associated with products that have been “reduced to clear”, referred to by Chessa as “dump prices”. Rewriting equations 13 to 15 of Chessa et al. [2017] in the notation introduced earlier, the second part of the GEKS, from the intermediate period to the current period is:
where:
The denominators are adjustment factors, with the second denominator akin to quality adjustment. The vj' cause the problem with dump prices, as these are average prices over the period and therefore will be smaller. This means that the products with dump prices will have higher weights. When this decomposition is used in the GEKS-T formula this becomes more apparent:
Only these average price adjustments remain. Therefore the index has a downward bias as these values decrease when the dump prices are assigned higher weights, and the difference in expenditures shares is greater than 0 for existing products. This bias is shown in the Dutch scanner data, which is the reason that Chessa et al. [2017] discourages the use of the GEKS-T.
However, products showing dump prices would not be used in the compilation of indices from web scraped data. Firstly they would be flagged as anomalous through the cleaning procedure used on the web scraped data, (Mayhew and Clews [2016]), and the Tukey algorithm used in the CPIH production process (Chapter 6, ONS [2014a]). Secondly, these dump prices are associated with end of line products, which are not collected in the CPIH as they are deemed not to be of the same quality as, or comparable with, goods previously priced, or those likely to be available in future (Chapter 8, ONS [2014a]).
7.2 Clothing prices
When considering the axiomatic and statistical approaches, the Clustering Large datasets into Price Indices (CLIP) index is considered the most appropriate index to use for clothing within the CPIH basket due to several factors. From the statistical approach, the Unit Value came out as the index that best fitted the data. However, due to the heterogeneity in clothing prices the CLIP will be more appropriate due to the use of clustering, which creates homogenous strata resulting in a more precise estimator.
Secondly, work conducted by Payne [2017] and ONS [2017] shows that Fixed Effects index with a Window Splice (FEWS) and variants of the GEKS-J gave implausible estimates of clothing inflation using web scraped clothing data. This is shown in Figure 11 for men's jeans and Figure 12 for women's coats.
Figure 11: Comparison of indices based on web scraped data for men’s jeans
UK, August 2014 to October 2015
Source: Office for National Statistics, WGSN
Download this chart Figure 11: Comparison of indices based on web scraped data for men’s jeans
Image .csv .xlsFigure 12: Comparison of indices based on web scraped data for women’s coats
UK, September 2013 to October 2015
Source: Office for National Statistics, WGSN
Download this chart Figure 12: Comparison of indices based on web scraped data for women’s coats
Image .csv .xlsFigures 11 and 12 illustrate that, over the periods covered, the FEWS and RYGEKS indices show prices decreased by 20 and 35 percentage points respectively for men's jeans and 55 and 80 percentage points respectively for women's coats. In contrast, the CLIP illustrates that men's jeans have increased by 10 percentage points and women's coats have decreased by 20 percentage points. Movements in the RYGEKS-J are due mostly to the dump prices as discussed in Section 7.1, whereas the FEWS over-adjusts for quality change when introducing new products, a factor shown when the time product dummy (TPD) was overfitting for clothing prices.
Clustering also has its advantages in the price collection itself. Clothing prices have been difficult to price in the CPIH collection due to seasonality, fashionabilty and sales of clothing. De Vincent-Humphreys [2017] demonstrates that by the end of a year 85% of the products priced in January have been replaced, with 25% of the clothing products within each month being replacements. The comparability of replacement items will have less of an effect on the CLIP than traditional Consumer Prices Index methodology because the clusters in the CLIP remain constant even when the mix of products changes.
7.3 Central collection - central items
The central collection is used for items where the prices can be collected centrally by ONS as national pricing policies are in place. As part of the web scraping project, there is a strand of work that aims to assess the feasibility of using point-and-click web scraping tools to facilitate the central collection of prices that currently takes place manually within the Prices division at ONS. The items used in the feasibility study can be broken down into three categories:
- chart-based collections
- technological goods
- package holidays
Only chart-based collections and technological goods are considered further as part of this review.
7.3.1 Chart-based collections
When considering the axiomatic and statistical approaches, the Fixed Base Jevons index is considered the most appropriate index to use for chart-based collections within the CPIH basket. For chart-based collections, the best sellers’ chart is used to ensure the items being collected are representative of the items that consumers are purchasing. The prices of products at specific chart positions are then compared over time (for example, a CD that is number 1 in the chart in the base month will be compared with a CD that is number 1 in the same chart in the current month). The statistical approach found that the index that fitted this data the best was the Fixed Based Jevons.
It is also worth noting that the Fixed Effects/Time Product Dummy (FE/TPD) index is the worst fitting of all of the indices. This is possibly due to the definition of a “product'' within these items. For example, a product is defined as the DVD at chart position j. The position of the product changes as new DVDs enter the market, so the DVD at chart position j between one month and the next may not always be comparable in terms of genre and age classification among other factors. Therefore, when the FE/TPD makes quality adjustments it estimates a fixed effect for the chart position but even though it is the same chart position the underlying product is different. So the effect of being in this position isn't fixed, it’s more likely to be random.
Data collected for DVDs in our pilot study shows that the genre and age classification change month to month, meaning that the characteristics of the item aren't comparable. This may explain the poor fit for the TPD index. However, this does not necessarily mean that this method of collection for chart-based items is flawed from a quality point of view, as for these items the length of the films are approximately the same at 2 hours.
7.3.2 Technological goods
When considering the axiomatic and statistical approaches, the Fixed Effects with a Window Splice (FEWS) index is considered the most appropriate index to use for technological goods within the CPIH basket, based on the items that were analysed.
The FEWS is also justified when considering the nature of quality change within these items, as technological goods have a high level of replacements due to technological advancements. For example, in January a price for model A is collected. In March, model A is discontinued and model B replaces it with a higher price. Model B has increased storage compared with model A and this is reflected in the price. In the CPIH this quality change is corrected for using hedonic adjustments, (Chapter 8 ONS [2014a] and Triplett [2006]). Since the fixed effects part of the FEWS is a time product dummy hedonic model it is also adjusting for this quality change. This is in line with international best practice, (Krsinich [2014] and Krsinich [2015]).
Back to table of contents8. Future work
Although we have identified these indices as performing best against these methodological approaches, there may be other practical issues that require alternative index methodology to be used in future.
For example, the use of multilateral indices may not be compliant with current Harmonised Index of Consumer Prices (HICP) regulations. This will need further consideration when looking at the impact of using web scraped data in the Consumer Prices Index (CPI), and therefore the Consumer Prices Index including owner occupiers’ housing costs (CPIH). Eurostat is currently in the process of drafting some practical guidance for processing supermarket scanner data, which includes a section of which index methodology may be appropriate when using this data. Although not exactly comparable to web scraped data, the guidance can provide some useful direction on European compliance issues.
Internal system development is another practical issue that should be taken into account, as currently the system is only built to calculate Jevons, Dutot, and Carli indices as its elementary aggregates, and only accepts one price quote per product each month. The system would have to be rebuilt to cope with the multilateral methods and the regressions.
Further research is also required on the impact that the lack of expenditure weights for web scraped data will have on the index. Expenditure information can be used to remove products that may not have been purchased by many consumers (and therefore should not be included within a representative basket of goods and services). Early research by Statistics Netherlands (Chessa and Griffioen [2016]) that compares web scraped and scanner data for the same retailer and products shows that using equally-weighted web scraped data could introduce some bias into the index, although this can be mitigated by using expenditure proxies such as the number of days that a product is available on the website.
The frequency and coverage of the data should also be investigated further. For example, web scraped data can be collected on a daily basis for a near-census of products from a retailer’s website. This is in contrast to the traditional collection that focuses on a representative sample of products for a given item, which is selected to best cover consumer expenditure for a given class of Classification of Individual Consumption According to Purpose (COICOP). Prices for these products are collected at most once a month.
Questions remain for the indices identified as part of this review, for example, how do they perform when they use monthly, weekly or daily prices; should a sample of the web scraped data be taken instead and would this better suit the use of bilateral methods?
Finally, this research has shown that different methods are suitable for different areas of the CPIH basket. This implies that if we wanted to extend our coverage of web scraped data to other areas of the basket, further research is necessary to understand which index methodology is suitable for this particular area. As a next step, this will focus on understanding the requirement for package holidays.
Back to table of contents9. Acknowledgements
The author would like to thank the contributions of Rob Bucknall, Andrea Lacey, Alex Milroy, and Duncan Elliot of Methodology, Chris Payne, Tanya Flower, Himanshi Bhardwaj and Helen Sands of Prices Division, and Alexis Fernquest of the Data Science Campus, at Office for National Statistics; Professor Ian Crawford and colleagues at the Department of Economics at Oxford University, Antonio G Chessa of Statistics Netherlands, Frances Krisinch and Alan Bentley at Statistics New Zealand, Michael Holt and Marcel Van Kints of the Australian Bureau of Statistics, as well as the attendees at the 15th meeting of the Ottawa Group 2017 and the members of the Advisory Panel on Consumer Prices (Technical).
Back to table of contents10. Appendix: Proofs of chain drift
This appendix contains the proofs of chain drift in the Chained Bilateral Jevons and the GEKS-J indices.
A.1 Chained Bilateral Jevons
Proposition A.1
The Chained Bilateral Jevons index does have chain drift if there exists product churn in the dataset.
Proof
Let f in Definition 3.3 be the Jevons index, then Λ is the Fixed Based Jevons index and Λ* is the Chained Bilateral Jevons.
If S0,1 = S1,2 = S* (that is, there is no product churn) then:
hence if there is no product churn then the Fixed Based Jevons and the Chained Bilateral Jevons are equal.
If S0,1 ≠ S1,2, n0,1 = n1,2 and S0,1 ∩ S1,2 = S* ≠ ∅, (that is, there is product churn but the amount of items that have disappeared are replaced with the same amount of new products, and not all products have disappeared), then:
Therefore if there is product churn that keeps the number of products on the market constant over time then there exists some chain drift.
If S0,1 ≠ S1,2, n0,1 ≠ n1,2 and S0,1 ∩ S1,2 = S* ≠ ∅ (that is, products are churning but the number of products going out of stock aren't being replaced by the same amount of new products), then:
Therefore, in this type of product churn there is chain drift.
Finally, if S0,1 ≠ S1,2 and S0,1 ∩ S1,2 = ∅ (that is, all products are replaced) then:
This means that as none of the prices cancel out therefore in this type of product churn there is chain drift.
A.2 Chain drift in GEKS-J
Proposition A.2
The GEKS-J index does have chain drift.
Proof
Let f in Definition 3.3 be the GEKS-J index, then Λ (0,14) = PGEKSJ0,14 and Λ* (0,14) = PGEKSJ0,7 PGEKSJ7,14. The periods 0, 7 and 14 were chosen so that the multilateral nature of the GEKS-J can occur. If there is no chain drift then the ratio of Λ* to Λ is equal to 1:
In general, this is not equal to 1 although there are two special cases where this could occur. Firstly, either there are no price changes in the period, or secondly, the prices are moving in such a way that the denominator is equal to the numerator.
Back to table of contents11. References
Hirotugu Akaike. A new look at the statistical model identification. IEEE Transactions on Automatic Control, 19(6): pages 716 to 723, December 1974.
Bert M. Balk. Aggregation Methods in International Comparisons: What Have We Learned? June 2001.
Timothy K. M. Beatty and Ian A. Crawford. How Demanding Is the Revealed Preference Approach to Demand? American Economic Review, 101(6): pages 2782 to 2795, October 2011. doi: 10.1257/aer.101.6.2782. URL
Statistic Belgium. Consumer price index of January 2016 - Inflation rises to 1.74\% - Annual update of the index basket and increase in the use of scanner data, 2016.
Alan Bentley and Frances Krsinich. Towards a big data CPI for New Zealand, 2017.
Christian Blaudow and Florian Burg. Dynamic pricing as a challenge for Consumer Price Statistics, 2017.
Karola Brunner. Automated price collection via the internet. Wirtschaft und Statistik, 2014.
Robert Breton, Gareth Clews, Liz Metcalfe, Natasha Milliken, Christopher Payne, Joe Winton, and Ainslie Woods. Research indices using web scraped data, 2015.
Robert Breton, Tanya Flower, Matthew Mayhew, Elizabeth Metcalfe, Natasha Milliken, Christopher Payne, Thomas Smith, Joe Winton, and Ainslie Woods. Research indices using web scraped data: May 2016 update, 2016..
Antonio G. Chessa. A new methodology for processing scanner data in the Dutch CPI, Eurostat review on national accounts and macroeconomic indicators, 1/2016.
Antonio G. Chessa and Robert Griffioen. Comparing Scanner Data and Web Scraped Data for Consumer Price Indices, 2016.
Antonio G. Chessa, Johan Verburg, and Leon Willenborg. A Comparison of Price Index Methods for Scanner Data, 2017.
Gareth Clews, Anselma Dobson-McKittrick, and Joseph Winton. Comparing Class Level Chain Drift for Different Elementary Aggregate Formulae Using Locally Collected CPI Data, 2014.
Jan de Haan and Frances Krsinich. The treatment of unmatched items in rolling year GEKS prices indexes: evidence from New Zealand scanner data. 2012.
Jan de Haan and Heymeril A. van der Grient. Eliminating chain drift in price indexes based on scanner data. Journal of Econometrics, 161(1): pages 36 to 46, 2009.
Jan de Haan, Ren Hendricks, and Michael Scholtz. A Comparison of Weighted Time-Product Dummy and Time Dummy Hedonic Indexes. Gralz Economic Papers, 2016.
Rupert de Vincent-Humphreys. RPI and CPI: a tale of two formulae, 2017.
Gérard Debreu. Continuity properties of Paretian utility. International Economic Review, 5: pages 285 to 293, 1964.
Erwin Diewert. Hedonic Regression. A Consumer Theory Approach. Scanner Data and Price Indexes, 2003.
Lewis Edwards. VAT turnover, research analysis, UK: Jan 2014 to June 2016. 2017.
Heiđrún Erika Guđmundsdótti and Lára Guđlaug Jónasdóttir. Scanner Data: Initial Data Testing, 2016.
William T. Harbaugh, Kate Krause, and Timothy R. Berry. GARP for Kids: On the Development of Rational Choice Behavior. American Economic Review, 91(5): pages 1539 to 1545, December 2001. doi: 10.1257/aer.91.5.1539.
Lorraine Ivancic, W. Erwin Diewert, and Kevin J. Fox. Scanner data, time aggregation and the construction of price indexes. Journal of Econometrics, 161(1): pages 24 to 35, 2011.
Thomas H Jacobsen. Implementing scanner data in the Danish CPI, 2014.
Ingvild Johansen and Ragnhild Nygaard. Various data collection methods in the Norwegian CPI, 2012.
David W. Kalisch. Making Greater Use of Transactions Data to Compile the Consumer Price Index, Australia. 15th Meeting of the Ottawa Group, Eltville Am Rhein 2017, 2016. URL
David W. Kalisch. An implementation plan to maximise the use of transactions data in the CPI, 2017.
Frances Krsinich. FEWS index: Fixed Effects with a Window Splice, 2014.
Frances Krsinich. Price Indexes from Online Data Using The Fixed-Effects Window-Splice (FEWS) Index, 2015.
Frances Krsinich. The FEWS index: Fixed Effects with a Window Splice. Journal of Official Statistics, 32 (2): pages 375 to 404, 2016.
Claude Lamboray and Frances Krsinich. A modification of the GEKS index when product turnover is high, paper presented at the 14th meeting of the Ottawa group, Tokyo, 20 to 22 May 2015, 2015.
Sharon L. Lohr. Sampling: Design and Analysis. Duxbury Press, 1999.
Matthew Mayhew and Gareth Clews. Using Machine Learning Techniques To Clean Web Scraped Price Data Via Cluster Analysis. Survey Methodology Bulletin, 2016.
Elizabeth Metcalfe, Tanya Flower, Thomas Lewis, Matthew Mayhew, and Edward Rowland. Research indices using web scraped data: clustering large datasets into price indices (CLIP), 2016.
Reto Müller. Scanner data in the Swiss CPI: An alternative to price collection in the field, 2010.
J. Peter Neary and Brid Gleeson Comparing the Wealth of Nations: Reference Prices and Multilateral Real Income Indexes. The Economic and Social Review, 28(4): pages 401 to 421, October 1997.
ONS. Consumer Prices Indices - Technical Manual, 2014a.
ONS. Producer Price Indices - Methods and Guidance, 2014b.
ONS. Services Producer Price Indices - Methods and Guidance, 2015.
ONS. Research indices using web scraped data: clothing data, 2017.
Chris Payne. Analysis of product turnover in web scraped clothing data, and its impact on methods for compiling price indices, 2017.
Federico Polidoro, Riccardo Giannini, Rosanna Lo Conte, Stefano Mosca, and Francesca Rossetti. Web scraping techniques to collect data on consumer electronics and airfares for Italian HICP compilation. Statistical Journal of the IAOS, 31(2): pages165 to 176, 2015.
Guillaume Rateau, Implementation of the treatment of the scanner data in France, 2017.
Muhanad Sammar, Anders Norburg, and Can Tongur. Scanner Data - A Collection Method for the Future, 2012.
Mick Silver and Saeed Heravi. Why Elementary Price Index Number Formulas Differ: Price Dispersion and Product Heterogeneity. IMF Working Paper, 2006.
Jack Triplett. Handbook on Hedonic Indexes and Quality Adjustments in Price Indexes, 2006. doi: http://dx.doi.org/10.1787/9789264028159-en. URL
Back to table of contents