Table of contents
1. Abstract
The Office for National Statistics (ONS) in collaboration with the Southampton Statistical Sciences Research Institute (S3RI) has developed a methodology for estimating the uncertainty associated with the local authority mid-year population estimates. Measures of uncertainty for the 2002 to 2010 mid-year population estimates were published in 2012. Measures of uncertainty for the estimates for 2012 to 2016 are being published in 2017. This report provides information to support the interpretation of the estimates for the statistical measures of uncertainty for local authority districts in England and Wales in 2012 to 2016.
Development of a statistical measure of uncertainty is one of several projects established as part of the Migration Statistics Improvement Programme. The programme concluded in March 2012, but the implementation of improvements developed during its lifetime is an ongoing process. Specifically, these are research outputs and are an update to the 2012-2015 data series of published statistical measures of uncertainty associated with the mid-year population estimates. This series, 2012 to 2016, incorporates changes to the uncertainty methodology as a result of changes in the methods used to estimate international in-migration, which feeds into the mid-year population estimates.
Publication of the 2012 to 2016 uncertainty estimates provides an opportunity for users to assess their utility and give feedback.
Back to table of contents2. Acknowledgements
This project reflects the combined efforts of the ONS Demographic Methods Centre and the Southampton Statistical Sciences Research Institute (S3RI). ONS would particularly like to acknowledge the contribution of Professor Peter W.F. Smith from the University of Southampton.
Back to table of contents3. Introduction
The Uncertainty Project was established as part of the Migration Statistics Improvement Programme (MSIP 2008-12, ONS 2012a). Working in collaboration with Southampton Statistical Sciences Research Institute (S3RI), this project aimed to provide users of Office for National Statistics (ONS) local authority mid-year population estimates (MYEs) with more information regarding the uncertainty associated with these estimates.
The Uncertainty Project originally included 2 streams of work. The first involved the development of Quality Indicators, which was completed in 2012 (ONS 2012b). These show where local authorities are ranked on a short list of indicators: census base; international migration churn; internal migration churn; students; armed forces and cumulative net migration within rolled forward estimates. They are published annually with the MYEs.
The second stream, which is the focus of this guidance, was to produce a cumulative statistical measure of uncertainty for local authority MYEs. We published measures of uncertainty for the 2002 to 2010 MYEs as research outputs in 2012 (ONS 2012c). The methods have been adapted following the 2011 Census to reflect changes in the methodology to produce estimates of in-migration, which feed into the MYEs. The research report (ONS 2017) published alongside this guidance updates the 2012 research report that was published (ONS 2012c and ONS 2012d) with the 2002 to 2010 series. We welcome your feedback, both on the methods used and the results of this research.
Within this project, “uncertainty” is understood as the quantification of doubt about a measurement. Early research indicated that, of the components used to derive the MYEs, the 3 that contributed most to uncertainty were the census base, international and internal migration. Uncertainties associated with these 3 components have been combined into a single composite measure of uncertainty. Provided as measures of dispersion (the relative root mean squared error between simulated estimates and the MYE, as a proportion of the mean value of the simulations), this composite measure of uncertainty only includes uncertainty from these 3 components. As such, it represents a conservative measure of the total uncertainty in the estimates.
Principle 4 of the Code of Practice for Official Statistics (UK Statistics Authority 2009) states that users should be informed about the quality of statistical outputs. While complying with this instruction, the greater motivation for developing the statistical measures of uncertainty was to provide information that assists users in their decision-making. For example, the provision of uncertainty ranges for the MYEs and information on the relative contributions from the 3 components could assist local authorities in prioritising, fine tuning and building in appropriate contingency when allocating services and resources. They also provide us with information about the quality of the estimates and their constituent parts, over time.
You are encouraged to provide feedback to us on these estimates, in particular in terms of their usefulness and to express your views concerning future provision of measures of uncertainty. This can be done by email to popinfo@ons.gov.uk.
Back to table of contents4. Methodology
The methodology for deriving the statistical measures of uncertainty is described in detail in the accompanying report (ONS 2017). Here we provide a brief summary of the methodology for each component and for the composite.
The mid-year population estimates (MYEs) are derived using a cohort component method (see Jefferies and Fulton 2005 for details). In brief, components of demographic change (natural change (births less deaths), net international migration and net internal migration) are added to the previous year’s aged-on population. As well as adding the net components of change, additional procedures are applied to account for special populations (for example, armed forces, school boarders, prisoners).
Initial work (ONS 2010) identified the census base, international migration and internal migration as the 3 components used during derivation of the MYEs with the greatest impact on uncertainty. Consequently, the statistical measure of uncertainty for local authority MYEs is a composite of uncertainty associated with these 3 components only.
As uncertainty or error can arise from both data sources and the processes used to derive the MYEs, the general approach for measuring uncertainty is to use observed data and recreate the MYEs’ derivation processes for the 3 components many times (1,000) to simulate a range of possible values that might occur. Due to differences in data sources and procedures used to derive each component of the MYEs, there are some differences in the methods used to generate the simulated distributions for each of the components (see ONS 2017 for details).
A simulation method that replicates the cohort component method for deriving the MYEs is used to combine these simulated distributions with the other components of change that are assumed to have zero error (for example, births and deaths). As with the MYEs themselves, the simulated estimates are rolled forward each year through the 10 year inter-censal period. This ensures that the simulated distribution for the composite includes both the uncertainty carried forward from previous years and the new uncertainty for the current year. In this way the uncertainty associated with the 3 components (the census base, international migration and internal migration) is taken into account to produce a simulated distribution of plausible estimates for each local authority for each year.
The principal uncertainty measure is the root mean squared error (RMSE). The RMSE is the variability of the simulated values around the MYE. When the RMSE is calculated as a percentage of the mean simulated composite measures, this becomes the relative root mean squared error (RRMSE). We have standardised our figures to the 2011 Census estimate for each local authority, to support comparisons over time and across local authorities. We also provide the proportional contribution that each component (2011 Census, internal migration and international migration) makes to the primary uncertainty measure.
We have identified and supplied 3 methods for deriving 95% confidence intervals for the published MYEs. Our preferred method is the bias-adjusted confidence intervals, but we supply all 3 to support your understanding of our methodological approach and of the options available:
Empirical confidence intervals
Empirical confidence intervals for each local authority are created by ranking the 1,000 simulated values of the population estimate and taking the 26th and 975th values as the lower and upper bounds respectively. As the observed MYE generally differs from the median of the simulations, this confidence interval is not centred about the MYE and in some extreme cases the MYE is outside the bounds of the empirical 95% confidence interval.Centred empirical confidence intervals
Centred empirical confidence intervals are created by moving the empirical 95% confidence intervals so that they are centred about the observed MYEs. The difference between the median of the simulated values and the observed MYE is subtracted from each of the lower and upper bounds. While the width of the confidence interval remains the same it does not account for the bias component due to the difference between the MYE and the median of the simulation.Bias-adjusted confidence intervals
Bias-adjusted confidence intervals are calculated as the mid-year estimate plus or minus 1.96 multiplied by RMSE. The RMSE is the variability of the simulated values around the MYE. This confidence interval will be symmetric about the MYE and will include a measure of uncertainty due to bias between the MYE and the simulations.
We favour the bias-adjusted confidence interval because it is wider, reflecting the difference between the published MYE and the mean of the simulated composite measures. The discrepancy between the published MYE and the mean of the simulated composite measures may arise for a number of reasons, including:
the uncertainty methodology only accounts for uncertainty in the census, international and internal migration components
the assumptions underlying the uncertainty or mid-year estimates methodology
the uncertainty figures are estimates and so also contain uncertainty themselves
We have also specifically identified the undercounting of young males in the internal migration component of the MYEs, to help explain this discrepancy.
We interpret the bias-adjusted confidence intervals in the following way. If the assumptions we have made in estimating uncertainty are correct, we would expect these intervals on average to capture the mid-year population 95% of the time. However, if the bias is relatively large then these confidence intervals will be conservative, i.e., have coverage greater than 95%. Use and interpretation of the confidence intervals will be reviewed as we approach the 2021 census when uncertainty around the MYEs is at its highest level.
Back to table of contents5. The measures of uncertainty
Spreadsheet 1: Measures of uncertainty with proportional contributions
The statistical measures of uncertainty for each local authority are presented in the spreadsheet Measures of uncertainty with proportional contributions, published with this guidance. Data from the table are also used to create interactive maps, which allow a visual representation of the relative uncertainty for each local authority in England and Wales, for each year.
The “Uncertainty measures” sheet includes:
the published mid-year population estimates (MYE)
uncertainty measure (percentage of population) (the relative root mean squared error (RRMSE))
the percentage contribution of each component (2011 Census, internal migration, international migration) to the uncertainty measure
the upper and lower bounds of the bias-adjusted confidence intervals (the empirical and centred confidence intervals are also supplied in an interactive spreadsheet)
The “Proportional contributions” sheet includes interactive charts showing the contributions that each component makes to uncertainty in a selected local authority in each year 2012 to 2016.
Spreadsheet 2: Measures of uncertainty – all confidence intervals
The “Bias-adjusted confidence interval time series” sheet shows the 2012 to 2016 bias-adjusted confidence intervals and MYEs for each local authority.
The “All CI time series in the spreadsheet” sheet shows all 3 confidence intervals for 2012 to 2016, along with the respective MYEs.
The “Absolute confidence intervals“ sheet presents the confidence intervals in a non-standardised form. These are the raw data that underpin the charts in the rest of this spreadsheet.
Several points to bear in mind when interpreting the uncertainty measures are:
uncertainty values in the spreadsheet rely on assumptions made in the methodology and are research outputs, intended to provide the basis for discussion
the uncertainty estimates are conservative and only include potential error associated with the following 3 components of change in the MYEs: census, international and internal migration
the methodology assumes zero error for natural change (births and deaths) and other minor components such as constraining the Patient Register to the NHS Central Register (used in internal migration processing)
the methodology takes into account uncertainty as a result of imputation in the International Passenger Survey
the statistical measure of uncertainty does not include uncertainty associated with other adjustments used to derive the MYEs (for example, asylum seekers and dependants, prisoners, armed forces); the methodology assumes that error associated with these adjustments is relatively insignificant and assumes no error
5.1 Interpreting the “Measures of uncertainty with proportional contributions spreadsheet”
The “Uncertainty measures” sheet
This spreadsheet presents values for all local authorities and years 2012 to 2016. The uncertainty measure, the 95% bias-adjusted confidence interval and the proportional contribution that each component makes to the combined uncertainty are provided. Results for Derby, Leicester and Rutland provide useful comparisons for this guidance and are shown in Table 5.1.
Table 5.1: Sample of the uncertainty measures and proportional contributions spreadsheet
| 2012 East Midlands example | ||||||||
| Area names | Local Authority Code | Uncertainty measure (%) | % contribution 2011 Census | % contribution international migration | % contribution internal migration | Bias-adjusted confidence interval lower bound | Bias-adjusted confidence interval upper bound | Mid-year estimate |
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) |
| Derby | E06000015 | 1.30 | 97 | 2 | 2 | 244,154 | 256,982 | 250,568 |
| Leicester | E06000016 | 1.20 | 82 | 15 | 4 | 323,831 | 339,381 | 331,606 |
| Rutland | E06000017 | 0.91 | 78 | 4 | 19 | 36,359 | 37,671 | 37,015 |
| Source: Office for National Statistics | ||||||||
Download this table Table 5.1: Sample of the uncertainty measures and proportional contributions spreadsheet
.xls (27.6 kB)Column (1) – Area names:
The 348 local authority districts in England (in 9 regions) and in Wales.
Column (2) - Local authority code the 9-character Government Statistical Service code for local authority districts, the first 3 characters denoting:
E06 Unitary authorities
E07 Non-metropolitan districts
E08 Metropolitan districts
E09 London boroughs
Column (3) - Uncertainty measure (percentage of population):
The principal uncertainty measure is the root mean squared error (RMSE). The RMSE is the variability of the simulated values around the MYE. The higher the value, the wider the spread of values about the MYE and the greater the uncertainty. When the RMSE is calculated as a percentage of the mean simulated composite measures, this becomes the relative root mean squared error (RRMSE). Table 5.1 shows that for the 3 local authorities listed, uncertainty in 2012 is highest for Derby and lowest for Rutland.
Columns (4), (5) and (6) - Percentage contribution - 2011 Census; ….international migration; …internal migration:
These 3 columns provide the percentage contribution from each of the 3 components to the overall uncertainty for the local authority. These figures are percentages of the combined uncertainty, not of the local authority population. They have been rounded, so may not sum to 100.
These percentage contributions are relative and will vary over time. Uncertainty from international and internal migration includes accumulated uncertainty from previous years rolled forward, plus new uncertainty for the given year.
Columns (7) and (8) - Bias-adjusted confidence intervals, lower and upper bounds:
The lower and upper bounds denote the beginning and end of the bias-adjusted 95% range.
This confidence interval is symmetrically distributed around the MYE and adjusts for the difference between the mean of the simulated composite measure and the MYE (see the Methodology for Measuring Uncertainty in ONS Local Authority Mid-year Population Estimates: 2012 to 2016, ONS 2017, for details).
Column (9) - Mid-year estimate:
This is the local authority population MYE as published by the Office for National Statistics (ONS) for that year.
Proportional contributions charts
This chart allows you to view how the proportional contribution to uncertainty provided by each of the 3 components (census, international and internal migration) changes between 2012 and 2016. You can select a local authority using the drop-down menu and the chart displays the proportional contributions of each component for each year for the selected local authority.
Figures 5.1 to 5.3 show the proportional contribution charts for Derby, Leicester and Rutland, as examples. Results for these local authorities provide useful comparisons for this guidance. They also illustrate differences in the contribution of each component to the overall uncertainty for that local authority.
In all 3 local authorities in 2012, most of the uncertainty comes from the 2011 Census. The proportion of uncertainty that is attributed to the census declines over time as the cumulative uncertainty from previous years in the international and internal migration components are rolled forward, while the uncertainty derived from the census base remains the same. By 2016, the 2011 Census continues to be the main source of uncertainty in the MYE for Derby, while for Leicester, international migration contributes the most. In Rutland, internal migration now contributes more to uncertainty than the census (48% for internal migration compared with 38% for census).
Figure 5.1: Proportional contributions to uncertainty from the 2011 Census, international and internal migration in Derby
E06000015 Derby
Download this chart Figure 5.1: Proportional contributions to uncertainty from the 2011 Census, international and internal migration in Derby
Image .csv .xls
Figure 5.2: Proportional contributions to uncertainty from the 2011 Census, international and internal migration in Leicester
E06000016 Leicester
Download this chart Figure 5.2: Proportional contributions to uncertainty from the 2011 Census, international and internal migration in Leicester
Image .csv .xls
Figure 5.3: Proportional contributions to uncertainty from the 2011 Census, international and internal migration in Rutland
E06000017 Rutland
Download this chart Figure 5.3: Proportional contributions to uncertainty from the 2011 Census, international and internal migration in Rutland
Image .csv .xls5.2 Interpreting the “Measures of uncertainty - all confidence intervals” spreadsheet
“Bias-adjusted confidence intervals time series” sheet
This sheet presents the 2012 to 2016 bias-adjusted confidence intervals, shown as a percentage of the 2011 Census estimate for each local authority. Standardising the bias-adjusted confidence intervals in this way allows them to be compared across local authorities. The chart displays, for a selected local authority, the standardised bias-adjusted confidence intervals and the standardised published MYEs for 2012 to 2016. Figures 5.4 to 5.6 show the standardised bias-adjusted confidence intervals for Derby, Leicester and Rutland, as examples.
Figures 5.4 to 5.6 show the bias-adjusted confidence interval width and therefore the statistical uncertainty around the MYE, increasing for all 3 local authorities between 2012 and 2016. In 2012, the local authority with the widest confidence interval relative to its 2011 Census population and therefore the greatest relative uncertainty in the 2012 MYE, was Derby. Most of the uncertainty in Derby in 2012 derives from the 2011 Census component (see Figure 5.1). By 2016, the bias-adjusted confidence interval is widest (relative to its 2011 Census population) for Rutland. By 2016, internal migration makes the largest proportional contribution to uncertainty in Rutland (see Figure 5.3).
Figure 5.4: Standardised bias-adjusted confidence intervals for Derby
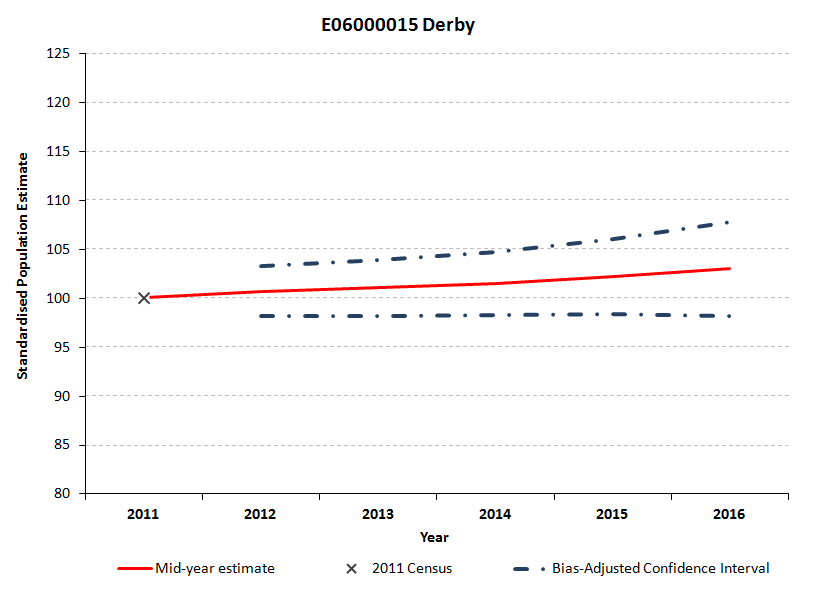
Download this image Figure 5.4: Standardised bias-adjusted confidence intervals for Derby
.png (19.3 kB)
Figure 5.5: Standardised bias-adjusted confidence intervals for Leicester
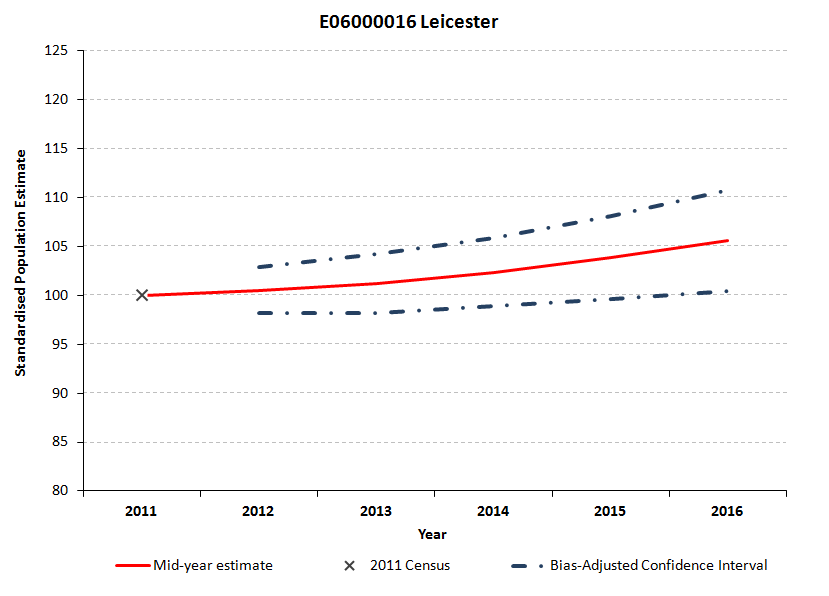
Download this image Figure 5.5: Standardised bias-adjusted confidence intervals for Leicester
.png (20.4 kB)
Figure 5.6: Standardised bias-adjusted confidence intervals for Rutland
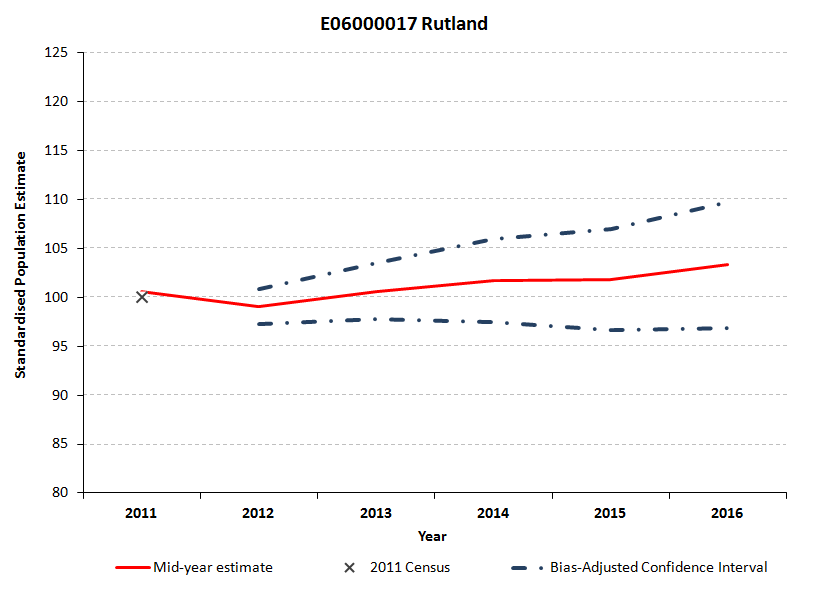
Download this image Figure 5.6: Standardised bias-adjusted confidence intervals for Rutland
.png (20.6 kB)“All confidence interval time series” sheet
This sheet presents all 3 confidence intervals for 2012 to 2016, standardised to the 2011 Census estimate for each local authority to support comparisons between local authorities. The Methodology for Measuring Uncertainty in ONS Local Authority Mid-year Population Estimates: 2012 to 2016 (ONS 2017) report describes the confidence intervals:
empirical confidence intervals
bias-adjusted confidence intervals
centred empirical confidence intervals
The interactive chart shows, for the selected local authority, all 3 confidence intervals and the published MYEs for 2012 to 2016. Figures 5.7 to 5.9 show the standardised confidence intervals and the MYEs for Derby, Leicester and Rutland for years 2012 to 2016.
Figure 5.7: Standardised empirical, bias-adjusted and centred empirical confidence intervals for Derby
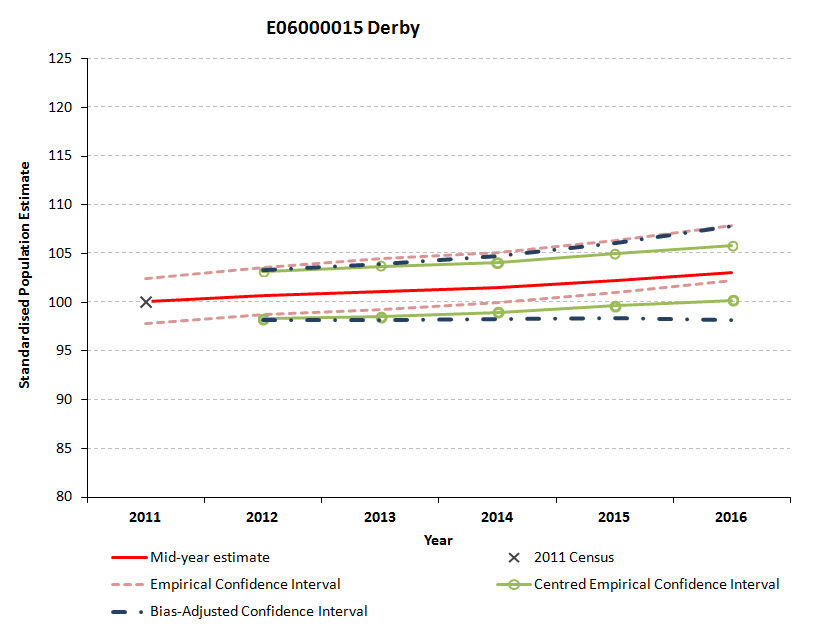
Download this image Figure 5.7: Standardised empirical, bias-adjusted and centred empirical confidence intervals for Derby
.png (31.7 kB)
Figure 5.8: Standardised empirical, bias-adjusted and centred empirical confidence intervals for Leicester
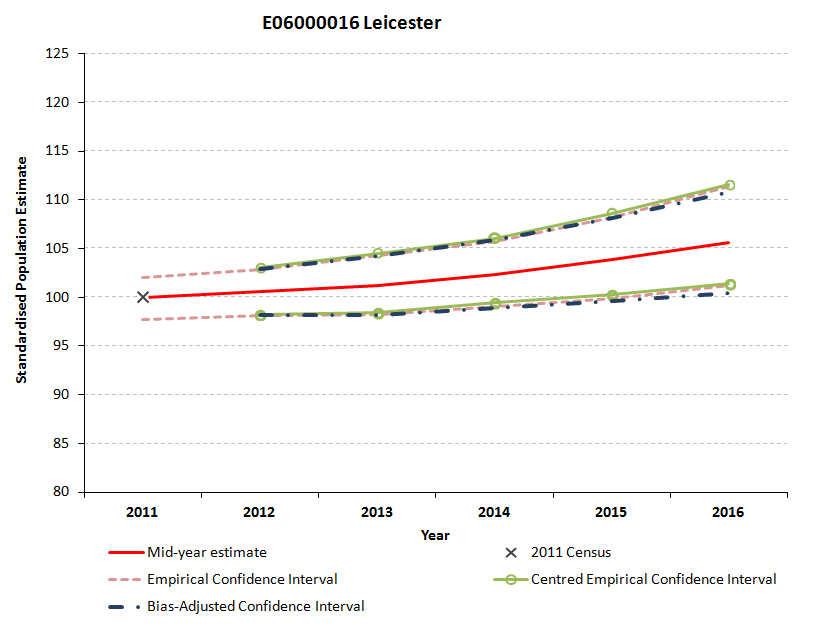
Download this image Figure 5.8: Standardised empirical, bias-adjusted and centred empirical confidence intervals for Leicester
.png (33.1 kB)
Figure 5.9: Standardised empirical, bias-adjusted and centred empirical confidence intervals for Rutland
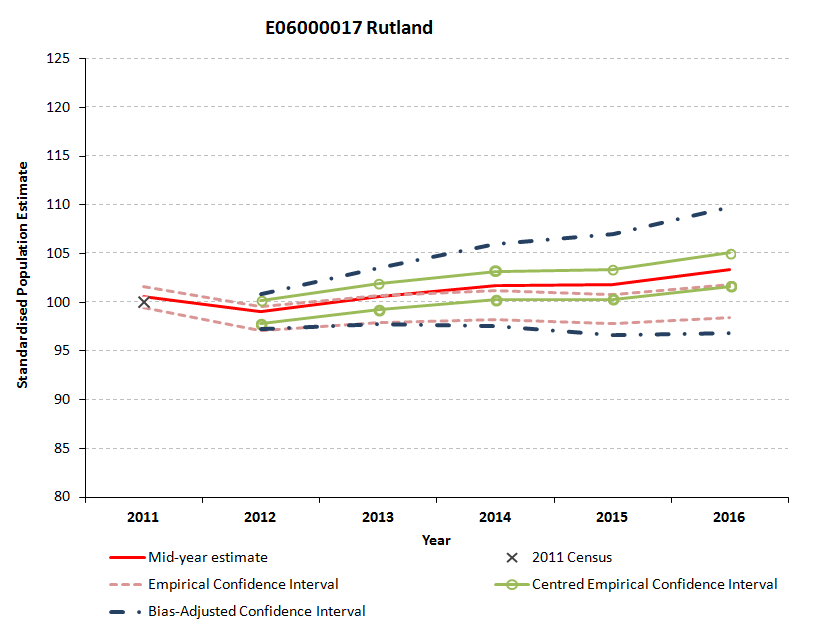
Download this image Figure 5.9: Standardised empirical, bias-adjusted and centred empirical confidence intervals for Rutland
.png (33.5 kB)In Figure 5.8, the 3 confidence intervals for Leicester are very close. By contrast, in Figure 5.7 for Derby the empirically-derived confidence intervals are asymmetric around the MYE. The centred empirical confidence interval and the bias-adjusted interval are at the centre of the distribution, because they are calculated in a way that ensures this. The bias-adjusted confidence interval, our preferred measure, is wider, for the reasons listed in Section 2 “Methodology”.
In Figure 5.9 for Rutland, the empirically-derived standardised confidence intervals are also asymmetric around the published MYEs in 2012. By 2014, the MYE is outside of the empirically-derived confidence interval, which suggests that the range of uncertainty has been under-estimated. By definition, the MYE sits within the range of uncertainty for both the centred empirical and bias-adjusted confidence intervals, though the bias-adjusted interval is wider than the centred one, reflecting the discrepancy between the MYE and the mean of the simulated composite measures.
“Absolute confidence intervals” sheet
The standardisation of the charts in the “Bias-adjusted confidence interval time series” and “All confidence interval time series” sheets allows users to compare uncertainty across local authorities, because in each case the confidence interval is expressed as a proportion of the local authorities’ 2011 Census population. The absolute values in this sheet allow comparison of the absolute sizes of the confidence intervals between local authorities. Thus we found in the other sheets that Rutland has the widest (standardised) confidence interval compared with Leicester and Derby. However, the absolute values reveal that Rutland has a much smaller population than the other 2 local authorities (38,606 in Rutland, 256,233 in Derby and 348,343 in Leicester in 2016). The confidence intervals are correspondingly smaller, in absolute terms.
5.3 Interactive maps
Interactive maps are provided with the outputs. The maps allow readers to select the local authority and the maps display the uncertainty measures (percentage population) for each year 2012 to 2016, with colour coding.
Back to table of contents6. References
Jefferies, J. and Fulton, R. (2005). Making a Population Estimate. NS Methodology Series No.34.
Office for National Statistics (2010). Improving Migration and Population Statistics - Quality measures for population estimates.
Office for National Statistics (2012a). Migration Statistics Improvement Programme.
Office for National Statistics (2012b). Uncertainty in local authority mid-year population estimates.
Office for National Statistics (2012c). Methodology for deriving a statistical measure of uncertainty 2001-12.
Office for National Statistics (2012d). Guidance on interpreting the statistical measures of uncertainty.
Office for National Statistics (2017). Methodology for measuring uncertainty in ONS local authority mid-year population estimates: 2012 to 2016.
UK Statistics Authority (2009). Migration Statistics: The Way Ahead.
Back to table of contentsContact details for this Methodology
You might also be interested in:
- Measures of statistical uncertainty summary
- Methodology for measuring uncertainty in ONS local authority mid-year population estimates: 2012 to 2016
- Measures of uncertainty - all confidence intervals
- Measures of uncertainty with proportional contributions
- Population estimates
- Population estimates: quality information
