Measures of statistical uncertainty in ONS local authority mid-year population estimates: England and Wales, 2020

• Incorporating the merging of local authorities
• Changes to the international migration component

Measures of statistical uncertainty for the local authority mid-year population estimates (MYEs) are research statistics that aim to give users of MYEs information about their quality. Uncertainty measures for 2011 to 2019 were published in 2020. These were produced for each of the then 348 local authorities in England and Wales.

The complexity of the MYE methodology makes it impossible to estimate this uncertainty directly. The methodology described in Methodology for measuring uncertainty in ONS local authority mid-year population estimates: 2012 to 2016, quantifies uncertainty and indicates the relative contribution to this uncertainty by each of the three components that impact on uncertainty the most: the 2011 Census base, international and internal migration.

In this article we extend the time series to 2020. We also incorporate changes made to the geographical boundaries of local authorities in 2019 and 2020. We temporarily changed our methodology for calculating international migration uncertainty because of computational issues encountered in implementing the method.

In this article we provide empirical 95% uncertainty intervals. If the assumptions we have made in estimating uncertainty are correct, we would expect these intervals on average to capture the true population 95% of the time.

The uncertainty methodology is based on three components with the greatest impact on uncertainty. The measures do not incorporate the uncertainty associated with all of the data sources and processes involved in producing MYEs and should be considered to be conservative.

The coronavirus (COVID-19) pandemic has had an impact on the data quality of some of the sources feeding into both the mid-year estimates and their uncertainty. The International Passenger Survey (IPS), the main source of the international migration component, was suspended in March 2020 but reinstated in January 2021. To overcome the absence of IPS data from March to June 2020, measures of LTIM were modelled to estimate UK international migration.

Incorporating the merging of local authorities

The three main sources of uncertainty associated with the mid-year population estimates (MYEs) are the census base, international migration, and internal migration (moves between local authorities (LAs)). Uncertainty in the other components of change (births, deaths, asylum seekers, armed forces, and prisoners) is assumed to be zero.

The methodology for producing internal migration uncertainty has remained the same for local authorities whose geographic boundaries have not changed in recent years. Further details on this process can be found in Methodology for measuring uncertainty in ONS local authority mid-year population estimates: 2012 to 2016. In 2019 and 2020, a number of local authorities merged into new ones. Table 1 outlines which local authorities were affected. Because of certain features intrinsic to the internal migration methodology, it is not possible to process them the same as other local authorities.

We calculated the relative width and position of the uncertainty intervals for each LA in the newly merged LAs. We combined them into a weighted average to produce uncertainty intervals for the 2020 MYE in the following manner:

1.

Where MYE₂₀₁₉ is the 2019 mid-year estimate, LB₂₀₁₉ is the lower bound of the uncertainty interval for the 2019 mid-year estimate, UB₂₀₁₉ is the corresponding upper bound, and x_XB are the corresponding relative uncertainty bounds.

The relative uncertainty bounds for the merged LAs are calculated as a weighted average of those of its constituent LAs:

3.

Where x_i is the relative uncertainty bound for LA_i and w_i is the proportion of the population in LA_i and x_T is the relative uncertainty bound for the merged LA. Equation 3 is calculated separately for the lower and upper bound of the mid-year estimate.

The relative uncertainty bounds for the 2020 mid-year estimates are then calculated as:

4.

This was calculated for all local authorities in Table 1.

Changes to the international migration component

We use bootstrapping to simulate uncertainty around the international migration component, however this was not possible because of computational issues encountered in implementing the method. Instead, we use the international migration point estimate and uncertainty interval from 2011 to 2019 for each LA. This is to identify patterns in the widths of the intervals and the position of the point estimate in the interval over time. No specific patterns were found. Therefore, we calculate the relative width of the 2019 uncertainty intervals and apply to the 2020 MYE for the international migration component.

The estimates for the 2020 international migration component are based on the International Passenger Survey (IPS) data up to March 2020, and modelled migration estimates for the period after March 2020 when the IPS was suspended because of coronavirus (COVID-19). Figure 1 summarises the changes that have been made to produce the 2020 mid-year estimate uncertainty.

Figure 1: 2020 mid-year estimate cohort component method and statistical uncertainty

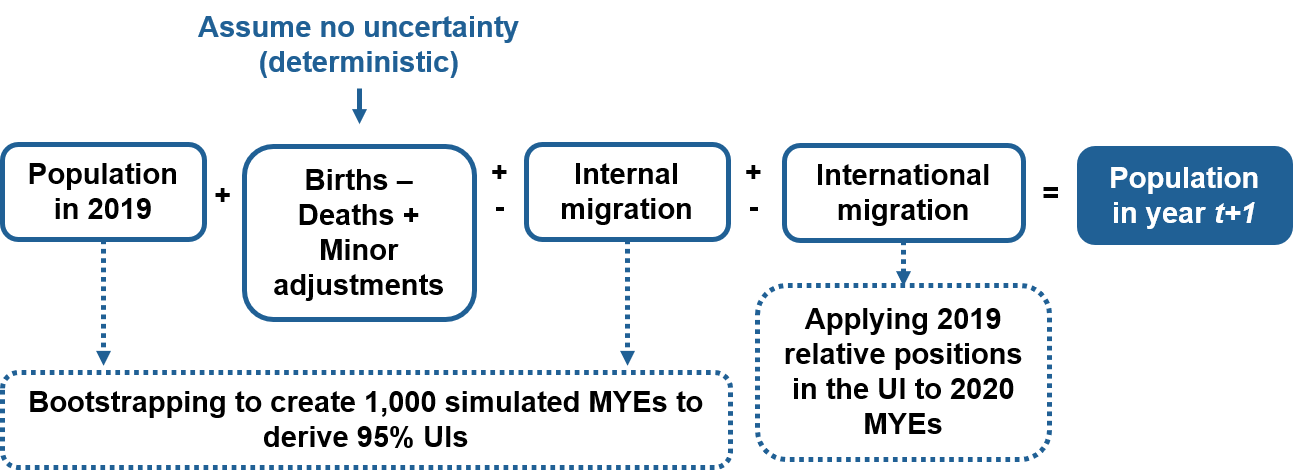
Source: Office for National Statistics

Download this image Figure 1: 2020 mid-year estimate cohort component method and statistical uncertainty

.png (30.7 kB)

We produce uncertainty intervals for all local authorities in England and Wales.

Table 2 shows that for most local authorities, the mid-year population estimates (MYEs) no longer sit within its uncertainty interval in 2020.

Over time, a growing number of local authority MYEs fall outside of their empirical 95% uncertainty bounds. By 2020, this is the case for 161 local authorities. This is consistent with our understanding that estimation of the population becomes progressively more difficult as we move away from the census.

Table 3 outlines how the local authorities are interacting with the uncertainty interval. Figures 2 to 7 provide illustrative examples of local authorities for each position in this table.