Table of contents
- Main points
- Introduction
- Drivers for the methodological review
- Section A: Quality of high-age population estimates input data
- A1. Deaths data
- A2. Quality of Census data at older ages
- A3. Quality of migration data at older ages
- Section B: How good is the Kannisto-Thatcher (KT) method?
- B1. Description of the KT method of calculation
- B2: Accuracy
- B3: Population modelling
- Section C: Comparisons to counts derived from administrative data
- Overall summary and conclusions
- Background notes
1. Main points
It is a legal requirement for all deaths occurring in England and Wales to be registered so these deaths data can be taken as complete.
Deaths data is of very high quality in terms of accuracy of age at death for those dying at ages 105 and over in England and Wales who were born in England and Wales.
There is a high degree of accuracy in birth data (and derived age) in census records for those aged 80 and over in the Office for National Statistics Longitudinal Study (ONS-LS) sample. Given that the ONS-LS is a representative sample of the 2011 Census records, this implies that there is a high degree of accuracy in the birth data of those aged 80 and over in the 2011 Census as a whole.
Year of birth recorded in the 2011 Census was not the modal (most common) year of birth across all available records for 1.1% of cases for those aged 80 and over in the ONS-LS. The reliability of the 2011 Census year of birth data decreased with age (for the 80 and over age group).
Levels of both UK cross-border migration and international migration at the oldest ages are very low. Migration, therefore, has minimal impact on the annual mid-year estimate of those aged 90 and over.
The KT method assumes minimal migration at the oldest ages. This assumption appears to hold true. However, if migration at the oldest ages grows, the performance of the method will deteriorate.
The KT method works well where the deaths data are in the correct format and mortality rates at the oldest ages are not changing over time. Where mortality rates are changing over time at the oldest ages, a different method for allowing for changes in mortality in the KT methodology may produce better estimates.
Official estimates of the age 90 and over population are higher than SPD V1.0 estimates and SPD V1.0 estimates are generally higher than KT estimates (before constraining to the official MYE age 90 and over total) at the 4 time points available. Age distributions of the age 90 and over population in the 3 data sources are very similar.
Back to table of contents2. Introduction
Increasing numbers of people are living to very old ages (90 and over). This has led to growing interest in obtaining accurate estimates of population numbers and mortality rates by single year of age at these ages.
In England and Wales there were estimated to be 504,030 people aged 90 and over in 2015 (0.9% of the total population). This compares with 222,820 (0.4% of the total population) in 1991. By 2039, the population aged 90 and over is projected to reach 1,516,130 (2.3% of the total population) and deaths at age 90 and over are projected to rise from 22% of all deaths in 2015 to 34% in 20391.
We are undertaking a review of the methods used to obtain high-age population estimates and the quality of the underlying input data.
This report gives an overview of the population and deaths data available to us and an assessment of its quality; the methods used to construct population estimates at ages 90 and above and the results of the review to date. Some recommendations for possible improvements are made and further research to be undertaken outlined. These were presented and discussed with users at a workshop held in March 2016.
This report is confined to consideration of the accuracy of high-age population estimates for England and Wales as a whole only.
Notes for: Introduction
- This text was changed on 13 December 2016 to the 90 and over population estimate for 2015 for England and Wales as the 90 and over population estimate for 2015 for the UK was quoted in the original publication. Additionally the projected proportion of deaths attributable to the 90 and over population in 2039 was amended.
3. Drivers for the methodological review
In recent years, the accuracy of official high-age estimates has been debated and questioned by some expert users1. The 2011 Census suggested there were around 30,000 fewer people aged 90 and over than had been estimated by rolling forward the 2001 Census data to 2011. (A proportionally small overestimation in the number of 80 to 89-year-olds in 2001 would result in a much larger proportional overestimation in the number of those aged 90 and over by 2011.)
The UK Statistics Authority is currently undertaking an assessment of the annual Estimates of the Very Old data series (population estimates of those aged 90 and over by single year of age up to age 105 and over). The UK Statistics Authority reassesses outputs that have National Statistics status periodically to ensure they meet users’ needs.
Correctly estimating the high-age population is important for our other outputs including population projections, life expectancy and mortality rates and mortality improvements. All of these have significant policy implications, including health and social care planning, resource allocation and state and private pension provision.
Understanding the accuracy of high-age population estimates is also important for 2021 Census planning and the development of future population estimation methods.
We have 2 independent methods of estimating the size of the population aged 90 and over: estimates derived from rolling forward the decennial census figures; and population estimates of those aged 90 and over reconstructed from deaths data. There are also a number of administrative data sources available with counts of people aged 90 and over. We are conducting research to assess the quality of these data and to explore whether administrative data can be used in the production of population estimates in the future.
The decennial census provides the basis for the mid-year estimates (MYE) of the population for England and Wales. These are annual population estimates by sex and single year of age up to age 89 and for the 90 and over age group. They are produced by rolling the census estimates forward allowing for ageing, births, deaths and migration (the cohort component method).
Estimates of the very old, including centenarians (EVOs) are produced from death registration data using a version of survivor-ratio methodology, the Kannisto-Thatcher (KT) method. These are annual estimates by sex and single year of age for people aged 90 to 104 and for the 105 and over age group for England and Wales. To provide users with a consistent set of estimates by single year of age up to age 105 and over, EVOs are constrained to the 90 and over totals in the MYE.
The official MYE of the 90 and over population and the 90 and over population estimate obtained from the KT methodology do not tally (prior to constraining the KT 90 and over total to the MYE 90 and over total). In a typical year the estimate of the population aged 90 and over obtained from KT methodology is lower than the official MYE.
The accuracy of the MYE of the 90 and over population is wholly dependent on the quality of the input data. If the census estimates and the annual death and net migration figures were completely accurate then the MYE of the age 90 and over population would by default be accurate.
The accuracy of the KT estimate of the age 90 and over population is dependent both on the quality of the input death data and the robustness of the KT methodology.
Section A of this report examines the quality of the input data for high-age population estimates – death registration data, census estimates and migration data. The KT methodology is described and reviewed in Section B. In Section C of the report, KT estimates of the age 90 and over population are compared with counts derived from administrative sources. The final section of the report outlines planned further research on the accuracy of high-age estimates.
Notes for Drivers for the methodological review
- Cairns, Andrew J. G. and Blake, David P. and Dowd, Kevin and Kessler, Amy R., Phantoms Never Die: Living with Unreliable Population Data (December 21, 2014). Journal of the Royal Statistical Society, 2016. Richard Willets (2012) Longevity and our 'missing' 90-year-olds, The Actuary:
4. Section A: Quality of high-age population estimates input data
Introduction
The age 90 and over total population estimate in the annual mid-year population estimates (MYE) is the census estimate of those aged 90 and over (aged on) minus deaths, plus net migration. The quality of the MYE of those aged 90 and over is therefore dependent on the quality of the census estimate, deaths data and migration data at the oldest ages.
Population estimates of those aged 90 and over by single year of age are produced from deaths data using a form of survivor-ratio methodology, the Kannisto-Thatcher (KT) method (see Section B).
In this section the quality of deaths data used in the production of high-age estimates is assessed.
Back to table of contents5. A1. Deaths data
A1. Deaths data
Deaths data collection
Mortality data and statistics for England and Wales are based on the details collected when deaths are certified and registered. Most deaths in England and Wales are certified by a medical practitioner who will issue a Medical Certificate of Cause of Death (MCCD). This will be taken to a Registrar, usually by a relative of the deceased.
Deaths occurring in England and Wales should be registered within 5 days of the date of death. However, in certain cases deaths are referred to, and sometimes then investigated by, a coroner resulting in a delay to the registration of the death1. (The death cannot be registered until all investigations are complete. While delays are commonly only a few days, they can extend into years.) In such cases, the coroner sends information to the Registrar, and this is used instead of that on the MCCD to register the death.
The information recorded at death registration is cause of death (taken from the MCCD or the coroner’s certificate); the date of birth and date of death (used to derive the age at death), sex, marital status, occupation and usual residence. These details are supplied by the informant except after an inquest when the coroner will supply the age and sex of the deceased.
Quality of deaths data
Doctors are given guidance on completing MCCDs in England and Wales by the Department of Health (DH) under the Coroner and Justice Act 2009. The guidance was last updated in July 2010 and is being reviewed and updated as part of the proposed changes to death certification process in England and Wales. New guidance will be issued by DH following the implementation of the planned reforms. This guidance will be agreed by DH, the Office for National Statistics (ONS), General Register Office (GRO) and the National Medical Examiner when appointed.
Data items other than cause of death depend largely on information supplied by the informant. Registrars are instructed to make a number of checks including that the correct medical certificate has been used and refers to the correct person and that the informant is qualified to give information. Details supplied are also checked for reasonableness, for example, age and cause of death. The details are entered directly onto the Registrations Online (RON) system. Automated checks such as valid ranges and the logical consistency of data are built into RON.
We receive death registration details from the register offices electronically on a daily basis. Automated validation checks are carried out on each file received to ensure there is no interruption in the flow, for example, checks for invalid characters or records where mandatory fields were not populated. Combined deaths data are then loaded onto the deaths database and another series of automated and manual checks carried out to identify any discrepancy in the data, highlighting registrations where date of birth, date of death or cause of death were recorded incorrectly. Several diagnostic checks take place on a weekly and monthly basis to identify quality issues, for example, duplicates and missing entries and whether, during the coding process, correct values were assigned, ensuring the optimal completeness and accuracy of stored registration data is achieved.
Death details that require coding such as occupation, usual residence and cause of death are then coded. The majority of this coding is automated, for example, 70% of occupation data and 80% of cause of death data are coded automatically. However, some data needs to be coded manually by specialised coders, for example, inquest deaths and adjournments are coded manually due to the formatting of the cause text. The accuracy of automated coding is checked regularly.
Further checks are made before and after extraction of data for analysis, for example, frequency checks to ensure distributions are plausible and broadly similar to previous years3.
Age at death validation
When a death is registered, an informant is asked to supply the date of birth of the deceased. This is not cross-checked with birth records. Age at death, as published in death statistics, is derived by subtracting the date of birth supplied by the informant from the date of death. An incorrect age at death in the statistics could therefore be assigned if either the date of birth or the date of death is incorrectly supplied to, or incorrectly recorded by, the Registrar. In England and Wales, the 5-day time limit for registering a death after it has occurred (except in the case where a death has been referred to a coroner) should mean that the date of death will only rarely be incorrect. Input errors should be very rare as the informant is asked to check the data inputted by the registrar. If the informant doesn’t know the complete date of birth the registrar may enter the year of birth only. This could be an approximation if the informant is not sure of the year of birth.
In order to try to quantify the error rate in age at death in the death statistics of those dying at the oldest ages, we would ideally validate the date of birth supplied to registrars in England and Wales by matching to the birth record or certificate of the deceased. We do validate the age of all supercentenarians (those aged 110 and over) dying in England and Wales but the numbers are too small (around 10 a year) to draw any meaningful conclusions.
In 2014, there were 103,420 deaths registrations in England and Wales of people aged 90 and over. It would be prohibitively expensive to validate all of these by matching death and birth certificates. The ESRC Centre for Population Change at the University of Southampton has funded the validation of a sample of deaths of semi-supercentenarians (those aged 105 to 109) who were born in England and Wales. This work has been completed for both males and females and the results are presented below.
Validation results for supercentenarian and semi-supercentenarian deaths registered in England and Wales6
Validation of male deaths registered in England and Wales aged 105 and over
According to the death statistics, 365 male deaths were registered in England and Wales aged 105 to 109 between the years 2000 and 2014, with a further 10 deaths of males aged 110 or over. From the data recorded on the death certificate, 50 of the cases aged 105 to 109 were either born outside England and Wales or no place of birth was recorded. These cases were excluded from the validation exercise as it is difficult to obtain birth records for these individuals. The remaining 315 death records (86% of the total) aged 105 to 109 were extracted and validated by the General Register Office (GRO) (that is, matching the date of birth on the death certificate to the deceased’s birth certificate). The deaths of those aged 110 and over (supercentenarians) are currently checked directly by us against birth records obtained from GRO as part of a separate exercise for validating deaths of supercentenarians.
Tables 1a and 1b show the results of the validation exercise by age at death, including the numbers of cases fully, partially and not validated.
Table 1a: Male deaths at ages 105 and over registered in England and Wales, 2000 to 2014
| Age at death | Number registered | Number fully validated* | Number partially validated# | Number Incorrect | Number not validated | Percentage fully validated* | Percentage fully or partially validated |
| 105 | 212 | 186 | 1 | 1 | 24 | 87.7 | 88.2 |
| 106 | 70 | 58 | 2 | 1 | 9 | 82.9 | 85.7 |
| 107 | 45 | 35 | 1 | 0 | 9 | 77.8 | 80.0 |
| 108 | 29 | 22 | 0 | 0 | 7 | 75.9 | 75.9 |
| 109 | 9 | 2 | 1 | 0 | 6 | 22.2 | 33.3 |
| 110+ | 10 | 5 | 0 | 0 | 5 | 50.0 | 50.0 |
| Total | 375 | 308 | 5 | 2 | 60 | 82.1 | 83.5 |
| Source: Office for National Statistics | |||||||
| Notes: | |||||||
| 1. * Fully validated cases are those where a birth record was found which matched the same date and place of birth and the same full name (and aliases). # Partially validated cases are those which appear to have a transcription error which does not invalidate the age at death. | |||||||
Download this table Table 1a: Male deaths at ages 105 and over registered in England and Wales, 2000 to 2014
.xls (19.5 kB)
Table 1b: Male deaths at ages 105 and over registered in England and Wales who were born in England and Wales, 2000 to 2014
| Age at death | Number registered | Number fully validated* | Number partially validated# | Number incorrect | Number not validated | Percentage fully validated* | Percentage fully or partially validated |
| 105 | 190 | 186 | 1 | 1 | 2 | 97.9 | 98.4 |
| 106 | 63 | 58 | 2 | 1 | 2 | 92.1 | 95.2 |
| 107 | 36 | 35 | 1 | 0 | 0 | 97.2 | 100 |
| 108 | 23 | 22 | 0 | 0 | 1 | 95.7 | 95.7 |
| 109 | 3 | 2 | 1 | 0 | 0 | 66.7 | 100 |
| 110+ | 5 | 5 | 0 | 0 | 0 | 100 | 100 |
| Total | 320 | 308 | 5 | 2 | 5 | 96.3 | 97.8 |
| Source: Office for National Statistics | |||||||
| Notes: | |||||||
| 1. * Fully validated cases are those where a birth record was found which matched the same date and place of birth and the same full name (and aliases). # Partially validated cases are those which appear to have a transcription error which does not invalidate the age at death. | |||||||
Download this table Table 1b: Male deaths at ages 105 and over registered in England and Wales who were born in England and Wales, 2000 to 2014
.xls (20.0 kB)For the 320 deaths recorded as being born in England and Wales, 308 cases were fully validated. There were an additional 5 cases where it is likely that there was an incorrectly recorded date of birth. In all these cases this related to an incorrect day being recorded (with the month and year being correct); these are likely to be transcription errors. There were 5 cases where a matching birth record could not be found, 1 case where the recorded age at death appeared to be wrong (and less than 105) and 1 case where the person appeared to be female, rather than male. These are all included in the numbers of registered deaths.
Overall, there was a very high validation rate of over 96% for deaths aged 105 and over registered in England and Wales where the person was born in England and Wales. This rises to 98% if those cases with a transcription error resulting in a different date of birth by a few days are also included as validated. However, nearly 15% of deaths registered during 2000 to 2014 in England and Wales, or people aged 105 and over, were of males born outside England and Wales, for most of whom it is not possible to validate the date of birth and hence the derived age at death. This does not mean that the age at death is incorrect in these cases but it does give an indication of the potential number of cases where the age at death cannot be verified and hence may be incorrect.
Validation of female deaths registered in England and Wales aged 105 and over
According to the death statistics, 3,559 female deaths were registered in England and Wales aged 105 to 109 between the years 2000 and 2014. Of these, 274 cases were either born outside England and Wales or no place of birth was recorded, leaving 3,285 cases (92% of the total) born in England and Wales. A stratified sample5 of these deaths was selected yielding 739 death records which were extracted and sent to GRO for validation. There were a further 93 deaths of females aged 110 and over during 2000 to 2014; of these, 82 were born in England and Wales or Scotland and the deaths of these supercentenarians were validated directly by us, as for males. Table 2a shows the total numbers of female deaths registered during 2000 to 2014 and those born in England and Wales by age and the numbers in each age group selected for the samples. All the deaths aged 109 and over were subject to validation.
Table 2a: Female deaths at age 105 and over registered in England and Wales, 2000 to 2014
| Age at death | Number registered | Number born in E and W | Sample size for validation | Sample size as percentage of total deaths born in E and W |
| 105 | 1775 | 1645 | 162 | 9.8 |
| 106 | 907 | 837 | 124 | 14.8 |
| 107 | 475 | 437 | 155 | 35.5 |
| 108 | 264 | 238 | 170 | 71.4 |
| 109 | 138 | 128 | 128 | 100 |
| 110+ | 93 | 82 | 82 | 100 |
| Total | 3652 | 3367 | 821 | 24.4 |
| Source: Office for National Statistics | ||||
| Notes: | ||||
| 1. * Fully validated cases are those where a birth record was found which matched the same date and place of birth and the same full name (and aliases). # Partially validated cases are those which appear to have a transcription error which does not invalidate the age at death. | ||||
Download this table Table 2a: Female deaths at age 105 and over registered in England and Wales, 2000 to 2014
.xls (19.5 kB)
Table 2b: Female deaths at age 105 and over registered in England and Wales, 2000 to 2014: Sample selected for validation
| Age at death | Number registered | Number fully validated* | Number partially validated# | Number possibly correct | Incorrect age | Number not validated | Percentage fully validated* | Percentage partially validated |
| 105 | 162 | 154 | 1 | 3 | 0 | 4 | 95.1 | 95.7 |
| 106 | 124 | 121 | 1 | 2 | 0 | 0 | 97.6 | 98.4 |
| 107 | 155 | 149 | 0 | 0 | 0 | 6 | 96.1 | 96.1 |
| 108 | 170 | 159 | 2 | 1 | 2 | 6 | 93.5 | 94.7 |
| 109 | 128 | 124 | 3 | 0 | 0 | 1 | 96.9 | 99.2 |
| 110+ | 82 | 80 | 1 | 0 | 0 | 1 | 97.6 | 98.8 |
| Total | 821 | 787 | 8 | 6 | 2 | 18 | 95.9 | 96.8 |
| Source: Office for National Statistics | ||||||||
| Notes: | ||||||||
| 1. * Fully validated cases are those where a birth record was found which matched the same date and place of birth and the same full name (and aliases). # Partially validated cases are those which appear to have a transcription error which does not invalidate the age at death. | ||||||||
Download this table Table 2b: Female deaths at age 105 and over registered in England and Wales, 2000 to 2014: Sample selected for validation
.xls (20.0 kB)For the 821 deaths in the sample recorded as being born in England and Wales, 787 cases were fully validated. There were an additional 8 cases where it is likely that there was an incorrectly recorded date of birth. In all cases this related to an incorrect day being recorded (with the month and year being correct); these are likely to be transcription errors. There were a further 2 cases where the year of birth recorded appeared to be incorrect (but the people involved were still supercentenarians at death). These are shown as incorrect ages in Table 2b. There were 18 cases where a matching birth record could not be found and 6 cases which were possible matches but where the surname or maiden name didn’t match between the birth and death certificates. These are all included in the numbers of registered deaths in Table 2b.
Overall, there is a very high validation rate of over 96% for deaths aged 105 and over registered in England and Wales where the person was born in England and Wales. This rises to 97% if those cases with a transcription error resulting in a different date of birth by a few days are also included as validated. However, around 7.8% of female deaths aged 105 and over were in respect of females born outside of England and Wales, for most of whom it is not possible to validate the date of birth and hence the derived age at death.
For the cases where age validation is possible, there is some misreporting of date of birth on death registrations. However, for cases where full or partial validation could be made there were only 3 cases where the data on the birth certificate was sufficiently different from that recorded on the death certificate as to give a different age at death than that calculated. There were a further 13 cases where there appeared to be a small transcription error but which did not invalidate the age at death calculated. This would suggest that there are very few errors in the recorded age at death, at least for those born in England and Wales. It is not possible to state whether this is also the case for those born outside of England and Wales.
Age validation of all male and female supposed super- and semi-supercentenarians males who died between 2000 and 2014 indicated a minimum 1% to 2% error in the date of birth recorded on these death records, albeit a large proportion of these errors were minor and did not invalidate the age at death.
The evidence from those aged 105 and over suggests that there is a high degree of accuracy in age at death on death certificates for those born in England and Wales. We have not tested whether this level of accuracy holds for those aged 90 to 104. However, we are currently in the process of extending the age validation work to a sample of death records of those dying aged 90 to 94. As the majority of the age 90 and over population are aged below 95, this combined with the results of the sample of deaths of those dying aged 105 and over will give us a good indication of the level of accuracy for the whole of the 90 and over age group.
The level of error for those dying at ages 80 and over who were born outside of England and Wales is unknown. In 2014, approximately 10% of people who died in England and Wales aged 90 and over were born outside of England and Wales (7% were born outside of the UK, the remaining 3% were born in the rest of the UK or the Channel Islands). This could impact on the accuracy of age at death data at high ages.
Completeness of death data
It is a legal requirement for all deaths occurring in England and Wales to be registered. Death registration data is therefore taken to be complete.
Deaths of visitors and residents of other UK countries that occurred in England and Wales are included in the total death figures for England and Wales (but not in the sub-national geographical breakdowns). In 2014, 0.22% (1,110) of all deaths registered were of residents from outside England and Wales. Deaths of residents of England and Wales that occur and are registered outside of England and Wales are not included. An assumption is made that these cancel each other out.
Death registrations and death occurrences
We publish deaths data on a registration basis, that is, deaths are allocated to the year in which they were registered. However, between 1993 and 2005 data were published on an occurrence basis, that is, the number of deaths that occurred in the reference period.
Although the majority of mortality publications are now based on registrations, we continue to take an annual extract of death occurrences in the autumn (early to mid-September) following the data year. Deaths that occurred before that date but that have not yet been registered will not be included.
Death occurrence data is used for seasonal analysis of mortality data and as input data for the calculation of population estimates.
There is evidence of increasing delays in the registering of deaths. Between 2007 and 2013 there have been around 3,000 records per year which have not been included in the annual death occurrence dataset for each year because they were registered after the date the extract was taken. This is higher than in previous years. The number of late registrations by year of occurrence for the latest years shown in Table 3 are likely to be subject to future revisions due to the addition of further late registrations. The figure for 2014 is currently around 2,500. (These figures are as at November 2016.)
Table 3: Number of late registrations not included in the annual death occurrence dataset, England and Wales, 2000 to 2014
| All deaths | Deaths aged 80 and over | |||||
| Year death occurred | Number of deaths in occurrence dataset | Number of late death registrations not included | % late | Number of deaths in occurrence dataset | Number of late death registrations not included | % late |
| 2001 | 530,373 | 1,377 | 0.26 | 257,815 | 153 | 0.06 |
| 2002 | 533,527 | 1,759 | 0.33 | 265,400 | 186 | 0.07 |
| 2003 | 538,254 | 2,036 | 0.38 | 273,472 | 214 | 0.08 |
| 2004 | 512,541 | 2,252 | 0.44 | 260,466 | 270 | 0.1 |
| 2005 | 512,692 | 2,431 | 0.47 | 264,915 | 307 | 0.12 |
| 2006 | 502,633 | 1,727 | 0.34 | 260,399 | 200 | 0.08 |
| 2007 | 502,484 | 3,479 | 0.69 | 264,972 | 521 | 0.2 |
| 2008 | 505,639 | 3,473 | 0.69 | 270,277 | 565 | 0.21 |
| 2009 | 487,279 | 3,314 | 0.68 | 260,168 | 551 | 0.21 |
| 2010 | 491,449 | 3,043 | 0.62 | 265,648 | 512 | 0.19 |
| 2011 | 481,156 | 3,118 | 0.65 | 261,942 | 539 | 0.21 |
| 2012 | 499,240 | 3,814 | 0.76 | 278,425 | 727 | 0.26 |
| 2013 | 502,670 | 2,887 | 0.57 | 281,099 | 541 | 0.19 |
| 2014 | 499,770 | 2,507 | 0.5 | 278,630 | 457 | 0.16 |
| Source: Office for National Statistics (Data extracted November 2016) | ||||||
| Notes: | ||||||
| 1. Figures are taken from a live system so may not match figures in publications taken at a set point in time. Data extracted November 2016 | ||||||
Download this table Table 3: Number of late registrations not included in the annual death occurrence dataset, England and Wales, 2000 to 2014
.xls (20.5 kB)The KT method used to produce population estimates of those aged 90 and over by single year of age requires deaths data for those dying from the age of 80.
Table 3 above shows late registrations not included in the annual death occurrences as a percentage of the occurrence deaths for all deaths and for those aged 80 and above; the percentage is lower for those aged 80 and over than for the all age group.
The advantage of using the annual deaths occurrence dataset to produce population estimates is that all deaths are assigned to the year in which they occurred (accuracy). The disadvantage is that late death registrations may not be included in the occurrence dataset (completeness).
The advantage of using death registration data is that historically all deaths are captured (completeness). The disadvantage is that some deaths registered in a particular year will have occurred in previous years (accuracy). The percentage of death registrations that occurred in previous years has increased over the last decade (Tables 4 and 5) both for all ages and for deaths aged 80 and over. However, the percentages are lower for deaths aged 80 and over compared to those for all deaths.
Table 4: Annual dataset year for death registrations (all ages), England and Wales, 2000 to 2014
| Annual Dataset Year for registrations | Number of death registrations | Number registered which occurred in that year | Percentage of those registered that occurred in that year | Number registered which occurred in previous years | Percentage of those registered that occurred in previous years |
| 2001 | 532,498 | 517,010 | 97.1 | 15,488 | 2.9 |
| 2002 | 535,356 | 520,849 | 97.3 | 14,507 | 2.7 |
| 2003 | 539,151 | 524,827 | 97.3 | 14,324 | 2.7 |
| 2004 | 514,250 | 499,081 | 97.1 | 15,169 | 2.9 |
| 2005 | 512,993 | 497,603 | 97 | 15,390 | 3 |
| 2006 | 502,599 | 485,202 | 96.5 | 17,398 | 3.5 |
| 2007 | 504,052 | 485,068 | 96.2 | 18,984 | 3.8 |
| 2008 | 509,090 | 488,764 | 96 | 20,326 | 4 |
| 2009 | 491,348 | 471,113 | 95.9 | 20,235 | 4.1 |
| 2010 | 493,242 | 473,661 | 96 | 19,581 | 4 |
| 2011 | 484,367 | 463,450 | 95.7 | 20,917 | 4.3 |
| 2012 | 499,331 | 478,733 | 95.9 | 20,598 | 4.1 |
| 2013 | 506,790 | 482,658 | 95.2 | 24,132 | 4.8 |
| 2014 | 501,424 | 477,752 | 95.3 | 23,672 | 4.7 |
| Source: Office for National Statistics | |||||
Download this table Table 4: Annual dataset year for death registrations (all ages), England and Wales, 2000 to 2014
.xls (27.6 kB)Of the 501,424 deaths registered in 2014, 477,752 occurred in 2014, 21,474 occurred in 2013, 1,655 occurred in 2012 and 543 occurred prior to 2012.
Table 5: Annual dataset year for death registrations (ages 80 and over), England and Wales, 2000 to 2014
| Annual Dataset Year for registrations | Number of death registrations | Number registered which occurred in that year | Percentage of those registered that occurred in that year | Number registered which occurred in previous years | Percentage of those registered that occurred in previous years |
| 2001 | 258,346 | 253,911 | 98.3 | 4,435 | 1.7 |
| 2002 | 265,830 | 261,796 | 98.5 | 4,034 | 1.5 |
| 2003 | 273,531 | 269,757 | 98.6 | 3,774 | 1.4 |
| 2004 | 260,579 | 256,673 | 98.5 | 3,906 | 1.5 |
| 2005 | 264,294 | 260,289 | 98.5 | 4,005 | 1.5 |
| 2006 | 259,901 | 254,987 | 98.1 | 4,914 | 1.9 |
| 2007 | 264,948 | 259,345 | 97.9 | 5,603 | 2.1 |
| 2008 | 270,745 | 264,701 | 97.8 | 6,044 | 2.2 |
| 2009 | 261,136 | 255,038 | 97.7 | 6,098 | 2.3 |
| 2010 | 265,331 | 259,654 | 97.9 | 5,677 | 2.1 |
| 2011 | 262,290 | 255,767 | 97.5 | 6,523 | 2.5 |
| 2012 | 277,290 | 270,640 | 97.6 | 6,650 | 2.4 |
| 2013 | 282,515 | 274,075 | 97 | 8,440 | 3 |
| 2014 | 277,315 | 269,621 | 97.2 | 7,694 | 2.8 |
| Source: Office for National Statistics | |||||
Download this table Table 5: Annual dataset year for death registrations (ages 80 and over), England and Wales, 2000 to 2014
.xls (19.5 kB)Figures 1 and 2 show that, for both males and females, there is very little difference in the annual numbers of death occurrences and death registrations and distributions at the oldest ages with year-on-year losses and gains broadly cancelling each other out; for example, 2010 death registrations won’t include deaths that occurred in 2010 but were registered after the end of the year and will include deaths that occurred in previous years but were not registered until 2010. 2010 death occurrences won’t include deaths that occurred in 2010 but were not registered until later.
The difference in the number of deaths occurring and the number registered in a year is influenced by the number of deaths going to inquest which can delay registration. Also, the pattern of public holidays at the end of a year may mean that some deaths occurring at the end of one year cannot be registered until the first working day in the following year.
Figure 1: Death occurrences as a percentage of death registrations, Males, 1993 to 2014
England and Wales
Source: Office for National Statistics
Download this chart Figure 1: Death occurrences as a percentage of death registrations, Males, 1993 to 2014
Image .csv .xls
Figure 2: Death occurrences as a percentage of death registrations, females, 1993 to 2014
England and Wales
Source: Office for National Statistics
Download this chart Figure 2: Death occurrences as a percentage of death registrations, females, 1993 to 2014
Image .csv .xls
Table 6: Number of death registrations and death occurrences at age 80 and over by age group, 2014
| Males | Females | |||
| Occurrences | Registrations | Occurrences | Registrations | |
| 80-89 | 82,100 | 81,957 | 92,301 | 91,938 |
| 90-99 | 31,990 | 31,779 | 66,590 | 66,079 |
| 100-104 | 840 | 819 | 4,414 | 4,354 |
| 105 & over | 46 | 45 | 349 | 344 |
| total 80+ | 114,976 | 114,600 | 163,654 | 162,715 |
| Source: Office for National Statistics | ||||
Download this table Table 6: Number of death registrations and death occurrences at age 80 and over by age group, 2014
.xls (18.9 kB)Table 6 shows the distributions of death occurrences and death registrations by 80 and over age groups are very similar for both male and female deaths.
The year-on-year numbers and distributions of death registration and death occurrence data at older ages are very similar, meaning the impact of using one in preference to the other is likely to be minimal. However, external researchers using deaths data for England and Wales published by us in their own models should be aware that there is a potential issue with using this data as a time series. Deaths data published for years pre-1993 are death registrations. Death occurrences were published for the years 1993 to 2005 and from 2006 death registrations data have been published6.
Deaths data used in the calculation of official mid-year population estimates
Death occurrences by sex and single year of age for ages 0 to 89 and those aged 90 and over are used in the production of official annual mid-year population estimates (MYEs) published at the end of June each year.
The deaths data extract required for the production of the MYE is usually taken by early December of the reference year. At this time, the reference death occurrence figures will still be provisional. (The final death occurrence dataset for any year is not taken until the autumn of the following year so that as many late death registrations as possible are included in the dataset.) The difference between the previous year’s provisional death occurrences for the January to June period and the finalised figures for that period is then applied to the January to June provisional figures for the reference year to try to mitigate possible under-count.
The data are adjusted so that anyone born in the first half of a calendar year is aged on to the age they would have been at 30 June of the year of death; anyone born in the second half of a calendar year is aged on to the age they would have been at 30 June of the calendar year following.
Deaths data used in the calculation of Kannisto-Thatcher (KT) estimates
Deaths data for those aged 85 and over by single year of age are used to calculate the Estimates of the very old data series using the KT method.
KT estimates are calculated using deaths occurrence data for all years prior to the reference year and registration data for the reference year. (This is because the estimates are produced in August before the annual extract of occurrence data has been taken for the reference year.) The KT estimates are produced at this time so they are ready to feed into the annual life tables that are published in September and the biennial national population projections that are published in October.
Work has been done to compare estimates of the very old produced using death occurrence data and deaths registration data and the current method (using death occurrences for all years prior to the reference year and registration data for the reference year). This results in only small differences in the totals and distributions of the estimates. The choice between using annual deaths registration data and death occurrence data in the production of the KT estimates of the very old is a trade-off between accuracy of year of death (occurrences), completeness of deaths data over time (registrations) and timeliness.
Extracting death occurrences from a live dataset that is updated daily could help to resolve the issue of completeness (any late death registrations coming into the system up to the day death occurrences were extracted would be included in the death occurrence dataset extracted, including deaths occurring in previous years). This would not completely address the issue of completeness as there would still be late registrations that come into the system after the extract is taken. It could also lead to comparability and consistency problems with figures inconsistent between publications; however, it is something we could consider in the future.
Summary and conclusions
Accuracy:
deaths data is of very high quality in terms of accuracy of age at death for those dying at ages 105 and over in England and Wales who were born in England and Wales
validation of age at death for those dying at age 105 and over, born outside of England and Wales, was not possible; we do not know the level of accuracy of age at death for these cases
deaths are assigned to the year in which they occurred in death occurrence datasets but in death registration datasets some deaths registered in a particular year will have occurred in previous years
Completeness:
it is a legal requirement for all deaths occurring in England and Wales to be registered so these deaths data can be taken as complete
death occurrence data excludes deaths that were registered after the extraction of the annual occurrence dataset
the year-on-year numbers and distributions of death registration and death occurrence data at older ages are very similar, meaning the impact of using one in preference to the other for the production of KT estimates is minimal
Next steps
investigate the possibility of producing population estimates from death occurrences extracted from the live database to help increase completeness
extend the validation of deaths to a sample of all those aged 90 and over
although complete validation of deaths for people born outside of England and Wales is not possible, consider ways of partially validating these deaths, for example by examining the consistency of recorded date of birth over time for the subset of these records that appear on the ONS Longitudinal Study.
Notes for A1. Deaths data
- 19% of all deaths in England and Wales in 2014 and 12% of deaths of those dying at age 80 and over were certified by a coroner.
- Guidance notes for doctors completing MCCDs
- More details on quality checks carried out on deaths data are described in the User Guide to Mortality Statistics.
- Also published as a CPC Technical Paper
- Funding had been agreed for the validation of 800 female records. The sample was designed to provide a minimum of 100 records for each single year of age. After extracting cases where births had occurred outside of England and Wales, for each year of age every nth record was select to achieve this; for example, for age 105 every tenth record was selected; for age 109, as there were only 128 records in total, all of these were selected.
- Death registration data by single year of age for 1963 to 2015 for England and Wales has been published.
6. A2. Quality of Census data at older ages
Introduction
The decennial census in England and Wales provides benchmark estimates of the population by age and sex. They are used as the basis for the inter-censal mid-year estimates (MYEs) and every 10 years as a means of rebasing the population estimates. The MYEs are produced by rolling forward the census population estimates allowing for ageing, births, deaths and net migration (the cohort component method). Any error in the age 90 and over census estimate is thereby carried forward to the inter-censal MYE and will be reflected in the estimates of the very old, as these are constrained to the MYE 90 and over totals.
The 2011 MYE of those aged 90 and over in England and Wales based on the 2011 Census estimate was 440,300. This was 31,400 fewer people aged 90 and over than had been estimated for mid-2011 by rolling forward the data from the 2001 Census. As a result, the MYEs for those aged 90 and over for the period 2002 to 2010 were revised downwards by 7% by the end of the decade. The 2001 MYEs (based on the 2001 Census) were assumed to be correct. This means that any error (over-count) in high-age estimates in the 2001 Census would not have been corrected and the estimates may still be too high in the 2001 to 2010 inter-censal year MYEs.
Research reported in this section builds on previous research we have published on the quality of the 2011 Census estimates1.
As the 2011-based MYEs are rolled forward, any overestimation at high ages is likely to progressively increase as the size of the cohort reduces (as any overestimate in the population would not be removed by deaths). The effect will be greater for men than women as there are smaller cohorts of men at older ages than women.
Quality of the 2011 Census estimates of the 80 and over population
It is important to note that census estimates include some level of imputation and are therefore not simply counts of people. Census estimates are higher than the census count because they include an estimate of the impact of over and under coverage of the population (such as residents who were counted more than once, or residents who were missed). This coverage adjustment is based mainly on the results of the Census Coverage Survey (CCS) that we conduct. The level of error in the census estimates is dependent on a combination of the size of the population, the census response rate, the CCS sample size the CCS response rate and the homogeneity of the population being estimated.
Confidence intervals are indicators of the extent to which the estimate may differ from the true population value (a 95% confidence interval can be interpreted as the interval within which 95 times out of 100 the true value will lie if the sample were repeated many times).
At an England and Wales level, the 2011 Census estimate for the population as a whole had a 95% confidence interval of plus or minus 0.148%.
At the England and Wales level, the census estimates for both males and females aged 80 and over had a 95% confidence interval of plus or minus 0.33%2. This means at the 95% confidence level the true population value of males aged 80 and over fell between 959,926 plus or minus 3,168 and for females fell between 1,632,767 plus or minus 5,388.
Previous validation of date of birth in census records for the oldest old
In addition to non-response there are a number of other possible sources of error in the census estimate of the high-age population. Age of a respondent is derived from the difference between the date of birth reported and recorded in the census and the date of the census. Potential sources of error include misreporting of date of birth by either the respondent or by proxy completer and mis-recording of date of birth due to processing or scanning errors. Such inaccuracies have been documented in previous censuses.
1971 Census: 3The date of birth of a sample of supposed centenarians in the 1971 Census were checked against the date of birth held for these people in the National Health Service Central Register (NHSCR). It was found that some people had given dates of birth in the census earlier than the dates as shown by their birth registrations. In many cases the error was exactly 20 or 30 years.
1981 Census: 4Out of the 3,727 supposed centenarians in the census only 1,644 were successfully traced in the NHSCR and found to have a matching age. Again there were many cases in which the census age differed from the NHSCR age by a round number like 10, 20 or 30 years, suggesting processing errors.
1991 Census: 5There were no checks on centenarian ages in the 1991 Census. The figure of 6,600 centenarians was published without any mention of errors that had been discovered in the previous censuses. However, there was a later appraisal of the 1991 estimate by the Population Statistics Division of OPCS and Government Actuary’s Department (GAD) and the census figure was rejected in favour of an estimate of 4,400. This was a figure derived from death registrations.
2001 Census: 6Research carried out by our Population Statistics Division in 2008 based on a sample of those aged 90 and over in the Office for National Statistics (ONS) Longitudinal Study (ONS-LS) found the 2001 Census count for males aged 90 and over was 15% higher than the count based on the ONS-LS sample and 8% higher for females.
Results to date from the current investigation into the accuracy of the 2011 Census estimate of those aged 80 and over are reported below. This research has also been conducted using the7 ONS-LS.
The ONS-LS links census and life event information for a 1.1% sample of the population of England and Wales. The original sample was selected from the 1971 Census and incorporated data on individuals born on 1 of 4 selected dates of birth. The sample has been updated at each successive census by taking individuals with the same 4 dates of birth in each year and linking them to existing data. Life event information of individuals with the 4 dates of birth has also been linked. Data linked are births, death, cancer registrations and immigration, and emigration events. The ONS-LS sample excludes imputed census cases. It is also corrected for multiple enumerations.
Analysis
In order to assess the quality of year of birth information for the oldest old in the 2011 Census records, all those in the ONS-LS sample aged 80 and over and usually resident at the time of the 2011 Census were selected (27,330 cases)8. Age in years was calculated from the difference between the date of birth recorded for each case and the date of the 2011 Census.
The longitudinal nature of the ONS-LS means that it was possible to check the consistency of year of birth recorded for the selected sample across all available previous censuses (1971, 1981, 1991 and 2001). Year of birth recorded at the 2011 Census was also compared with year of birth recorded in the latest available information on NHS Digital’s MIDAS9,10, system and any available linked cancer and embarkation records. 23 cases could not be traced on MIDAS. These cases were excluded from the analysis, resulting in a sample of 27,307 ONS-LS members aged 80 and over at the time of the 2011 Census.
Table 7: Office for National Statistics Longitudinal Study (ONS-LS) sample aged 80 and over at 2011 Census
| 2011 Census age | Male | Female | Total | % |
| 80-84 | 6,017 | 8,222 | 14,239 | 52.1 |
| 85-89 | 3,074 | 5,572 | 8,646 | 31.7 |
| 90-94 | 1,020 | 2,446 | 3,466 | 12.7 |
| 95-99 | 169 | 673 | 842 | 3.1 |
| 100+ | 17 | 97 | 114 | 0.4 |
| Total | 10,297 | 17,010 | 27,307 | 100 |
| Source: Office for National Statistics - Longitudinal Study | ||||
Download this table Table 7: Office for National Statistics Longitudinal Study (ONS-LS) sample aged 80 and over at 2011 Census
.xls (18.4 kB)84% of the sample were aged 80 to 89 and almost two-thirds (62.3%) were female. Of the sample, 4,422 (16%) were aged 90 and over (Table 7).
Records available for analysis
Of the sample, 21,851 (80%) had been present at all 5 censuses for which records are available; 3,350 (12%) had been present at 4 of the available censuses in total; 779 (3%) had been present at 3 censuses; 386 (1%) had been present at 2 censuses and there were 941 cases (3%) that had no previous census record before the 2011 Census (Table 8).
Table 8: Number of censuses present at, 1971 to 2011 Censuses
| Number of censuses | Number | Percent | Cumulative Percent |
| 1 | 941 | 3.4 | 3.4 |
| 2 | 386 | 1.4 | 4.9 |
| 3 | 779 | 2.9 | 7.7 |
| 4 | 3,350 | 12.3 | 20.0 |
| 5 | 21,851 | 80.0 | 100.0 |
| Total | 27,307 | 100.0 | |
| Source: Office for National Statistics - Longitudinal Study | |||
Download this table Table 8: Number of censuses present at, 1971 to 2011 Censuses
.xls (26.6 kB)In total, 26,366 cases had records for at least 2 of the 5 available censuses. Of these 24,753, 94% had a consistent year of birth recorded for all censuses they were present at and 1,613 cases had at least 1 discrepant year of birth across their census records (Table 9).
Table 9: Number of censuses present at by number of unique year of birth values recorded across 1971 to 2011 Censuses
| Number of unique year of birth values across all census records | ||||||
| 1 | 2 | 3 | 4 | Total | ||
| Number of censuses present at | 1 | 941 | N/A | N/A | N/A | 941 |
| 2 | 355 | 31 | N/A | N/A | 386 | |
| 3 | 699 | 76 | 4 | N/A | 779 | |
| 4 | 3105 | 233 | 12 | 0 | 3350 | |
| 5 | 20594 | 1183 | 62 | 12 | 21851 | |
| Total | 25694 | 1523 | 78 | 12 | 27307 | |
| Source: Office for National Statistics - Longitudinal Study | ||||||
Download this table Table 9: Number of censuses present at by number of unique year of birth values recorded across 1971 to 2011 Censuses
.xls (18.9 kB)All of the 27,307 cases in the sample had a year of birth recorded on their MIDAS record. 31% (8,423 cases) also had a cancer record that included year of birth but only 334 cases had an embarkation record.
These non-Census records were examined for the 941 cases that had no previous census record before the 2011 Census. The most likely explanation for why these cases only appear for the first time in the 2011 Census is that the respondent (or a proxy respondent) has erroneously entered a date of birth that is one of the 4 designated ONS-LS birthdays11.
For 878 of the 941 cases, the other available record(s) of year of birth was the same as the 2011 Census record so in total 25,631 cases out of the 27,307 (93.9%) had a year of birth in their census records that was consistent with their previous census records or, where the 2011 Census was their only census record, with their other available records.
Of the remaining 63 records, 61 had only 1 other record of year of birth (on their MIDAS record) and that was different to the year of birth recorded at the 2011 Census.
25 out of the 61 cases were aged 80 and over according to both their 2011 Census record and their MIDAS record. However, 36 cases had a recorded MIDAS age of below 80 (Table 10).
Table 10: Age on MIDAS record by 2011 Census age
| 2011 Census age | |||||||
| 80-84 | 85-89 | 90-94 | 95-99 | 100+ | Total | ||
| MIDAS age | Under 35 | 7 | 1 | 3 | 1 | 1 | 13 |
| 35-49 | 0 | 3 | 2 | 1 | 2 | 8 | |
| 50-69 | 2 | 1 | 0 | 0 | 1 | 4 | |
| 70-79 | 7 | 2 | 1 | 1 | 0 | 11 | |
| 80-84 | 3 | 2 | 1 | 0 | 0 | 6 | |
| 85-89 | 5 | 5 | 0 | 0 | 1 | 11 | |
| 90-94 | 0 | 1 | 3 | 3 | 0 | 7 | |
| 95-99 | 0 | 1 | 0 | 0 | 0 | 1 | |
| Total | 24 | 16 | 10 | 6 | 5 | 61 | |
| Source: Office for National Statiistics - Longitudinal Study | |||||||
Download this table Table 10: Age on MIDAS record by 2011 Census age
.xls (18.9 kB)The 2 other cases also had a cancer record. For 1 of these cases their 2011 Census year of birth matched the year of birth on their cancer record but the year of birth on their MIDAS record differed; in the other case the year of birth on their cancer and MIDAS records matched but differed from their recorded 2011 Census year of birth.
The next stage of the analysis examined discrepancies in year of birth across all available records for sample members. (All records were included in the analysis as it would be possible, for example, for a sample member to have been present at 3 censuses with a consistent year of birth recorded but also to have a MIDAS record, a cancer record and an embarkation record that also had a consistent but different recorded year of birth).
All sample members had at least 2 records available, a 2011 Census record (by definition), and a MIDAS record. The maximum number of records a sample member could have was 8: a census record for all 5 censuses 1971 to 2011, a MIDAS record, a 12cancer record and an embarkation record.
Table 11: Number of available records of year of birth
| Number | Percent | Cumulative Percent | ||
| Number of records | 2 | 851 | 3.1 | 3.1 |
| 3 | 364 | 1.3 | 4.4 | |
| 4 | 644 | 2.4 | 6.8 | |
| 5 | 2469 | 9 | 15.8 | |
| 6 | 15834 | 58 | 73.8 | |
| 7 | 7110 | 26 | 99.9 | |
| 8 | 35 | 0.1 | 100 | |
| Total | 27307 | 100 | ||
| Source: Office for National Statistics - Longitudinal Study | ||||
Download this table Table 11: Number of available records of year of birth
.xls (18.4 kB)Of the 27,307 cases in the sample, 84% had 6 or more records available for analysis (Table 11).
Looking across all the available records for 25,526 cases (93.5%) there were no year of birth discrepancies.
1,781 cases (6.5%) had at least 1 discrepant year of birth across all their records. Of these, 1,680 cases had 2 unique years of birth recorded, 86 cases had 3 unique years of birth recorded and 15 cases had 4 unique years of birth recorded.
Table 12: Cases with at least 1 discrepant year of birth as a percentage of sample cases by 2011 Census age
| Number of cases with at least one discrepant record | Number in sample | Percent (of cases with at least one discrepant record) | ||
| 2011 Census age | 80-84 | 827 | 14,239 | 5.8 |
| 85-89 | 586 | 8,646 | 6.8 | |
| 90-94 | 241 | 3,466 | 6.9 | |
| 95-99 | 106 | 842 | 12.6 | |
| 100+ | 21 | 114 | 18.4 | |
| Total | 1,781 | 27,307 | 6.5 | |
| Source: Office for National Statistics - Longitudinal Study | ||||
Download this table Table 12: Cases with at least 1 discrepant year of birth as a percentage of sample cases by 2011 Census age
.xls (18.9 kB)The percentage of records with a discrepant year of birth increases with age of the census respondent. (The number of records per respondent did not vary significantly by 80 and over age groups.) Although the rate of discrepant records was 6.5% for the sample overall, for those aged 95 and over the percentage of discrepant records rises to 13.3%, suggesting the reliability of year of birth data decreases with age (Table 12).
Probable “true” year of birth
In the following analysis, for those cases with no year of birth discrepancies across all of their records, the single year of birth recorded was assumed to be the true value.
For the 1,781 cases with at least 1 discrepancy in their year of birth records, the modal (most commonly recorded) year of birth was designated the ”true” year of birth.
The following rules were applied for cases where there was more than 1 modal year of birth.
Where a case had the same number of unique values as records, the mode was designated as not applicable. There were 61 cases in total where this was the case. (These are the cases reported above that appear in census records for the first time in the 2011 Census.)
All other possible multi-modal cases were examined as detailed in Table 13.
Table 13: Year of birth multi-modal combinations and incidences
| Number records of year of birth available | Possible bi-modal combinations | Possible tri-modal combinations | Possible quad-modal combinations |
| 4 | 2,2 (6 cases) | ||
| 5 | 2,2,1 (3 cases) | ||
| 6 | 2,2,1,1 (2 cases) | 2,2,2 (1 case) | |
| 3,3 (21 cases) | |||
| 7 | 2,2,1,1,1 (0 cases) | 2,2,2,1 (0 cases) | |
| 3,3,1 (3 cases) | |||
| 8 | 2,2,1,1,1,1 (0 cases) | 2,2,2,1,1 (0 cases) | 2,2,2,2 (0 cases) |
| 3,3,1,1 (0 cases) | |||
| 4,4 (0 cases) | |||
| Source: Office for National Statistics - Longitudinal Study | |||
Download this table Table 13: Year of birth multi-modal combinations and incidences
.xls (27.6 kB)There were 36 multi-modal cases in total (Table 13). For these cases the decision was made to designate the 2011 Census year of birth as the mode (probable true year of birth). This means the results are biased slightly in favour of the 2011 Census records being accurate and any inaccuracies identified are therefore a lower bound. (There was 1 case where the 2011 census year of birth was not one of the multi-modes. The mode for this case was designated as not applicable).
The probability of the mode being the “true” year of birth was then calculated for each case by dividing the frequency of the occurrence of the mode in the available records by the number of records.
How accurate is the recorded 2011 Census year of birth?
For 26,945 cases (98.7% of the sample), the year of birth recorded in the 2011 Census was the modal year of birth across all available records and in 94.7% of these cases the modal year of birth was the only year of birth recorded across all available records. Overall for 99.7% of cases where the 2011 Census year of birth was the same as the modal year of birth, the probability of the mode being the ”true” value was calculated as 0.7 or above (Table 14).
Table 14: Probability that 2011 Census year of birth record is "true" where 2011 Census year of birth is the mode
| Number | Percent | Cumulative Percent | ||
| Probability | Certain | 25,526 | 94.7 | 95 |
| 0.7-0.9 | 1,337 | 5.0 | 100 | |
| 0.5-0.6 | 73 | 0.3 | 100 | |
| less than 0.4 | 9 | - | 100 | |
| Total | 26,945 | 100 | ||
| Source: Office for National Statistics - Longitudinal Study | ||||
Download this table Table 14: Probability that 2011 Census year of birth record is "true" where 2011 Census year of birth is the mode
.xls (27.1 kB)In 300 cases, the 2011 Census year of birth was not the modal year of birth, 1.1% of the total sample. The percentage of cases where the 2011 Census year of birth is not the mode increases by age group (Table 15), reaching 3.3% for those aged 95 to 99 and 7% for those aged 100 and over. For those aged 90 and over as a whole the 2011 Census year of birth was not the mode in 1.9% of cases.
Table 15: 2011 Census age for cases where 2011 Census year of birth is not the modal record
| Number | Percent | Percent of sample age group | ||
| 2011 Census age | 80-84 | 111 | 37 | 0.8 |
| 85-89 | 108 | 36 | 1.2 | |
| 90-94 | 45 | 15 | 1.3 | |
| 95-99 | 28 | 9.3 | 3.3 | |
| 100+ | 8 | 2.7 | 7 | |
| Total | 300 | 100 | 100 | |
| Source: Office for National Statistics - Longitudinal Study |
Download this table Table 15: 2011 Census age for cases where 2011 Census year of birth is not the modal record
.xls (18.9 kB)For 282 (94%) of the 300 cases where the 2011 Census year of birth was not the modal year of birth, the probability of the mode being the true value was calculated as 0.7 or above. (The mode was designated not applicable in 61 cases where there were only 2 available records and the 1 multi-mode case where the 2011 Census year of birth was not one of the modes.)
The accuracy of the 2011 Census recorded year of birth was then compared to the accuracy of year of birth recorded in MIDAS records.
Table 16: Probability that MIDAS year of birth record is "true" where MIDAS year of birth is the mode
| Number | Percent | Cumulative Percent | ||
| Probability | Certain | 25526 | 94 | 94 |
| 0.7-0.9 | 1558 | 5.7 | 99.7 | |
| 0.5-0.6 | 73 | 0.3 | 100 | |
| less than 0.4 | 4 | 0 | 100 | |
| Total | 27161 | 100 | ||
| Source: Office for National Statistics - Longitudinal Study | ||||
Download this table Table 16: Probability that MIDAS year of birth record is "true" where MIDAS year of birth is the mode
.xls (26.6 kB)The degree of accuracy in the MIDAS year of birth records was slightly higher than in the 2011 Census records. For 27,161 cases (99.5% of the sample) the year of birth in the MIDAS records was the modal year of birth across all available records and in 94% of these cases the modal year of birth was the only year of birth recorded across all available records. Overall, for 99.7% of cases where the MIDAS year of birth was the same as the modal year of birth, the probability of the mode being the “true” value was calculated as 0.7 or above (Table 16).
There were only 84 cases where the recorded MIDAS year of birth was not the mode and the proportion of these cases where the probability of the mode being the true year of birth was 0.7 or above was 73%. These figures are lower than the equivalent figures for the 2011 Census year of birth record. (The mode was designated not applicable in 61 cases where there were only 2 available records and the 1 multi-mode case where the 2011 Census year of birth was not one of the modes.)
Nature of the identified discrepancies
Examining the 300 cases where the 2011 Census year of birth is not the modal year of birth, the difference between the 2011 Census year of birth and the mode ranged from 1 year to 80 years with a difference of 1 to 2 years for 39% of these cases and a difference of up to 5 years for 60% of these cases. For 23% of cases the difference was 10 years or more (Table 17). The earlier the 2011 Census recorded year of birth, the more likely it was that the difference was of this magnitude.
Table 17: Difference between the 2011 Census year of birth and the modal year of birth
| Number | Percent | Cumulative Percent | |
| 1 to 2 years | 118 | 39.3 | 39.3 |
| 3 to 5 years | 62 | 20.7 | 60 |
| 6 to 10 years | 52 | 17.3 | 77.3 |
| 10 to 19 years | 12 | 4 | 81.3 |
| 20 years or more | 56 | 18.7 | 100 |
| 300 | 100 | ||
| Source: Office for National Statistics - Longitudinal Study | |||
Download this table Table 17: Difference between the 2011 Census year of birth and the modal year of birth
.xls (18.4 kB)Where the 2011 Census year of birth differed from the mode by only a few years it seems feasible that this is because of misreporting either by a proxy respondent who was unsure of the year of birth of the person for whom they were supplying the information (for example a care home worker) or an elderly person misremembering.
In 287 of the 300 cases (95.7%) where the 2011 Census year of birth was not the modal year of birth, the year of birth on the MIDAS record was the modal year of birth across all available records.
Looking at the discrepancies between the 2011 Census year of birth record and the modal record, a number of other types of misreporting or misrecording were apparent. Examples include young children being put on the census form with a 20th century year of birth as opposed to a 21st, for example, a birth year of 2010 being recorded as 1910 in the 2011 Census. Also reversing of digits, for example, a birth year of 1920 being reported or recorded as 1902 in the 2011 Census.
It is also known that there were some problems when scanning in the 2011 Census forms. The capture of write-in responses using optical character recognition technology is not perfect and is affected by the quality of handwriting. Although high levels of accuracy were achieved in the 2011 Census13, some errors were detected. For example, there was a problem distinguishing 6s and 0s and 7s and 1s14. Looking at the identified discrepancies between the 2011 Census year of birth and the modal year of birth there were a number of examples of this. For example, someone recorded born in 1967 in the modal record being recorded as being born in 1907 in the 2011 Census; or someone born in 1972 in the modal record being recorded as born in 1912 in the 2011 Census record. The numbers of those alive in 2011 born at the beginning of the last century would have been very small compared with the numbers born in the 1960s and 1970s, so this type of scanning error would have a much bigger impact on the census estimate of very old people than younger people.
In 2011, for the first time people had the option of completing the census form online. There was also a problem of 8s and 9s being swapped in some instances with this form of completion. This was evident in the identified discrepancies and probably accounts for a cluster of cases found in the sample of a modal 1919 year of birth but a 2011 Census year of birth of 1918 and vice versa.
For 88 of the 300 cases the modal year of birth was 1932 or later, suggesting that these people were aged below 80.
The modal age and 2011 Census age for all the 300 cases that had a discrepant year of birth are shown in Table 18.
Table 18: Modal age by 2011 Census age (for cases where 2011 Census year of birth was not the mode)
| 2011 Census age | |||||||
| 80 to 84 | 85 to 89 | 90 to 94 | 95 to 99 | 100 and over | Total | ||
| Modal age | Under 35 | 9 | 3 | 3 | 1 | 1 | 17 |
| 35 to 49 | 4 | 6 | 4 | 5 | 1 | 20 | |
| 50 to 69 | 7 | 4 | 2 | 3 | 1 | 17 | |
| 70 to 79 | 21 | 13 | 5 | 2 | 0 | 41 | |
| 80 to 84 | 41 | 33 | 8 | 0 | 2 | 84 | |
| 85 to 89 | 20 | 39 | 6 | 2 | 0 | 67 | |
| 90 to 94 | 9 | 8 | 15 | 13 | 2 | 47 | |
| 95 to 99 | 0 | 2 | 2 | 2 | 1 | 7 | |
| Total | 111 | 108 | 45 | 28 | 8 | 300 | |
| Source: Office for National Statistics - Longitudinal Study | |||||||
Download this table Table 18: Modal age by 2011 Census age (for cases where 2011 Census year of birth was not the mode)
.xls (18.9 kB)For the 300 cases, 95 had a modal age of below 80.
Of the 84 people with a modal age of 80 to 84, 33 had a 2011 Census age of 85 to 89; 8 had a 2011 census age of 90 to 94 and 2 had a 2011 Census age of 100 and over.
Of the 67 people with a modal age of 85 to 89, 20 had a 2011 Census age of 80 to 84; 6 had a 2011 census age of 90 to 94 and 2 had a 2011 Census age of 95 to 99.
Of the 47 people with a modal age of 90 to 94, 9 had a 2011 Census age of 80 to 84; 8 had a 2011 Census age of 85 to 89; 13 had a 2011 Census age of 95 to 99 and 2 had a 2011 Census age of 95 to 99
Of the 7 people with a modal age of 95 to 99, 2 had a 2011 Census age of 85 to 89; 2 had a 2011 census age of 90 to 94 and 1 had a 2011 Census age of 100 and over.
There were some cases in the Office for National Statistics Longitudinal Study (ONS-LS) sample where the 2011 Census recorded age was below 80 but the recorded NHS Digital MIDAS age was 80 or above (90 cases). These cases were also examined.
Of these cases, 69 had at least 2 census records and 49 of these had records for all 5 available censuses. For the remaining 21 cases the 2011 Census record was the only census record and all except 1 had only 1 non-census record, their MIDAS record.
Modal year of birth was not applicable for 17 out of the 90 cases (because the number of unique values for year of birth equalled the number of available records). There was 1 case where there was more than 1 mode. The 2011 Census year of birth was designated as the mode for this case.
In 10 out of the 73 cases where mode was applicable, the 2011 Census year of birth was the modal year of birth and for 8 out of 10 of these cases the probability of the mode being the “true” value was calculated as 0.7 or above.
In 5 cases, the modal year of birth was 1931 and this was also the year of birth recorded in the 2011 MIDAS record. However, the derived age in the 2011 Census records was 79, but in the MIDAS record it was 80.
In total, in 68 out of the 73 cases the MIDAS year of birth was the modal year of birth, 66 of these with a probability that the mode was the ”true” value of 0.7 or above.
Revised ONS-LS sample for those aged 80 and over at the time of the 2011 Census
Table 19 shows the original sample of those aged 80 and over in the ONS-LS according to their 2011 Census records.
Table 19: Original sample
| 2011 Census age | Number |
| 80 to 84 | 14,239 |
| 85 to 89 | 8,646 |
| 90 to 94 | 3,466 |
| 95 to 99 | 842 |
| 100 and over | 114 |
| Total | 27,307 |
| Source: Office for National Statistics - Longitudinal Study | |
Download this table Table 19: Original sample
.xls (17.9 kB)Table 20 shows the sample adjusted by subtracting those cases identified in the previous analysis where the 2011 Census year of birth was not the modal year of birth and the modal year of birth was below age 80 (95 cases). The sample has also been adjusted for those cases where the 2011 Census year of birth was not the modal year of birth and the modal year of birth was 80 and above, but the 2011 Census 80 and above age category differed from the modal 80 and above age category (see Table 18).
Table 20: Intermediate adjusted sample
| 2011 Census age | Number |
| 80-84 | 14,212 |
| 85-89 | 8,605 |
| 90-94 | 3,468 |
| 95-99 | 821 |
| 100+ | 106 |
| Total | 27,212 |
| Source: Office for National Statistics - Longitudinal Study | |
Download this table Table 20: Intermediate adjusted sample
.xls (26.1 kB)In Table 22, further adjustments have been made to the sample by adding in those cases (6115) where 2011 Census age was below 80 but the modal age was age 80 or over and the probability that the mode was correct was 0.7 or above (shown in Table 21 below).
Table 21: Modal age by 2011 Census age: Cases where 2011 Census age is below 80 but mode is 80 and over and probability mode is correct is 0.7 or above
| 2011 Census age | |||||
| Under 35 | 50-69 | 70-79 | Total | ||
| Modal age | 80-84 | 7 | 8 | 19 | 34 |
| 85-89 | 2 | 5 | 8 | 15 | |
| 90-94 | 4 | 3 | 2 | 9 | |
| 95-99 | 0 | 3 | 0 | 3 | |
| Total | 13 | 19 | 29 | 61 | |
| Source: Office for National Statistics - Longitudinal Study | |||||
Download this table Table 21: Modal age by 2011 Census age: Cases where 2011 Census age is below 80 but mode is 80 and over and probability mode is correct is 0.7 or above
.xls (27.1 kB)
Table 22: Final adjusted sample
| 2011 Census age | Number |
| 80-84 | 14,246 |
| 85-89 | 8,620 |
| 90-94 | 3,477 |
| 95-99 | 824 |
| 100+ | 106 |
| Total | 27,273 |
| Source: Office for National Statistics to Longitudinal Study | |
Download this table Table 22: Final adjusted sample
.xls (26.1 kB)The resulting sample age distributions are close to the original ONS-LS sample. They are also close to the published 2011 Census estimates (Table 23).
Table 23: Age distributions at age 80 and over: Office for National Statistics Longitudinal Study (ONS-LS sample, original and revised and 2011 Census estimate
| Original sample | Revised sample | 2011 Census estimate | ||||||
| Number | % | Number | % | difference | % difference | Number | % | |
| 80-84 | 14239 | 52.1 | 14,246 | 52.2 | 7 | 0.05 | 1,338,005 | 51.6 |
| 85-89 | 8646 | 31.7 | 8,620 | 31.6 | -26 | -0.3 | 825,671 | 31.8 |
| 90-94 | 3466 | 12.7 | 3,477 | 12.7 | 11 | 0.3 | 333,455 | 12.9 |
| 95-99 | 842 | 3.1 | 824 | 3 | -18 | -2.1 | 84,376 | 3.3 |
| 100+ | 114 | 0.4 | 106 | 0.4 | -8 | -7.0 | 11,186 | 0.4 |
| Totals | 27307 | 100 | 27,273 | 100 | -34 | -0.1 | 2592693 | 100 |
| Source: Office for National Statistics Longitudinal Study and 2011 Census | ||||||||
Download this table Table 23: Age distributions at age 80 and over: Office for National Statistics Longitudinal Study (ONS-LS sample, original and revised and 2011 Census estimate
.xls (28.2 kB)However, the numbers in the revised sample are slightly lower; the 80 to 89 age category by -0.1% and the 90 and over age category by -0.3%.This implies there may be slightly too many people in the 2011 Census estimate at the oldest ages.
Although the accuracy of the 2011 Census recorded year of birth and derived age data for those aged 80 and over has been shown to be very high, there is some level of inaccuracy; for 1.1% of cases the 2011 Census was not the modal year of birth. The ONS-LS is a representative sample of the 2011 Census. The results therefore imply that there could be around a 1.1% error in recorded age in the 2011 Census records of those aged 80 and over. This increases to 1.9% in the Census records of those aged 90 and over.
As stated earlier, the Office for National Statistics Longitudinal Study (ONS-LS) sample is drawn by selecting everyone with 1 of 4 dates of birth (day/month) enumerated in the Census (pre-imputation). This yields a 1.1% sample of the census count (4/365.25*100, allowing for leap years).
A sampling fraction value below 1.1% indicates fewer LS members in that subgroup than we would expect, given the size of that group enumerated at the 2011 Census. Conversely, a sampling fraction value above 1.1% indicates that there are more LS members in that subgroup than we would expect given the size of that group enumerated at the census16.
The observed sampling fractions in the ONS-LS for both the original research sample and the revised sample are 1.1% for the age 80 to 89 age group and 1.08% for the age 90 and over age group. These figures imply that the 2011 Census count of those aged 90 and over could be inflated by around 2%.This situation could arise if the inflation was a result of issues that do not generate ONS-LS birthdates. However, it could also be that the 4 ONS-LS selection dates are not representative of the birth patterns of the age 90 and over age cohorts, and this could account for the observed results.
It is well documented that there was an uneven pattern of births for the 1919 to 1920 birth cohort. Also there is evidence that deaths by month of death were not evenly distributed for those aged 105 and over (see deaths section). We will be doing further work to validate the date of birth and deaths of those aged 90 and over early in 2017. This will also allow us to test whether births and deaths of those dying at ages 90 and over as a whole are evenly distributed. We could also draw ONS-LS samples of those cohorts aged 90 and over at the time of the 2011 Census from previous censuses (for example, those aged 60 and over in 1981) to check the ONS-LS sampling fractions for these cohorts at those time points to help assess whether or not they have similar sampling fractions to that found in 2011.
Summary and conclusions
The research to date shows that there is a high degree of accuracy in year of birth data (and derived age) in census records for those aged 80 and over in the ONS-LS sample. Given that the ONS-LS is a representative sample of the 2011 Census records, this implies that there is a high degree of accuracy in the year of birth data of those aged 80 and over in the 2011 Census as a whole.
The research identified some level of inaccuracy in the year of birth data in the sample. The year of birth recorded in the 2011 Census was not the modal year of birth across all available records for 1.1% of cases for those aged 80 and over in the ONS-LS and the reliability of the 2011 Census year of birth data decreased with age (for the 80 and over age group).
Annual mid-year estimates are produced by the cohort component method. Those aged 90 and over are treated as 1 group as it is recognised that single year census estimates of those at the oldest ages would not be sufficiently reliable to apply this methodology. The KT methodology is therefore used to distribute the mid-year estimate (MYE) age 90 and over totals.
The analysis reported above suggested that the 2011 Census age 90 and over estimates may be a little too high. However, it is not possible to definitively draw this conclusion as the results could be due to other factors described above. Even a small over-count in the 2011 estimates of those aged 90 and over when rolled forward would result in much larger errors in the rolled forward population estimates at the time of the next census in 2021.
Further analysis
There were 941 cases in the 2011 Census records of those aged 80 and over who appeared for the first time in the 2011 Census cases with no previous census records.
We would expect some level of error in the ONS-LS sample. There will always be some cases where the respondent or proxy respondent has given an incorrect birth date that happens to be one of the 4 dates used to select the ONS-LS sample and similarly where an incorrect birthday is given that means the respondent is not selected when they should have been. The assumption is that these 2 kinds of error cancel each other out. Drawing samples from previous censuses and analysing these longitudinally, including looking at any death and embarkation records, would allow us to go some way towards testing this assumption. This would also enable us to check the representativeness of the ONS-LS sampling fractions for the 90 and over age cohorts in the 2011 Census by comparing with those at earlier time points.
Looking ahead to 2021
It is not possible to obtain a perfect census estimate of the oldest old. Respondent or proxy misreporting due to age exaggeration, lack of knowledge or mis-remembering is difficult to mitigate.
In 2021, the main mode of data collection for the 2021 Census will be online. This will provide both an opportunity and a challenge in obtaining more accurate estimates of the oldest old. Older people are the least likely group in the population to have access to and/or use the internet. This means they will be a particularly “hard to count” group. A lot of effort will be required to ensure appropriate support is in place. On the other hand, an online census provides an opportunity to capture more accurate date of birth data, through for example, date of birth and age validation checks. There were known scanning errors in the 2011 Census that were likely to have impacted disproportionally on the quality of the oldest old estimates. As there is likely to be a significant reduction in the percentage of paper returns in 2021 the effect of this error should be significantly reduced. Also, this research has suggested a number of additional quality checks which could be introduced to help identify any discrepancies from expected values at an early stage of the data capture process.
Next steps
Findings from the above analysis should feed into research on date of birth capture and accuracy for the 2021 Census.
Notes for A2. Quality of Census data at older ages
- 2011 Census confidence intervals
- Thatcher,.R. (Registrar General (1981), Centenarians. Population Trends 25, pp11-14
- Thatcher,.R. (Registrar General (1984), 1981 estimate. Population Trends 38, pp12-13
- Thatcher,.R. (Registrar General (1994), 1991 estimates. Population Trends 75, pp 30-32
- Dini, E. And Goldring,S. (2008), Estimating the changing population of the oldest old. Population Trends 132, pp 8-16
- Methodology and Quality in the ONS (LS) information.
- An assumption was made that the ONS-LS sampling was done correctly
- MIDAS replaced the NHSCR
- MIDAS extract taken in September 2015.
- It is not possible to check if this is the explanation as researchers are not permitted to know the ONS-LS sample selection birth dates
- For cases with multiple cancer and embarkation records only the first instances were considered in the analysis
- 2011 Census Quality Report
- Some date of birth (dob) errors for supposed centenarians were identified and corrected during the census processing stage. Although the core LS file was drawn from the census records prior to these corrections, dob in the final LS research sample used in this analysis was taken from the file where some corrections to dob had been applied.
- The 5 cases where derived age for the MIDAS record was 80 but 2011 Census age was 79 were not included as it was not possible to establish which age was correct.
- If births and deaths are evenly distributed over the year, any age-group in the ONS LS sample should be 1.1% of the Census count. However, if births and deaths of an age group are not evenly distributed over the year, a different ONS-LS sampling fraction could in fact be representative of that age-group depending on the actual (unknown) ONS-LS selection dates.
- Quality and Methodology Information for Annual Mid-Year Population Estimates
7. A3. Quality of migration data at older ages
Introduction
The age 90 and over total population estimate in the annual mid-year population estimate (MYE) is the census estimate of those aged 90 and over (aged on) minus deaths, plus net migration. The quality of the mid-year estimate of those aged 90 and over is therefore dependent on the quality of the census estimate, deaths data and migration data at the oldest ages.
The MYE of the population includes 2 migration components – net internal migration and net international migration. At the England and Wales level, net internal migration comprises UK cross-border flows only. This section of the report examines the quality of net UK cross-border migration and international migration data for those aged 80 and over used in the production of the mid-year estimates of the oldest population1.
Migration within England and Wales and cross internal UK borders
The internal migration component of the MYE includes both moves within England and Wales and cross internal UK border moves.
Internal migration estimates are primarily based on patient register (PR) data that flags up when people change their address. Since most people re-register with a new doctor after moving, these data are considered to provide a good proxy indicator of migration.
The broad approach is to use the annual extracts of PR data to identify people by age and sex who have moved between local authorities and across internal UK borders since the previous mid-year. The National Health Service Central Register (NHSCR) for England and Wales (for which we receive information weekly) provides additional PR information which is used to estimate PR moves not picked up from the annual PR extracts. The NHSCR would be an insufficient source in its own right as the data are only available for former health authorities rather than local authorities).
The estimated UK cross border in-migrants by age and sex obtained from the PR is constrained to the total number of moves from Northern Ireland and from Scotland into England and Wales derived from the NHSCR. The number of moves from England and Wales to Northern Ireland is derived from the Northern Irish medical card register totals supplied by the Northern Ireland Statistics and Research Agency (NISRA) and data on moves from England and Wales to Scotland are derived from the Scottish NHSCR totals supplied by National Records of Scotland (NRS). The total flows to and from constituent countries of the UK are agreed between ourselves, NRS and NISRA, based on records of in-migration to the relevant country.
The key limitation of the NHS data used to estimate internal migration is that some people don’t register promptly with a new General Practitioner (GP) after they move, and some people may never register with a GP at all. This may be less of any issue for the older population as they are more likely to be in poorer health than the general population and therefore more likely to be registered with a GP. Other known quality issues include time lag in processing death registrations. This will particularly affect older population numbers due to their higher mortality rate.
What is the level of UK cross-border migration at the oldest ages?
Net UK cross-border flows in and out of England and Wales are low at the oldest ages (Figure 3).
Figure 3: Net cross-UK border migration to England and Wales at ages 80 and over, 2002 to 2014
England and Wales
Source: 2014 Mid-year population estimates components of change
Download this chart Figure 3: Net cross-UK border migration to England and Wales at ages 80 and over, 2002 to 2014
Image .csv .xlsOver the period 2002 to 2014, net cross-border flows at the oldest ages have been negative (that is, more people have moved from England and Wales to Scotland or Northern Ireland than have moved from those countries to England and Wales). At ages 80 to 89, year-on-year net cross-border flows have varied between around -340 people to -65 (-0.02% and -0.003% of the population aged in their 80s). At ages 90 and over flows have ranged from -110 to -35 (-0.03% and -0.01%) of the age 90 and over population.
Quality of the cross-UK border migration estimates at the oldest ages
To give an indication of the quality of the UK cross-border migration, estimates obtained from PR data were compared with data obtained from the 2011 Census from responses to the question “What was your address 1 year ago?” (Table 24). The England and Wales census does not provide a measure of the numbers of out-migrants by age; however, data on in-migration from England and Wales to Scotland and Northern Ireland is available from the censuses taken in Scotland and Northern Ireland.
Table 24: Cross-UK border migration at ages 80 and over, 2011
| Cross UK border migration, NHS/PR data1 mid-2011 | Cross UK border migration, 2011 Census data, March 2011 | ||||
| Age group | In-migration; to E and W Persons-in | Out-migration; from E and W Persons-out | In-migration; to E and W Persons-in | Out-migration; from E and W Persons-out | |
| Northern Ireland | 80 to 89 | 53 | 48 | 47 | 59 |
| 90 and over | 6 | 15 | 10 | 16 | |
| Scotland | 80 to 89 | 442 | 529 | 423 | 419 |
| 90 and over | 89 | 145 | 100 | 119 | |
| Source: NHS Patient Register; 2011 Census | |||||
| Notes: | |||||
| 1. Note there is a 3 month difference between the data sources | |||||
| 2. E and W refers to England and Wales. | |||||
Download this table Table 24: Cross-UK border migration at ages 80 and over, 2011
.xls (27.6 kB)Net flows are in different directions for the 80 to 89 age group in the 2 data sources; however, overall the estimates are of similar magnitude and are very small relative to the population suggesting that the quality of UK cross-border migration data at the oldest ages used in the production of the mid-year estimates is acceptable.
International migration
Our national estimates of international migration are based on the International Passenger Survey (IPS). The IPS is a sample survey which interviews around 700,000 people annually, of which around 4,000 are identified as long-term international migrants. The migrant respondents are scaled to produce national migration estimates using a complex weighting system.
a) International immigration component of the mid-year estimates (MYEs)
Responses to the 2011 Census question “What was your address 1 year ago?” are used to obtain a single year of age and sex distribution of immigrants. This is applied and constrained to the national long-term international migration in-flow total derived from the IPS.
b) International emigration component of the MYEs
International emigration figures used in the production of the MYEs are obtained from the national long-term international migration out-flow total derived from the IPS. Three years of IPS data (current year and previous 2 years) are then used to provide a detailed single year of age distribution by sex.
Quality of the international migration component of MYEs at the oldest ages
The current method for the break-down of the immigration estimates by age and sex was implemented in 2013 (for the 2012 MYE) following an internal review. Prior to this time, immigration estimates were constrained to IPS national quinary age totals. The review found that the small sample size in the IPS resulted in an unreliable age distribution, with older people one of the age groups particularly affected as evidenced when compared with results from the 2011 Census address 1 year ago question (Figure 4 and Table 25). The change in method has resulted in an increase in the estimated number of immigrants at the oldest ages within the MYEs.
Figure 4: International immigration at the oldest ages in mid-year estimate, 2004 to 2014
England and Wales
Source: 2014 Mid-year population estimates, components of change
Download this chart Figure 4: International immigration at the oldest ages in mid-year estimate, 2004 to 2014
Image .csv .xls
Table 25: All usual residents living in England and Wales on Census day 2011 who were living outside of the UK one year previously
| Residence one year previously | Age group | Persons |
| Outside of the UK | 80 to 89 | 2,488 |
| 90 and over | 362 | |
| Source: 2011 Census | ||
| Notes: | ||
| 1. UK consists of England, Wales, Scotland and Northern Ireland. Outside of UK is all other countries including Channel Islands and Isle of Man. | ||
Download this table Table 25: All usual residents living in England and Wales on Census day 2011 who were living outside of the UK one year previously
.xls (18.4 kB)At age 80 and over the flows of migrants both to and from England and Wales are too small to be reliably measured by the IPS. This means that estimates of migration at ages 80 and over derived from the IPS are subject to wide confidence intervals. The implementation of the new method in 2012 (using the 2011 Census age and sex distribution of immigrants applied to IPS immigration estimates) improves the estimates of immigration for older people (dependent on the accuracy of the information in the 2011 Census - see previous section). However, emigration by single year of age is still solely determined by the IPS, making these the weakest component of the MYE of older people.
What is the level of international migration at the oldest ages?
Net international migration at the oldest ages is very low and accounts for only a very small proportion of total international migration. Over the period 2012 to 2014, international migration at ages 80 to 89 averaged 1% of the total and at ages 90 and over averaged 0.2% of the total within the MYE (Figure 5).
Figure 5: Net international migration by age groups, MYE components, 2012 to 2014
England and Wales
Source: Office for National Statistics
Download this chart Figure 5: Net international migration by age groups, MYE components, 2012 to 2014
Image .csv .xlsOver the period 2012 to 20142 there was an increase from just under 1,500 to just over 2,000 in annual net international migration at ages 80 to 89 (Figure 6). (This equates to an increase from 0.06% to 0.1% of the population aged 80-89 and over.) This increase could be due to improvements in the method used to estimate the immigration component of population estimates with no equivalent improvement for the emigration estimate component.
Net international migration at ages 90 and over remained more or less stable over the same period at around 350 people per year (around 0.07% of the population aged 90 and over each year).
Figure 6: Net international migration at ages 80 and over, 2012 to 2014
England and Wales
Source: Office for National Statistics
Download this chart Figure 6: Net international migration at ages 80 and over, 2012 to 2014
Image .csv .xlsAt very old ages, numbers of international and UK cross-border migrants to and from England and Wales are very low, meaning that migration accounts for a very small proportion of the annual mid-year population estimate (Table 26).
Table 26: Net migration component of population change, England and Wales, 2013 to 2014
| Age group | Change in population | Net UK cross border migration | Net international migration | Total net migration |
| 2013 / 2014 | 2013 / 2014 | 2013 / 2014 | ||
| 80 to 89 | 33,687 | -76 (-0.2%) | 2,142 (6.4%) | 2,066 (6.1%) |
| 90 and over | 21,013 | -34 (-0.2%) | 364 (1.7%) | 330 (1.6%) |
| Source: Office for National Statistics | ||||
Download this table Table 26: Net migration component of population change, England and Wales, 2013 to 2014
.xls (27.1 kB)Only 6.1% and 1.6% of the overall change in the population aged 80 to 89 and 90 and over respectively in 2013 and 2014 were due to internal and international migration combined.
Summary and conclusions
The quality of UK cross-border migration data at the oldest ages appears to be reasonably good. The quality of international immigration data at the very oldest ages also appears reasonable since the method change introduced in 2013 (2012 MYE); however, emigration data at the oldest ages is likely to be of poorer quality. This in turn impacts on the quality of net migration figures at the oldest ages within the MYEs.
However, levels of UK cross-border migration at the oldest ages are very low. Levels of international migration are higher but still low. Migration, therefore, has minimal impact on the annual MYE of those aged 90 and over.
Next steps
Following the change in method reported above, immigration and emigration figures at the oldest ages are less “balanced” than previously within the MYE. Further work is needed to assess the impact of this change on high-age population estimates and whether any further work could be carried out to improve emigration estimates at the oldest ages within population estimates.
Work is also planned to look at the age and sex distribution of migrants using administrative data sources to assess whether this has changed since 2011.
Notes for A3. Quality of migration data at older ages
Quality and Methodology Information for Annual Mid-Year Population Estimates
2012 to 2014 only shown as 2012 was year change was made to the way age/sex distributions were applied to immigration estimates as described earlier in the report section.
8. Section B: How good is the Kannisto-Thatcher (KT) method?
Thatcher et al (2002) considered various methods proposed for estimating single year of age populations at the oldest ages before concluding that, of those surveyed, the survivor ratio with the amendments proposed in the paper (the KT method) performed the best when applied to actual population data.
However, we do not know how accurate the KT methodology actually is or the sensitivity of the results to the accuracy of the deaths data used or the levels of migration at the oldest ages. This leads to the questions:
How accurate are the KT estimates?
How much does imperfect input data impair the quality of KT estimates?
This section firstly describes the KT method and then examines these 2 questions.
Back to table of contents9. B1. Description of the KT method of calculation
Population estimates of those aged 90 and over by single year of age are constructed using the Kannisto-Thatcher (KT) model which is a version of survivor-ratio methodology1. The KT method produces age-specific estimates of population at older ages using deaths data.
At high ages and for dates sufficiently far in the past, age specific population estimates can be obtained directly from deaths data. Once all the members of a given birth cohort have died it is possible to reconstruct the numbers who were alive at earlier dates from their dates of birth and death.
For cohorts which are almost extinct the ratio of the number of survivors who are still alive to the numbers in the cohort who died in the previous “k” years can be estimated from the experience of previous cohorts. This estimated survivor ratio can then be applied to the known number of deaths in the given cohort which occurred over the last “k” years. The past population for this cohort can then be recreated by adding back the deaths. If the highest age “x” at which there is expected to be a survivor is known, the whole process can be repeated to obtain survivor ratios to estimate the numbers aged x-1, then x-2 and so on, in an iterative process.
Applying this method directly assumes that the survivor ratio is the same as that in the immediately preceding cohort. However, this may be an atypical cohort for various reasons. In order to damp fluctuations in the ratios, the average survivor ratio over the preceding “m” cohorts can be calculated, rather than just a single cohort.
In circumstances where mortality rates are changing over time, or where estimates are required down to ages as low as 90, Kannisto and Thatcher proposed various modifications to the survivor ratio method. To compensate for the fact that reduced mortality at higher ages may increase the size of the survivor ratio over time, a correction factor is applied to the survivor ratios calculated. This can be set to constrain the estimates to sum to the official population estimate for a given age group (say, 90 and over) or so that the estimates join to the official estimates in a specific way.
Our current methodology
Our current methodology follows the Kannisto-Thatcher (KT) method described above, with values k=5 and m=5 and a constraint that the total estimates derived for the most recent year being estimated sum to the official 90 and over population estimate for that year.
To carry out the calculations, deaths data has to be in the format of deaths during the annual period by age at the start of the period. For England and Wales, deaths are published by calendar year by age at death whilst population estimates are published at a mid-year date. Hence both the deaths data, which are deaths in a calendar year by age at death, and the population estimates, which are mid-year rather than as at 1 January, have to be adjusted into the required format.
In practice, in producing the age-specific population estimates for mid-year T, our methodology adjusts population estimates to age last birthday at the beginning of the calendar year (that is, at 1 January T) by interpolating the mid-year estimates for years T-1 and T. Hence if the population aged x at mid-year T is P(x,T), the number aged x at 1 January T is taken to be 0.5 x [P(x,T-1)+P(x,T)].
In order to calculate the survivor ratios, deaths data are converted into the required format for year T and earlier years by assuming that half of the deaths age x in a given year Y were of people aged x-1 at 1 January Y and half were aged x at 1 January Y. Hence, if the number of deaths of people aged x in calendar year Y is D(x,Y), the number of deaths in calendar year Y of people aged x at 1 January Y is assumed to be 0.5 x [D(x,Y)+D(x+1,Y)].
The method as used by ONS can be expressed as follows.
For all years prior to the year that is being calculated: (where Px is population age x and the beginning of the year, Dx is the number of deaths during the year age x at the beginning of the year, x is age and T is year):
For the year under consideration (where c is the correction factor, S is the survival ratio and T is the ”current” year):
where S is calculated as:
The calculations are performed sequentially for single years of age, starting with the oldest age beyond which no-one is assumed to survive, taken to be 120.
The value of the correction factor c is derived such that:
where E is the “official” population estimate of the population aged 90 and over at 1January T obtained by interpolating the official 90 and over estimates at 1 mid-year T-1 and mid-year T.
The methodology produces single year of age estimates at 1January T. These are then aged on to 1 January T+1 by subtracting the deaths during year T by age at 1January T. The mid-year population estimates for year T and earlier years are then derived by interpolation. Rating factors are then applied to the derived mid-year estimates such that they total to the official estimates for that year.
Testing the Kannisto-Thatcher (KT) assumptions
The KT method requires making certain assumptions.
Migration at the oldest ages is minimal and so will not invalidate the results
There is some migration at the oldest ages but levels are very low. Over the period 2012 to 2014, total net migration at ages 90 and over averaged around 350 people per year, around 0.07% of the 90 and over population (see Migration data section).
Information on age at death is accurate and deaths data are complete
Deaths data appears to be of high quality but it cannot be assumed to be wholly accurate or complete.
“Age at death” data were found to be of very high quality for those dying aged 105 and over in England and Wales who were born in England and Wales (See Deaths data section). We do not know if this holds for those dying at younger old ages. Also we do not know the level of error in age at death data for those born outside of England and Wales. (15% of male and 8% of female deaths in the research sample of those aged 105 and over were of people born outside the UK, or no place of birth recorded. In total, 10% of those who died aged 90 and over in 2014 in England and Wales were born outside of England and Wales.)
Late registrations mean that not all deaths are captured in the annual occurrence deaths datasets used in the production of the KT estimates.
Additionally, for our calculations, it is assumed that a 50:50 split of deaths age last birthday in a calendar year is reasonable.
The method we currently use makes the assumption in the KT methodology that both births of those who attain very old ages and deaths of these people are evenly spread through the year. The deaths data is adjusted to the required format by assuming that half of the deaths age x in year T were aged x-1 at 1January T and half were aged x at 1January T. These approximations could result in errors in the results.
Further analysis has been carried out on the dataset comprising those deaths for males born in England and Wales where a fully matching birth record or 1 that matched apart from probable transcription errors (313 cases in total) and similarly for females (797 cases including the 2 cases where a slightly incorrect year of birth was recorded) (See section A1). Male and female deaths have been combined to increase the sample size. The numbers of deaths by month of birth and month of death for the periods January to June and July to December, together with the expected numbers if the births and deaths were evenly distributed over the 2 halves of the year are shown in Table 27.
Table 27: Semi-supercentenarian sample deaths by month of birth and death
| Number of deaths by month of birth | Number of deaths by month of death | Expected number of deaths by month of birth and month of death, if evenly distributed | |
| Jan to June | 546 | 588 | 550.4 |
| July to Dec | 564 | 522 | 559.6 |
| Total | 1,110 | 1,110 | 1,110 |
| Source: Office for National Statistics | |||
Download this table Table 27: Semi-supercentenarian sample deaths by month of birth and death
.xls (17.9 kB)A chi-square test was performed. Differences between the observed and expected number of deaths by month of birth were not statistically significant; however, the differences between the observed and expected number of deaths by month of death were statistically significant (p<0.05).
The possible effects of the adjustment made to deaths data in our method on the resulting KT 90 and over population estimates has been tested using data for Finland. Results are reported in Section B2.
Notes for B1. Description of the KT method of calculation
- Thatcher, R. Kannisto, V. Andreev, K.F. (2002) The Survivor Ratio Method for Estimating Numbers at High Ages. Demographic Research, Vol 6, 1-18
10. B2: Accuracy
The accuracy of Kannisto-Thatcher (KT) estimates can be assessed by comparing them against other population figures. However, the official age 90 and over aggregate population mid-year estimates (MYE) published by ONS have known weaknesses. They are based on the most recent census estimates which are then rolled forward allowing for deaths and net migration. Potential issues with obtaining an accurate estimate of the age 90 and over population in censuses were discussed in the Census section). Comparing the age 90 and over total population KT estimate with the official MYE age 90 and over population estimates, therefore, may not be a good indicator of the quality of the KT estimates.
In general, the better the comparator population estimates, the better the quality of the KT estimates can be assessed. Finland and Sweden have population registers which are known for their very high quality1 (and, in particular, with better data on migration than that available for England and Wales). KT estimates using deaths data from these countries have been derived and compared to the register population counts.
Input data
Our population estimates refer to the population size at mid-year (30 June). Age 90 and over population estimates by single year of age are therefore needed for the mid-year point as well. For a strict application of the KT methodology, deaths data for 12-month periods running from mid-year to mid-year by age at the start of the 12-month period are required. Our approach is to produce population estimates as at 1 January and then interpolate these to obtain the MYE. Working with population estimates as at 1 January, the format of the deaths data required is deaths in a calendar year by age at the start of the calendar year.
We receive deaths data by calendar year by age at death. This is not necessarily the same as age at the start of the calendar year death occurred; if the person died after their birthday during the year, their age at death would be 1 year older than their age at the start of the calendar year. In order to obtain the deaths data in the format required it is assumed that deaths and birthdays occur evenly throughout a calendar year. As a result, half the people are assumed to have died before their birthday in the reference year, and half after their birthday. Deciding whether this is a good approximation requires comparing KT estimates produced using this assumption with estimates produced using deaths data grouped by age at the start of the calendar year.
Population estimates for Sweden are produced as at 31 December and for Finland as at 1 January. Deaths data are published by calendar year by age at death up to age 99 and 100 and over for Sweden2 and up to age 112 for Finland. Sweden also publishes deaths data in the format required, but again only up to age 99 and 100 and over. However, deaths data by age at the reference day of the population estimates (31 December for Sweden, 1 January for Finland) have also been obtained directly from the National Statistical Institutes (NSIs) in Sweden and Finland.
KT estimates compared with register-based population estimates
2014-based KT estimates were produced for both Sweden and Finland using deaths data in the required format, that is, deaths by age at reference date. Deaths data were available by single year of age up to the highest age of death for both countries and back to 1980 for Finland and back to 1968 for Sweden3. Population register data was available by single year of age up to age 99 and age 100 and over for both countries.
The KT age 90 and over population totals for Sweden and Finland were compared with the population register counts for those aged 90 and over in the respective country’s population registers (Figures 7 and 8).
Figure 7: Kannisto-Thatcher and population register estimates of the 90 and over population, 1968 to 2014
Sweden
Source: Office for National Statistics calculations based on Statistics Sweden data
Download this chart Figure 7: Kannisto-Thatcher and population register estimates of the 90 and over population, 1968 to 2014
Image .csv .xls
Figure 8: Kannisto-Thatcher and population register estimates of the 90 and over population, 1980 to 2014
Finland
Source: Office for National Statistics calculations based on Statistics Finland data
Download this chart Figure 8: Kannisto-Thatcher and population register estimates of the 90 and over population, 1980 to 2014
Image .csv .xlsKT estimates of the age 90 and over population total for Sweden and Finland appear to fit the registration data very closely, for both sexes, over the time periods shown.
The percentage differences between KT estimates of the age 90 and over population and the population register counts are shown in Figure 9. A value of zero indicates that the KT estimate and the population register estimate are the same.
Figure 9: Percentage difference between Kannisto-Thatcher estimates and population register estimates for Sweden and Finland
Sweden, 1968 to 2014 Finland, 1980 to 2014
Source: Office for National Statistics calculations based on data from Statistics Sweden and Statistics Finland
Download this chart Figure 9: Percentage difference between Kannisto-Thatcher estimates and population register estimates for Sweden and Finland
Image .csv .xlsFor both countries and both sexes there are differences of less than 1% between the age 90 and over KT estimates and the respective population register counts over the whole period until 2007. After that time the gap between population register totals and KT totals increase. The steep decline in the KT estimate of the age 90 and over population in relation to the official population estimate for the most recent years is also observed when comparing KT estimates for England and Wales with official MYE of the age 90 and over population. Possible causes of this pattern are examined in Section B3.
KT estimates of the age 90 and over population by single year of age for persons were then compared with population register counts for Sweden and Finland. Figure 10 shows the percentage differences between the KT estimates and the register counts over the period 2002 to 2014 for Sweden. Figure 11 shows the percentage differences between the 2 data sources for Finland over the same time period.
Figure 10: Percentage differences between the KT estimates and the register counts
Sweden, 2002 to 2014
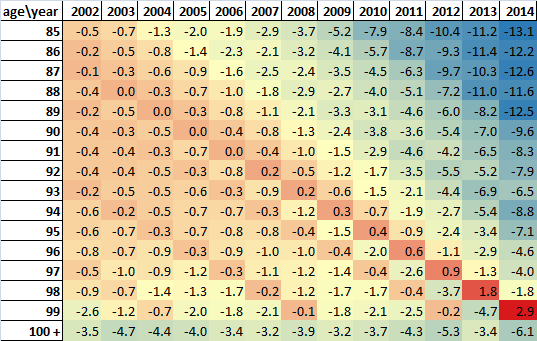
Source: Office for National Statistics calculations based on Statistics Sweden data
Download this image Figure 10: Percentage differences between the KT estimates and the register counts
.png (38.6 kB) .xls (19.5 kB)
Figure 11: Percentage differences between the KT estimates and the register counts
Finland, 2002 to 2014
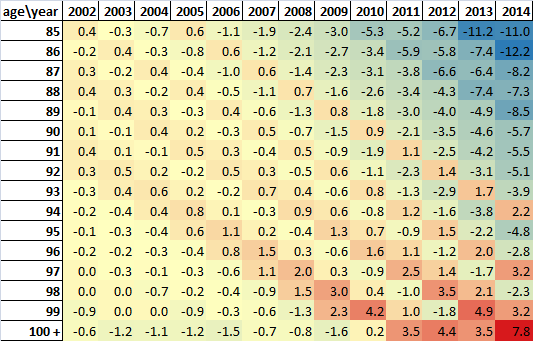
Source: Office for National Statistics calculations based on Statistics Finland data
Download this image Figure 11: Percentage differences between the KT estimates and the register counts
.png (41.1 kB) .xls (19.5 kB)The background colours in the charts are determined by the size of the value represented. Values with a yellow background indicate very small differences; the more blue the background, the larger the under estimation of the KTs in comparison to the population register counts; the more red the background the larger the overestimation.
For both Sweden and Finland, the ”fit” between the KT estimates and the population register counts is generally very good at all ages across time but deteriorates with distance to cohort extinction, that is, the largest differences are for the most recent years and at younger ages where more of the population are yet to die and therefore deaths data is less complete.
The average (mean) percentage deviations between the KT estimates and population register counts at each age across all available years by sex were then calculated to provide summary measures. These are shown in Figure 12 for Sweden and in Figure 13 for Finland.
Figure 12: Average percentage deviation of Kannisto-Thatcher estimates from population register estimates by age, 1980 to 2014
Finland
Source: Office for National Statistics calculations based on Statistics Finland data
Download this chart Figure 12: Average percentage deviation of Kannisto-Thatcher estimates from population register estimates by age, 1980 to 2014
Image .csv .xlsOn average the fit between the KT estimates and the population register counts for Sweden is good across all ages with a maximum deviation of around -2.0% for males up to age 99 and a maximum of around -1.5% across all ages for females.
For males the fit gets better by age up to age 94 and then starts to decline, dropping steeply at the oldest ages. The pattern is the same for females but the decline in fit starts a few years later. The improvement in fit from the youngest ages is due to the influence of the relatively large deviations at the younger ages for the most recent years where deaths data is less complete (Figure x). The decline in fit at the oldest ages is probably because even small deviations between the KTs and population register counts at the very oldest ages represent a relatively large percentage difference due to small numbers at these ages. This decline is probably less steep for females and happens later because although numbers are relatively small at the oldest ages they are larger than for males at these ages.
Figure 13: Average percentage deviation of Kannisto-Thatcher estimates from population register estimates by age, 1980 to 2014
Finland
Source: Office for National Statistics calculations based on Statistics Finland data
Download this chart Figure 13: Average percentage deviation of Kannisto-Thatcher estimates from population register estimates by age, 1980 to 2014
Image .csv .xlsOn average across all available years of data, the fit between the KT estimates and the population register counts for Finland by single year of age are very close. For males there is a maximum deviation of -1.5% across all ages; for females, deviations range from -1.4% to +0.3%. The pattern is similar to that for Sweden with the goodness of fit for both males and females increasing from the youngest ages to the late 90s. At the very oldest ages the pattern is more volatile due to small sample sizes.
Overall the KT estimates produced for both Sweden and Finland are close to population register counts of the age 90 and over population, suggesting that the KT method provides a good estimate of the population when the input deaths data is in the required format. However, performance declines with distance to cohort extinction; that is, the estimates are worse for more recent years and for younger ages. This pattern is more evident in the data for Sweden than for Finland.
How much impact does not having deaths data in the required format have on the quality of KT estimates?
As described earlier, we input deaths data for producing KT estimates for England and Wales is deaths by age at death by calendar year. To obtain the deaths data in the required format for the KT methodology half the people are assumed to have died before their birthday in the reference year, and half after their birthday.
Deaths data by both age at reference data and by age at death by calendar year are available for Finland4. These data were used to test the possible effects of the assumption made in the preparation of age at deaths data for England and Wales to produce the England and Wales KT estimates on the resulting KT estimates.
KT estimates were produced for Finland from deaths data by age at death (converted into the required format by assuming that half of the deaths age x in a given year Y were aged x-1 at 1 January Y and half were aged x at 1 January Y) and also from deaths data by age at the reference date. The resulting 2 sets of KT estimates were compared and in turn these were compared with the Finland population register counts.
Figure 14: Differences between Kannisto-Thatcher estimates for Finland derived from deaths data on different definitions and Finland population register estimates, 1980 to 2014
Finland
Source: Office for National Statistics calculations based on Statistics Finland data
Download this chart Figure 14: Differences between Kannisto-Thatcher estimates for Finland derived from deaths data on different definitions and Finland population register estimates, 1980 to 2014
Image .csv .xlsFigure 14 compares percentage differences between KT estimates produced from deaths data by age at the reference date and population register counts with the percentage differences between KT estimates produced from deaths data by age at death and population register counts. The zero line indicates no differences between the KT estimates and the register count.
The “fit” between the KT estimates produced from the age at deaths data and the population register counts is not as good as that for the KTs produced from deaths data with the correct age definition. However, although the fit is more erratic and the percentage differences between the KT estimates and the population register counts are larger than those between the KTs produced from deaths data with the correct age definition, the differences are still relatively small. Both sets of KTs show the same undercount for the most recent years.
It appears therefore that not having the input deaths data on the correct age definition does have some effect on the quality of the resulting KT estimates but this is relatively minor.
Percentage differences between KT estimates of the age 90 and over total population for England and Wales and the official mid-year estimate (MYE) of the age 90 and over population over the period 1980 to 2014 were then compared with the percentage differences between the KT estimates for Finland produced from deaths data by age at death and the Finland registration counts over the same period (Figure 15).
5The percentage differences between the England and Wales KT estimate age 90 and over totals and the official age 90 and over estimates are considerably larger than those between the Finnish KT age 90 and over estimate totals and the age 90 and over totals in the Finnish population counts.
Figure 15: Percentage difference between Kannisto-Thatcher estimates and official estimates
England and Wales and Finland, 1980 to 2014
Source: Statistics Finland; Office for National Statistics
Download this chart Figure 15: Percentage difference between Kannisto-Thatcher estimates and official estimates
Image .csv .xlsGiven that the KT estimates for both England and Wales and Finland were produced from deaths data in the same format (age at death) and using the same method, this suggests that there is a difference either in the quality of the input deaths data and/or in the quality of the official age 90 and over population estimates for England and Wales and Finland. Deaths registrations are considered very reliable for both Finland and for England and Wales (see section A1). Equally, Finnish population estimates are considered very high quality, being based on a long-standing register6. Assuming the assumption of minimal migration at the oldest ages holds, the results seem to suggest the official MYE of the age 90 and over population for England and Wales may be too high.
Notes for B2: Accuracy
Statistics Finland: Quality descriptions population; Quality descriptions deaths. Statistics Sweden: Description of the population register.
Statistics Sweden advised us that there is a quality issue with some foreign-born people having incorrect birth data in the registry. This is most noticeable for the oldest age groups.
These are deaths data obtained directly from the National Statistical Institutes (NSIs) in Sweden and Finland.
Both Finland and Sweden publish deaths data by age at death but the Swedish deaths data are only available up to age 99 by single year of age; the data for Finland are available up to age 112.
KT estimates produced for England and Wales are constrained to the official 90 and over mid-year estimates total prior to publication as the output Estimates of the Very Old.
Statistics Finland: Quality descriptions population
11. B3: Population modelling
Although Swedish and Finnish data are believed to be of very high quality it is still possible that there are some errors in the data (for example, for deaths data the age at death (or the date of birth) may be incorrectly reported or not known). There is also likely to be some migration at the older ages. Another way to assess the accuracy of the KT method has therefore been investigated involving the construction of model populations at these older ages under which it is assumed there is no migration. The only inflow is the assumed numbers entering the population each year at the youngest age in the model, and the only exit from the population being death. The deaths and populations are in the age and time definitions required. This allows conclusions to be drawn about the KT methodology without caveats relating to the format of the underlying data or assumptions on migration at the oldest ages.
The underlying mortality rates and/or the numbers in each birth cohort entering at the youngest age in the model can be varied to derive a set of model populations. The accuracy of the KT method can then be tested by comparing the estimates produced by the KT method against the model population (where the population estimates are known to be correct). The model populations can be used to assess the effectiveness of modifications applied to the KT method and also to test whether other approaches may produce better results. They can also be amended to allow for net migration and hence assess the sensitivity of the KT results to the levels of migration at the older ages.
A series of simplified model populations have been constructed for the age range 80 to 125 for the period 1991 to 2013 as follows:
A starting population by single year of age 80 to 125 at 1 January 1991 is constructed together with age-specific mortality rates for 1991. All the model populations constructed have the same assumed starting population and the same age-specific mortality rates for 1991 (in this case the probability of someone aged x at 1 January 1991 dying before reaching age x+1 at 1 January 1992). The mortality rates are projected forward for future years using various assumptions on improvements in mortality each year. The resulting mortality rates are then applied to the starting population, together with assumed number of persons entering at age 80 on 1 January in each future year to project the age-specific resulting population at 1 January in each future year up to 2013 as follows:
Let
Let
Let
Then
where
is assumed to be 1.000 in all years so everyone aged 125 at the start of the year is assumed to die before reaching age 126 at the start of the following year.
Therefore the only movements assumed are the people entering the population on 1 January each year at age 80 and deaths; it is assumed that there is no migration.
In all, 14 different populations were constructed using a variety of different assumed changes in mortality rates over time and/or numbers of people entering each year aged 80, as follows:
Table 28: Model populations
| Model | Mortality assumption | Change in numbers aged 80 entering each year |
| 1 | No change in rates by year | No change |
| 2 | Mortality rates decrease by 1.0% per annum | No change |
| 3 | No change in rates by year | Increases by 2.0% per annum |
| 4 | Mortality rates decrease by 1.0% per annum | Increases by 2.0% per annum |
| 5 | No change in rates by year | Change by same percentage as in corresponding mid-year estimates for age 80 |
| 6 | Mortality rates decrease by 2.0% per annum | No change |
| 7 | Mortality rates decrease by 2.0% per annum | Change by same percentage as in corresponding mid-year estimates for age 80 |
| 8 | Mortality rates decrease by varying amounts per annum by age. The same rate is assumed for a given year, increasing for each later year | No change |
| 9 | Mortality rates increase by 1.0% per annum | No change |
| 10 | Mortality rates increase by 1.0% per annum | Change by same percentage as in corresponding mid-year estimates for age 80 |
| 11 | Mortality rates decrease by varying amounts per annum by age | No change |
| 12 | Mortality rates decrease by varying amounts per annum by age | Change by same percentage as in corresponding mid-year estimates for age 80 |
| 13 | Mortality rates decrease by 3.0% per annum | No change |
| 14 | Mortality rates increase by 2.0% per annum | No change |
| Source: Office for National Statistics | ||
Download this table Table 28: Model populations
.xls (18.9 kB)For each model, the data for years 1991 to 2012 were input into our KT methodology to obtain 1 January KT population estimates by single year of age for 2013 and preceding years back to 1991.
The KT methodology incorporates a factor which is intended to allow for changes in mortality rates over time. For instance, if mortality rates are improving, then the trend in the survivor ratios will be increasing and survivor ratios calculated from historical data will be lower than if calculated on more recent data. Our methodology uses a parameter, c, which is set so that the sum of the single year of age mid-year estimates for ages 90 and over equals the aggregate total for ages 90 and over for the mid-year.
The following table indicates the value of c required for each model in order that the sum of the single year of age estimates at 1 January 2012 for ages 90 to 125 equals the projected aggregate total for age 90 to 125 at 1 January 2012 in the model population. It also indicates whether the resulting single year of age estimates were higher or lower than that for the model population.
Table 29: Correction factor required for models and comparison of estimates to model populations
| Model | Value for c | KT estimates for ages 90 to 125 compared to model population |
| 1 | 1 | KT estimates exactly the same as for model population at all ages |
| 2 | 1.0592 | KT estimates higher at youngest ages; lower at other ages |
| 3 | 1 | Very small differences at one or two ages |
| 4 | 1.0582 | KT estimates higher at youngest ages; lower at other ages |
| 5 | 1 | Very small differences at one or two ages |
| 6 | 1.1122 | KT estimates higher at youngest ages; lower at other ages |
| 7 | 1.1103 | KT estimates higher at youngest ages; lower at other ages |
| 8 | 1.1449 | KT estimates higher at youngest ages; lower at other ages |
| 9 | 0.9341 | KT estimates lower at youngest ages; higher at other ages |
| 10 | 0.9357 | KT estimates lower at youngest ages; higher at other ages |
| 11 | 1.1056 | KT estimates higher at youngest ages; lower at other ages |
| 12 | 1.104 | KT estimates higher at youngest ages; lower at other ages |
| 13 | 1.161 | KT estimates higher at youngest ages; lower at other ages |
| 14 | 0.8539 | KT estimates lower at youngest ages; higher at other ages |
| Source: Office for National Statistics | ||
Download this table Table 29: Correction factor required for models and comparison of estimates to model populations
.xls (18.9 kB)The results for single year of age estimates for 1 January 2012 are shown below:
If there is no change in age-specific mortality rates over time, c = 1.0000 and the resulting single year of age estimates in 2012 are very close to the model estimates, even if the numbers entering each year at age 80 change over time (models 1, 3 and 5).
If mortality rates reduce over time, c > 1.0000 and the resulting KT single year of age estimates in 2012 are higher than the population model estimates at younger ages and lower at older ages in the range in every case modelled (models 2, 4, 6, 7, 8, 11, 12, 13).
If mortality rates increase over time, c < 1.0000 and the resulting single year of age estimates in 2012 are lower than the model estimates at younger ages and higher at older ages in the range in every case modelled (models 9, 10 and 14).
For a given pattern of change in mortality rates over time, the values of c remain broadly similar even if the numbers entering each year at age 80 are different (models 2 and 4, 6 and 7, 9 and 10, 11 and 12).
Aggregate 90 plus total estimates at 1 January for years 1991 to 2011
A comparison of the KT and model population aggregate total 90 and over estimates has also been carried out for the years 1991 to 2011.
For models assuming no change in mortality the 90 and over KT and model estimates are virtually the same for nearly all ages and years with only a very few minor differences.
For populations where mortality is decreasing, differences occur for most years with the KT estimates being lower than the model population. The differentials reach their highest a few years prior to 2012 then the aggregate differences fall until they virtually disappear for the earliest years 1991 and 1992.
For all the model populations with decreasing mortality rates over time, the differentials between the single year of age KT estimates and the model populations in 2012 are all positive at the youngest ages in the age range and negative at older ages. For 2012 the sum of the differentials at each age 90 to 125 equals close to 0. For the models the differences between the model population estimate and the KT-derived estimate remains constant for a given year of birth as the only movement out of the population is death and there are no issues arising from having to approximate data into the format required for carrying out the KT methodology. Hence the difference in the aggregate total for 2011 is the sum of the single year of age differentials in 2012 for ages 91 to 125, in 2010 the sum of the single year of age differentials in 2012 for ages 92 to 125 etc. As those at the youngest ages drop out going back from 2012, the sums of the differentials turns increasingly negative, meaning that the aggregate KT estimates are increasingly lower than the model population moving back through time for a few years before starting to decrease once all the ages where the KT estimates are higher are below age 90. At the same time the overall age 90 and over total for the model population decreases going back to 1992, leading to a peak differential a few years before 2012.
The KT and model estimates are close for the early years 1991 and 1992 since nearly everyone aged 90 and over in those years will have died before by 1 January 2012 (someone aged 90 at 1 January 1991 would be age 111 at 1 January 2012, if they had survived to that age). Therefore, the KT estimates for these years comprise mainly the sum of deaths for each relevant cohort. As there are assumed to be no errors in the deaths data and no migration in the model population, the sums of deaths give the numbers alive in 1991.
Similar patterns arise for those models where mortality is assumed to increase except that for these, the aggregate KT estimates are generally higher than the model population since the KT estimates are lower than the model population at the younger ages and higher at the older ages. Again, the maximum differentials occur a few years before 2012.
Summary and conclusions
The KT method works well where the data are in the correct format and mortality rates at the oldest ages are not changing over time.
Not having the input deaths data on the correct age definition has a relatively small impact on the quality of the resulting KT estimates.
The KT method makes the assumption that deaths data are of high quality. We know that date of birth information is reasonably accurate for people aged 105 and over who were born in England and Wales. We have no indication of the quality of date of birth information for those dying in England and Wales who were aged 90 to 104 or who were born outside of England and Wales (10% of those dying aged 90 and over in England and Wales in 2014).
Where mortality rates are changing over time at the oldest ages a different method for allowing for changes in mortality in the KT methodology may produce better estimates.
The KT method assumes minimal migration at the oldest ages. If migration at the oldest ages grows, the performance of the method will deteriorate.
Next steps
Explore the possibility of obtaining deaths data by age at start of the mid-year for the production of KT estimates.
Explore different methods for allowing for changes in mortality in the KT method.
Back to table of contents12. Section C: Comparisons to counts derived from administrative data
Introduction
There is no definitive count of the population aged 90 and over in England and Wales. The decennial census estimates are considered to be the most authoritative source of population estimates; however, there are a number of reasons why obtaining an accurate census estimate of the oldest old population is difficult (see Section A2).
We also calculate estimates of the population aged 90 and over from deaths data using a form of survivor-ratio methodology, the Kannisto-Thatcher (KT) method1 (see Section B1).
There are also a number of administrative data sources available that include people aged 90 and over. These include the National Health Service (NHS) Patient Register (PR) and the Department for Work and Pensions’ (DWP) Customer Information System (CIS).
In March 2014, the National Statistician recommended a predominantly online census in 2021 supplemented by the further use of administrative and survey data2. In preparation for this, we are conducting a research programme to assess the quality of a number of administrative datasets and explore whether these data can be used in the production of population estimates for all ages in the future. As part of this research, Statistical Population Datasets (SPDs) have been produced by linking multiple administrative datasets. SPD v1.0 was published in October 2015 as research outputs3 and includes population estimates for several time points. Further research outputs produced using a new methodology, SPD v2.0, were published in November 20164.
The datasets that have been linked in SPD v1.0 are the PR, the CIS and the Higher Education Statistics Agency data (HESA) list of registered higher education students in England and Wales. The rationale for producing SPDs is that these are likely to produce more robust estimates than those available in single administrative data sources.
In this section of the report we look at how counts of those aged 90 and over in SPD v1.0 compare with estimates produced by the KT method and with the official 90 and over population estimates for England and Wales. We use SPD v1.0 (as opposed to SPD v2.0) as counts are available for 2011, 2013, 2014 and 2015 and therefore allow us to compare the SPD counts, census/Mid-year estimate, and KT estimates over time.
Description and quality of the available administrative datasets and SPDs
The PR lists all patients who are registered with an NHS General Practitioner (GP) in England and Wales. The DWP CIS lists all people with a National Insurance (NI) number.
HESA data lists all students who are registered on a higher education course in England and Wales. The SPD V1.0 only includes people who appear on at least 2 of the 3 administrative datasets5. In practice, for the oldest old, a person has to be found on both the PR and the CIS to be included in the SPD.
Although everyone registered with an NHS GP will be on the PR, people who are not registered with a GP, including those that have exclusively private healthcare, will not be on the PR. Also, if a person registered with an NHS GP has not made contact with their surgery for a while and does not respond when contacted, they are marked as potentially absent on the PR. Such marked records on the PR are excluded from SPD v1.0.
The CIS includes anyone who has ever had a NI number. If DWP is informed that a person has died, their date of death is added to the CIS database; however, if a death notification happens late, or not at all, the person will still be in the CIS database.
If a death is reported in 1 of the sources, the person who has died will not be included in SPD V1.0. However, as deaths may be registered late, or there may be a gap between when a death is registered and notice of it appearing on the administrative data, not all people who have died in a given year will have been removed from or flagged on the administrative data at the time it is shared with us. This can potentially inflate counts in an SPD. This type of over-count is likely to disproportionately affect the oldest population due to their higher mortality rate.
Looking ahead, the intention is that a survey may be used in conjunction with linked administrative data in order to adjust for under- or over-coverage of administrative data and produce higher-quality estimates (than would be possible with administrative data alone). This could result in an increase or decrease in the count of older people in SPDs (compared to SPD V1.0).
The quality of the SPDs and source datasets are discussed in detail in a report published in 2015, the Administrative Data Research Report6.
Availability of comparative data sources
SPDs for England and Wales have been produced for 4 time points – Census day 2011, mid-2013, mid-2014 and mid-2015. The SPD estimates are available in quinary age groups up to age 90 and over and down to local administrative area level and small area level. SPD V1.0 estimates by local authority, sex and single year of age up to age 90 are also available at these time points. 2011 Census estimates and official mid-year population estimates for 2013, 2014 and 2015 provide comparator estimates.
Kannisto-Thatcher (KT) estimates for ages 90 and over by single year of age and sex for 2011 (January), mid-2013, mid-2014 and mid-2015 were produced from death registration data using the KT method7. KT estimates for 2011, 2013 and 2014 were taken from the 2002 to 2015 time series. Given it is known that the accuracy of the KT estimates decreases with distance to cohort extinction, this time series provides the best available KT estimates for 2011, 2013 and 2014 (see Section B2).
Analysis and results
a) 90 and over population grouped
At national level, SPD V1.0 estimates for males and females are around 2% lower than official population estimates (2011 Census and mid-year estimates (MYEs)) for most age groups. The exception is for working-age males where the SPD V1.0 estimate is higher than the official estimates. Children and young people aged 5 to 19 and those aged 85 and over8 have the lowest SPD V1.0 estimates compared with the official estimates.
Official population estimate totals for those aged 90 and over by sex were compared with unconstrained KT estimates and SPD estimates at the 4 time points for which data is available from all 3 sources, 9Census day 2011, mid-2013, mid-2014 and mid-2015 (Table 30).
Table 30: Comparison of official age 90 and over population estimates with Kannisto-Thatcher estimates and Statistical Population Dataset V1.0 estimates, England and Wales, 2011, 2013, 2014, 2015
| Males | Females | |||||
| KT unconstrained | Census/MYE | SPDv1 | KT unconstrained | Census/MYE | SPDv1 | |
| 2011 | 108,722 | 114,506 | 109,286 | 305,310 | 314,511 | 304,082 |
| 2013 | 123,026 | 134,797 | 127,398 | 325,479 | 343,420 | 330,165 |
| 2014 | 125,982 | 143,536 | 134,507 | 326,976 | 355,694 | 339,860 |
| 2015 | 129,977 | 148,630 | 138,627 | 327,815 | 355,400 | 338,499 |
| Source: Office for National Statistics | ||||||
| Notes: | ||||||
| 1. 2011 KTs are interpolated estimates for 31 March 2011. Esitmates for other years are for 30 June | ||||||
Download this table Table 30: Comparison of official age 90 and over population estimates with Kannisto-Thatcher estimates and Statistical Population Dataset V1.0 estimates, England and Wales, 2011, 2013, 2014, 2015
.xls (18.9 kB)Unconstrained KT estimates of the population aged 90 and over are the lowest at all time points, with the exception of 2011 for females where the unconstrained KT estimate was slightly higher than the SPD V1.0 estimate. Official estimates (Census in 2011 and MYE in 2013, 2014 and 2015) are consistently the highest, with SPD V1.0 estimates generally falling between the 2 for both males and females.
Table 31: Percentage differences between the official 90 and over population estimate and the KT estimate and the official 90 and over population estimate and the SPD V1.0 estimate, England and Wales, 2011, 2013, 2014, 2015
| Males | Females | |||
| KT | SPDv1 | KT | SPDv1 | |
| 2011 | -5.1 | -4.6 | -2.9 | -3.3 |
| 2013 | -8.7 | -5.5 | -5.2 | -3.9 |
| 2014 | -12.2 | -6.3 | -8.1 | -4.5 |
| 2015 | -12.5 | -6.7 | -7.8 | -4.8 |
| Source: Office for National Statistics | ||||
Download this table Table 31: Percentage differences between the official 90 and over population estimate and the KT estimate and the official 90 and over population estimate and the SPD V1.0 estimate, England and Wales, 2011, 2013, 2014, 2015
.xls (18.4 kB)We know that the KT method underestimates the 90 and over population for more recent years where we are furthest from cohort extinction (see Section B2). The percentage difference between the official estimate and the KT estimate generally increases over time between 2011 and 2015, which is what would be expected. There is a slight decrease for females between 2014 and 2015, which is likely to be due to a very slight reduction in the number of females aged 90 and over in 2015 compared with 2014.
The percentage difference between the SPD V1.0 estimates and the official estimate has increases by successive years (Table 31). If there is even a small over-count in the 2011 Census estimate of the 90 and over population, this will become proportionately larger over time as the estimates are rolled forward in the inter-censal years as any over-count at the oldest ages would not be removed by deaths. This could explain the observed pattern.
If there is any over-count in the 2011 Census estimate of those aged 90 and over (see Section A2) this could account for some of the differential between the 2011 KT estimate and the 2011 Census estimate and also between the 2011 SPD V1.0 estimates and the 2011 Census estimate.
b) 90 and over population by single year of age
2011 Census estimates, 2011 SPD V1.0 estimates and 2011 KT estimates for those aged 90 to age 105 and over by single year of age and sex are compared in Figures 16 and 17). Age distributions of both males and females in the 3 sources are very similar.
Figure 16: Distributions by single year of age, 90 to 105 and over , Males, 2011
England and Wales
Source: Office for National Statistics
Download this chart Figure 16: Distributions by single year of age, 90 to 105 and over , Males, 2011
Image .csv .xls
Figure 17: Distributions by singe year of age, 90 to 105 and over, Females, 2011
England and Wales
Source: Office for National Statistics
Download this chart Figure 17: Distributions by singe year of age, 90 to 105 and over, Females, 2011
Image .csv .xlsSex ratios
Sex ratios of women to men at age 90 and over by single year of age are very similar up to the age of 95 in all 3 data sources after which the ratio in the 2011 Census declines. This suggests there may be too many male centenarians in the 2011 Census or too few female centenarians (Figure 18).
Figure 18: Number of women per 100 men at ages 90 to 100 and over, 2011
England and Wales
Source: Office for National Statistics
Download this chart Figure 18: Number of women per 100 men at ages 90 to 100 and over, 2011
Image .csv .xlsFigure 19 shows percentage differences between the KT estimates and the 2011 Census estimates and between the SPD V1.0 estimates and the 2011 Census estimates for males aged 90 to 105 and over.
The SPD V1.0 estimates of males aged 90 and over by single year of age are lower than 2011 Census estimates at every age with the gap steadily increasing from age 90 to around age 99. From age 100 to 104 the pattern is more erratic, probably due to small numbers at these ages. The SPD V1.0 estimate for those aged 105 and over is noticeably lower than for the census, although again numbers at this age will be small.
Other than at ages 92 and 93, the 2011 KT estimates for males aged 90 and over by single year of age are also lower than the 2011 Census estimates at every age and although not as smooth in terms of the 2011 Census distribution, they follow a similar pattern to the SPD V1.0 estimates in terms of percentage deviations from the 2011 census estimates, including the noticeably lower estimate for the population aged 105 and over apparent in the SPD V1.0 estimates. The peak in percentage deviations of the KT estimates from the census estimate at age 92 for males is also apparent for females at age 92. This pattern is most likely due to the large increase in births in the last half of 1919 and first half of 1920 following the end of the First World War, although it is not clear why this would not also be apparent in the census and the SPD V1.0 estimates.
Figure 19: Percentage deviations of Kannisto-Thatcher and Statistical Population Dataset estimates from 2011 Census for males, ages 90 to 105 and over
England and Wales
Source: Office for National Statistics
Download this chart Figure 19: Percentage deviations of Kannisto-Thatcher and Statistical Population Dataset estimates from 2011 Census for males, ages 90 to 105 and over
Image .csv .xlsFigure 20 shows percentage differences between the KT estimates and the 2011 Census estimates and between the SPD V1.0 estimates and the 2011 Census estimates for females aged 90 to 105 and over.
The SPD V1.0 estimates of females aged 90 and over by single year of age are lower than 2011 Census estimates at every age with the gap gradually increasing from age 90 to around age 99.
Apart from the peak in deviations at ages 92 and 93, KT estimates are also lower than Census estimates up to age 99. The KT estimates are higher than the 2011 Census estimates for those aged 100 to 102 and about the same for age 103 and 104. Again the estimates of those aged 105 and over are noticeably higher in the census. The deviations of the SPD V1.0 estimates from census estimates from ages 99 to 105 and over follow the same overall pattern by single year of age as the KTs.
Figure 20: Percentage deviations of Kannisto-Thatcher and Statistical Population Dataset estimates from 2011 Census for females, ages 90 to 105 and over
England and Wales
Source: Office for National Statistics
Download this chart Figure 20: Percentage deviations of Kannisto-Thatcher and Statistical Population Dataset estimates from 2011 Census for females, ages 90 to 105 and over
Image .csv .xlsSummary and conclusions
Official estimates of the age 90 and over population are higher than SPD V1.0 estimates and SPD V1.0 estimates are generally higher than KT estimates at the 4 time points available. Age distributions of the 90 and over population in the 3 data sources are very similar.
The gap between the SPD V1.0 age 90 and over estimate total and the official age 90 and over estimate total increases by successive years of data (2011, 2013, 2014 and 2015). This could occur if there were an over-count in the 2011 Census age 90 and over estimate that is being carried forward into the inter-censal mid-year estimates and is becoming progressively proportionally larger. The improvement to the method for estimating immigration for population estimates (implemented in 2013) without a complementary change for estimating emigration may also be a contributory factor.
The sex ratio for centenarians in the 2011 Census deviates from that in the KT estimates and SPDs, suggesting that there may be too many male centenarians in the Census or too few female centenarians.
Next steps
Work is continuing to further develop the SPDs. (In May 2016 we published our first annual assessment of progress towards an Administrative Data Census post-202110 Work.) The comparisons made with SPD V1.0 illustrate the potential for using administrative data to improve high-age estimates in the future.
It should be reiterated that SPD estimates are Research Outputs and not official statistics.
Notes for Section C: Comparisons to counts derived from administrative data
- KT estimates are constrained to the official mid-year estimate of the population aged 90 and over prior to publication.
- Beyond 2011 report on autumn 2013 consultation and recommendations.
- Administrative data research outputs have been published to keep users informed of research progress and to give users the opportunity to comment on their quality. They are not official statistics.
- Research outputs estimating the size of the population in England and Wales: 2016 release
- Children aged 0-5 only need to be on the PR to be included
- Administrative Data Research Report: 2015. Methodology and Analysis of Estimates produced from a Statistical Population Dataset 2011, 2013 and 2014.
- For the purposes of comparison the estimates were not constrained to the official 90 and over population estimate totals.
- The new methodology used for SPD v2.0 led to improved counts compared to Census estimates, especially for 5- to -14-year-olds
- 2011 KT estimates are for 31 March 2011
- Administrative Data Census: Annual assessments
13. Overall summary and conclusions
Quality of the input data to high-age estimates
Deaths data
Deaths data were found to be of high quality in terms of accuracy of age at death for those dying at very high ages (105 and over) and born in England and Wales.
Deaths registration data are also complete due to the legal requirements to register a death occurring in England and Wales. However, late registrations mean that some deaths registration data for a particular year will include deaths occurring in previous years and death occurrence data will exclude deaths registered after the extraction of the annual occurrence dataset. The year-on-year numbers and distributions of death registration and death occurrence data, however, are very similar with losses and gains cancelling each other out.
It is recommended that the possibility of producing population estimates from death occurrences extracted from a live database to help increase completeness is investigated.
Census data
Overall there is a high degree of accuracy in year of birth data in the Office for National Statistics Longitudinal Study (ONS-LS) records for those aged 80 and over implying a high degree of accuracy in year of birth data for this age group in the 2011 Census as a whole.
Some discrepancies were found between 2011 Census record of year of birth and the probable “true” year of birth when looking across all available records in the ONS-LS and the proportion of cases with a discrepancy increased with age (for the 80 and over age group).
A number of potential sources of error were identified from census processes including misreporting of date of birth by either the respondent or proxy completer and scanning errors of write-in responses.
The analysis reported above suggested that the 2011 Census 90 and over estimates may be a little too high. However, it was not possible to definitively draw this conclusion as the results could be due to other factors (See Section A3).
It is recommended that findings should feed into planning for the 2021 Census, in particular the capture and quality assurance of data on the oldest old.
Migration data
The quality of UK cross-border migration data at the oldest ages appears to be reasonably good. The quality of international immigration data at the very oldest ages also appears reasonable since the method change introduced in 2013 to the mid-year population estimates (MYEs); however, emigration data at the oldest ages is likely to be of poorer quality. This in turn impacts on the quality of net migration figures at the oldest ages within MYEs.
Levels of UK cross-border migration and international migration at the oldest ages are very low. Migration, therefore, has minimal impact on the annual mid-year estimate of those aged 90 and the assumption of minimal migration in the KT method can be said to hold.
It is recommended that the impact of the change in the method for estimating emigration for the mid-year estimates is assessed.
How good is the KT method?
The Kannisto-Thatcher (KT) method was found to work well where deaths data are in the correct format and mortality rates at the oldest ages are not changing over time. Not having the input deaths data on the correct age definition has a relatively small impact on the quality of the resulting KT estimates. Where mortality rates are changing over time at the oldest ages a different method for allowing for mortality improvement may produce better estimates.
It is recommended that the possibility of obtaining deaths data by age at the beginning of the mid-year is explored to improve the quality of the KT estimates. This would also be in line with the format of data by National Records Scotland (NRS) and Northern Ireland Statistics and Research Agency (NISRA) to produce KT estimates for Scotland and Northern Ireland respectively.
It is also recommended that alternative methods for allowing for mortality improvement are investigated.
Comparisons to Research Outputs (SPD V1.0)
It was found that official population estimates of the age 90 and over population (Census and MYE) are higher than SPD V1.0 and KT estimates at the 4 time points for which comparable data was available (2011 Census day, and mid-year 2013, 2014 and 2015). Also the gap between the SPD V1.0 90 and over estimate total and the official 90 and over estimate total increases by successive years of data. This might occur if there were an over-count in the 2011 Census 90 and over estimate that is being carried forward into the inter-censal mid-year estimates and is becoming progressively proportionally larger. The change to the method for the measurement of immigration for population estimates may also be a contributory factor.
The comparisons made with SPD V1.0 illustrate the potential for using administrative data to improve high age estimates in the future.
Further research
The research and results reported in this report go some way towards evaluating the accuracy of official high-age estimates. However, there is more work that could be done.
The research and results reported in this report were presented at a workshop for external users held in March 2016. Additional topics identified for research were also presented and users were asked which of these they considered the most important to investigate, whether additional topics should be added and to help us prioritise the research going forward.
Until 2015 we produced estimates of the age 90 and over population by single year of age for England and for Wales as a whole, however, we identified a user demand for estimates for England and for Wales separately. 1Work was done to investigate whether using the KT method results in robust estimates for the 2 countries. The findings were considered by a group of internal and external methodology experts and the recommendation to produce separate estimates was accepted2. Subsequently, separate age 90 and over population estimates for England and for Wales were published on 29 September 20163.
We also publish estimates of the age 90 and over population by single year of age for the UK. These estimates are produced simply by aggregating the age 90 and over estimates calculated using the KT method for England and Wales, Scotland and Northern Ireland (produced by ourselves, National Records Scotland and Northern Ireland Statistics and Research Agency respectively). Producing these at UK level from UK level deaths data would eliminate the effects of cross-UK border migration. An assessment will be made of whether the additional work required to produce estimates by this method is justified in terms of improvement in quality.
The ONS-LS was used to look at the consistency between year of birth and age in the 2011 Census previous census records and other events data (see Section A2). There were 941 cases in the 2011 Census records of those aged 80 and over who appeared for the first time in the 2011 Census cases with no previous census records. We would expect some level of error in the ONS-LS sample. There will always be some cases where the respondent or proxy respondent has given an incorrect birth date that happens to be 1 of the 4 dates used to select the ONS-LS sample and similarly where an incorrect birthday is given that means the respondent is not selected when they should have been. The assumption is that these 2 kinds of error compensate for each other. Drawing samples from previous censuses and analysing these longitudinally, including looking at any death and embarkation records, would allow us to go some way towards testing this assumption.
The KT method requires the assumption that migration at the oldest ages is minimal. Although this assumption appears to hold (see section A3) it would be possible to model the potential impact of differing levels of migration on high-age estimates. Also, the change in methodology for estimating immigration means that we may be overstating net migration at the oldest ages in the mid-year estimates. (The previous method may have failed to account for immigration and emigration equally with little impact on overall net change.) Further work investigating ways to improve the emigration estimation at the oldest ages as a component of change in the mid-year estimates would be of value.
We could also consider further the impact of changing mortality rates over time on estimates produced by the KT method and look at different methods for allowing for these, for example, incorporating trends in the survivor ratios.
There are discontinuities in population estimates at the age 89/90 boundary where the method for calculating these changes from the cohort component method to the KT method. We could investigate these including looking at whether this is the optimum age boundary between the 2 methods.
Other research reported in the paper that we would like to expand if possible includes:
extending death data age validation to a sample of those dying from age 90 to 104 and investigating how some assessment could be made for those born outside of England and Wales
producing KT estimates for more countries with population registers to see if the pattern found in Finland and Sweden is confirmed
running the model populations using different averaging periods (k and m) for calculating the survivor ratio
Other topics we would like to work on include:
comparing our KT methodology with versions used for Human Mortality Database (HMD)
further investigate the impact of birth cohorts where births are not spread evenly over the year of birth (for example, the1918/1919/1920/1921 birth cohorts) on high-age population estimates
further work investigating the over-count in the 2001 Census/mid-year estimates of the oldest old and in the 2002 to 2010 inter-censal years
investigating producing robust age 90 and over estimates by single year of age at sub-national level
Notes for Overall summary and conclusions
- Until 2016 we pro-rated the England and Wales estimates on the basis of the 90+ totals for England and Wales to produce estimates for the separate countries needed in the production of the National Life tables.
- Feasibility of producing ‘Estimates of the very old’ for England and for Wales separately.
- Estimates of the very old (including centenarians) UK: 2002 to 2015.
