1. Overview of existing methods
In the compilation of gross domestic product (GDP), transactions involving most goods and services are valued using their market prices. Estimates of current price output are deflated using an appropriate price deflator to obtain estimates of output in constant price or volume terms.
"Non-market" services, including many public services, are not traded on a market and so we lack the prices required to deflate output. These must consequently be measured using an alternative approach. In accordance with the preferred method set out in the System of National Accounts 2008, the output of individually-consumed public services (such as education) is measured "directly", using the number of service activities provided weighted by their costs.
The Office for National Statistics (ONS) publishes two regular subnational economic output releases, which include measures of education output; these are the annual Regional Accounts and quarterly Regional GDP. These adhere to the European System of Accounts 2010 (PDF, 6.4MB) guidelines, which recommend the use of National Accounts concepts.
However, both releases have limitations in their measurement of education output. The Regional Accounts currently apportion the output of non-market education from the National Accounts to subnational areas, using the number of public sector employees in the education industry multiplied by the regional average earnings for staff in the industry. Regional GDP is benchmarked to the regional accounts; for quarters beyond the most recent regional accounts, non-market education output is apportioned subnationally, using employment data from the Inter-Departmental Business Register (IDBR).
This article assesses the feasibility of producing subnational estimates of non-market education output, using our preferred national accounts approach of cost-weighted activity, whereby the number of pupils in each school phase is weighted according to costs for each school phase. The method presented here is exploratory and the estimates we produce are experimental.
Feedback on these measures is welcome and can be sent to public.sector.outputs@ons.gov.uk.
Back to table of contents2. Data requirements
Direct volumetric output measures are calculated by weighting activities by their costs. More numerous or expensive activities consequently have a greater effect on overall output than less numerous or less expensive activities.
Formally, we use a Laspeyres index approach, which captures changes in activity while holding cost-weights constant between periods. This enables volume output growth to be measured while controlling for inflation.
Where Q is output in year t relative to year t-1, q is activity, p is unit cost, t is the year and i is activity type for n total activities.
The output of state schools in the national accounts is consequently measured using cost-weighted activity indices for each school phase. To enact this method at the subnational level, data are required at a detailed geographical level for the enrolment, attendance and costs of:
pre-primary (split by local authority (LA), and private, voluntary and independent provision)
LA-maintained primary schools
LA-maintained secondary schools
academies
special schools
The scope of this article is non-market output in the education industry, the main component of which is state schooling. Excluded from our scope are universities and further education colleges.
Back to table of contents3. Subnational enrolment and absence data
The data sources available to produce direct volume output for non-market education differ for periods before and after the onset of the coronavirus (COVID-19) pandemic, which led to widespread changes to education data collection.
Data availability prior to the coronavirus pandemic
Detailed subnational education data are available for periods prior to the coronavirus pandemic for each of the four nations of the UK; the data are available for primary, secondary and special schools, as well as academies. Data for pre-primary schools are not generally available at this level.
The level of detail in these sources varies. Data are published for Northern Ireland at the school level and for England, Scotland and Wales at the local authority (LA) level. This level of geographical detail would be sufficient for estimation at International Territorial Levels (ITLs) 1 and 2, and ITL3 with estimation for some LAs that cross ITL3 boundaries. However, as discussed further in Section 4, it is not yet possible to produce market and non-market estimates separately at ITL3. ITLs are a UK-specific replacement for the Nomenclature of territorial units for statistics (NUTS) classification and have initially been set to replicate the current NUTS breakdown.
Data available from 2020 onwards
The COVID-19 pandemic resulted in changes to education data collection. An adjustment for remote learning was also applied in the National Accounts using data on the proportion of pupils learning remotely along with a factor discounting education output. The discount factor accounted for the change in the materials covered by remote schooling and the involvement of parents and guardians in remote schooling based on a survey of teachers.
In the experimental subnational estimates, these National Accounts data are used to estimate a remote learning adjustment for each of the four nations during the period March to July 2020.
Since the autumn term of 2020, further data collections have been introduced; these enable in-school attendance to be estimated at an LA level to apply to these regional measures. Published data on in-school attendance for Scotland and Wales for this period do not split local-level attendance rates by school phase, and so the attendance data used are the same across Scotland and Wales for each school phase.
The survey used to estimate the discount factor for remote learning collects data from teachers in England only, with no equivalent survey available in the devolved administrations; English data are therefore applied across the UK. While this is a limitation for the regional estimates, the measure accounts for the timing of the restrictions requiring remote learning, this is the most important difference for output between nations and regions during the coronavirus pandemic.
Back to table of contents4. Challenges
Subnational data coverage
Data are not available at the local level for pre-primary schools, which account for around 6% of pupils nationally. In these experimental estimates, national pre-primary school output is apportioned to International Territorial Levels (ITLs) 1 and 2, using Office for National Statistics (ONS) population data on children aged two to four years. This is an imperfect apportionment, as pre-primary schooling is not compulsory and there will be geographical variation in the uptake of state-funded pre-primary school places.
Data are also not available for healthcare and teacher training provided in institutions other than universities; although as this is a small portion of total education output, these services have been excluded. As described in Section 2, the output of universities and further education colleges is also excluded.
It should be noted that as the data used for enrolments in England do not distinguish between local authority (LA)-maintained schools and academies, the unit costs for LA-maintained primary and secondary schools are applied across all primary and secondary pupils respectively. As per-pupil expenditure for LA-maintained schools and academies are not directly comparable, use of the same unit costs across both has the advantage of ensuring differences in accounting treatment between the two school types does not result in changes in output. However, this does introduce a further difference between the indices presented here and the existing treatment in the National Accounts, which considers them separately.
The academic year periodicity of the enrolment and attendance data differs from that of Regional Accounts, which is published on a calendar year basis, and regional gross domestic product (GDP), which is published quarterly. As with the National Accounts, data are estimated at the required periodicity using a cubic splining process. This process is also used for interpolating activity data for Scotland, which are collected only biennially (in even-numbered years).
While data are available to cover the current time series of Regional GDP, they are not available for Regional Accounts, which start in 1998. The experimental approach has therefore only been applied to the period 2011 onwards.
In 2015, there was a change in the definitions used in the enrolment data for England. Therefore, to avoid a break in series, data for England prior to 2015 have been re-scaled to be comparable with the later period, using growth rates for 2015 and earlier periods based on the previous definitions.
Choice of cost-weights
As described in Section 1, in the direct volume education output measure, the relative weight of different school phases in output growth is determined by their cost-weights.
Typically, secondary schools have a slightly higher cost-per-pupil than primary schools, and the cost-per-pupil of special schools is substantially greater than both primary and secondary schools.
In the National Accounts, the cost-weights used are applied to the school activity of the four UK nations, using expenditure data specific to each nation. For the regional-level estimates, three options are available:
cost-weights specific to each LA
average cost-weights for the four nations applied across the relevant nation
average cost-weights for the UK applied across the UK
The choice of cost-weights affects the growth rate and the relative level of education output in different areas. The highest-level assumption (using UK-level cost-weights) enables equivalent output to be valued equivalently across the UK; for instance, a primary school attendance would have the same effect on output were it to occur in any part of the four nations.
However, this approach would ignore the devolved nature of education provision, which enables different areas to make different funding choices. Consequently, the option of UK-level cost-weights has not been pursued.
The most detailed potential approach is to use cost-weights specific to each LA. This would result in the output varying with cost differences between LA's, including:
input costs, such as higher teacher salaries in London
pupil-to-teacher ratios, with areas with lower pupil-to-teacher ratios likely to have higher per-pupil costs
additional resources, such as for schools in deprived areas of England, through the pupil premium for children receiving free school meals
LA decisions on funding allocation
productivity, with less productive service provision likely to be associated with higher costs
However, this approach raises some conceptual challenges. LA-level output measures calculated on this basis would respond very closely to changes in local service delivery; however, by construction, they would “value” a unit of output in one part of a country or region differently to the equivalent unit in another, where costs differed.
A primary school attendance in a deprived school in London, for example, would generate apparently more output (owing to higher costs) than a primary school student in a more affluent area or outside of London. However, in "quantity" terms, the same output (one primary school attendance) has been provided.
International statistical manuals offer some guidance here, but more work remains in this area. To the extent that these differences in funding reflect differentiated output, either through the provision of additional or different services, the manuals argue that we should capture these effects in the national accounts.
However, to the extent that variation in cost-weights across space reflect differences in quality (arising from different staff-student ratios, for instance), our current National Accounts guidance states that such differences should not contribute to differences in output.
Separate measures are produced for productivity with quality adjustment incorporated. A further discussion on challenges around quantity and quality is available.
This article therefore proposes using the four-nation-level unit costs used in the National Accounts for regional estimates; this would enable funding choices at the England, Wales, Scotland and Northern Ireland level to effect school output, but not differences at the LA level. Section 4 includes a comparison of estimates produced via this approach and the LA-specific unit cost approach, and we welcome feedback on these measures.
Output, intermediate consumption and gross value added (GVA)
In the National Accounts, the direct volume output measure for education is scaled in the base year to UK government final consumption expenditure on education for the expenditure measure of GDP, and to the level of "other non-market output" for the production measure. The Regional Accounts are only compiled on the production and income basis, and not on the expenditure basis; these estimates are therefore designed to feed into the production measure.
In the production measure, overall "non-market output" includes both "other non-market output" and the small additional element of "purchases of non-market output". In these experimental estimates, "other non-market output" is calculated using the direct volume output approach, while the "purchases of non-market output" element is taken from the national accounts and apportioned to different regions in proportion to "other non-market output".
The regional accounts measure GVA, which is obtained through subtracting intermediate consumption from total output. Appropriate data for calculating intermediate consumption at the local level are not readily available. Therefore, intermediate consumption has been allocated to regions based on the ratio of intermediate consumption to total output for non-market education in the national accounts.
These experimental estimates therefore adjust the "other non-market output" that the direct volume approach is used for in the national accounts, by "purchases of non-market output" and intermediate consumption. However, as "purchases of non-market output" and intermediate consumption are apportioned based on the output obtained from the direct volume measure, they do not influence the geographical distribution of education output.
Regional level
The Regional Accounts are published at ITLs 1, 2 and 3 as well as by LA. The experimental estimates in this article are not presented at more detailed geographical levels because separate market and non-market output estimates are only processed by the less detailed ITL1 and ITL2 geographies in the Regional Accounts. Further research is needed on the split of market and non-market education estimates at the ITL3 and LA levels before our experimental estimates could be extended to this level of detail.
The data sources used in the experimental estimates generally correspond to the geographical boundaries of the ITL3 and LAs. However, in some instances, ITL3 and LA boundaries do not align.
In these cases, any further development of our experimental output estimates would need to involve an apportionment methodology to the ITL3 region. The main further limitation for ITL3 or LA breakdowns is that attendance data for Northern Ireland since 2020 are split by school phase, but not council area.
Summary of challenges, decisions and impact
In summary:
pre-primary enrolment and attendance data are not available subnationally, and so pre-primary output is apportioned by the population aged two to four years; therefore, output does not reflect local variation in pre-primary take-up rates
teacher and healthcare training data are not available subnationally, and are therefore excluded; although the effect of these services on overall output is small
a range of options for cost-weights were available with four-nation-level weights chosen, and so an additional pupil attendance by school phase will have an equivalent effect on output in any area within a nation
limited data are available for apportioning intermediate consumption, and so this is pro-rated by output; local variations in intermediate consumption therefore do not affect GVA
5. Experimental results
This section presents experimental estimates for the gross value added (GVA) of non-market education by International Territorial Level (ITL) 2. These are provided for illustrative purposes, and caution should be exercised in interpreting the results, owing to the experimental nature of these estimates (particularly with regards to differences between the four nations of the UK).
Figure 1: Gross value added from non-market education is highest in areas with the largest school-aged population
Non-market education gross value added per person by International Territorial Level 2, 2019
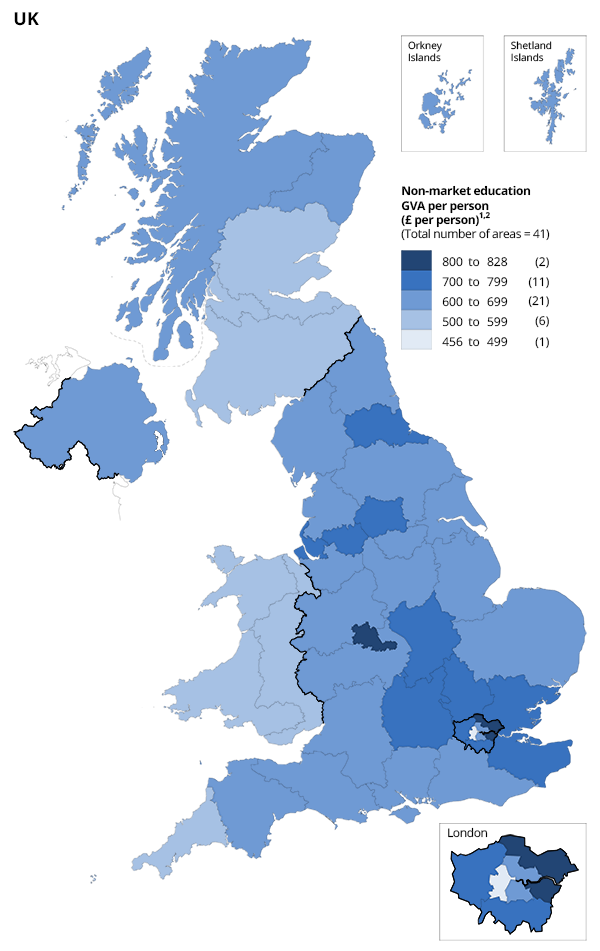
Source: Office for National Statistics - Measuring subnational education output
Download this image Figure 1: Gross value added from non-market education is highest in areas with the largest school-aged population
.png (183.3 kB) .xls (46.1 kB)Notes
Measuring subnational education output, Office for National Statistics licensed under the Open Government Licence v.3.0. Contains OS data © Crown copyright 2021. Contains LPS Intellectual Property © Crown copyright and database right (2021). This information is licensed under the terms of the Open Government Licence. Contains Open Data boundaries supplied by OSi and generalised by ONS. Graphic created by ONS Geography.
- Gross Value Added (GVA) at 2018 prices.
- International Territorial Level 2 (ITL2).
- Population estimates relate to the usual resident population.
Figure 1 shows that GVA per person from non-market education is highest in the West Midlands; this is around 80% higher than for the lowest ITL2 region, Inner London-West.
Inner London-West has an unusually low number of state school pupils, owing to its demographics and high proportion of independent school pupils. Over 30% of pupils in this region attend independent (non-state-funded) schools, which is relative to an average of around 6.5% in England.
The high GVA per person from non-market education in the West Midlands is because of a range of factors, including:
a higher-than-average school-aged population
a higher-than-average proportion of pupils in state schools
a higher-than-average proportion of pupils in special schools (the highest cost-weighted school type)
Of the factors driving differences between regions, the most important is the school-aged population, defined here as aged between 4 and 18. This is determined by both the size of the population overall and the proportion of the population that is school aged, which varies from around 15.6% to 20.0% in 2019.
Figure 2: There is limited variation in non-market education gross value added beyond that explained by school-aged population
Relationship between non-market education gross value added and school-aged population, 2019
Source: Office for National Statistics - Measuring subnational education output
Notes:
- The data is from 2019.
- The gross value added column is rounded to the nearest million.
- Where school-aged population refers to the number of 4 to 18-year-olds.
Download this chart Figure 2: There is limited variation in non-market education gross value added beyond that explained by school-aged population
Image .csv .xlsThe deviation from the 45-degree line in Figure 2 represents variation in GVA attributable to differences in:
the proportion of the school-aged population attending state schools as opposed to private schools
attendance rates
the distribution of pupils between different types of schools, such as special schools that have a higher cost-weight and therefore more GVA per pupil
unit costs between the four nations
Other than Inner London-West, a higher proportion of pupils attending independent education is a notable source of lower non-market output only in some areas of Outer London and the South East of England. Differences in the proportions of pupils in special schools are a notable source of difference between some regions because of the higher unit costs of special schools.
Attendance rates are in most cases a minor contributor to regional variation, with the highest and lowest attendance rates by ITL2 generally separated by less than 4 percentage points. However, attendance rates had a greater effect during the coronavirus (COVID-19) pandemic, particularly between devolved administrations, with some variation across the UK when teaching was predominantly remote. Data on this period are included in the reference tables.
Figure 3 provides an indication of how the adoption of the experimental method changes local-level estimates of GVA from non-market education. These figures relate to the production side of the Regional Accounts and not the headline balanced figures which weight together estimates produced on both a production and income basis and so the effect of incorporating this data into the balanced measure is likely to be smaller.
Figure 3: Some higher-cost areas see a larger downward revision in the experimental estimates
Change in non-market education gross value added from existing estimates to experimental estimates, International Territorial Level 2, 2018.
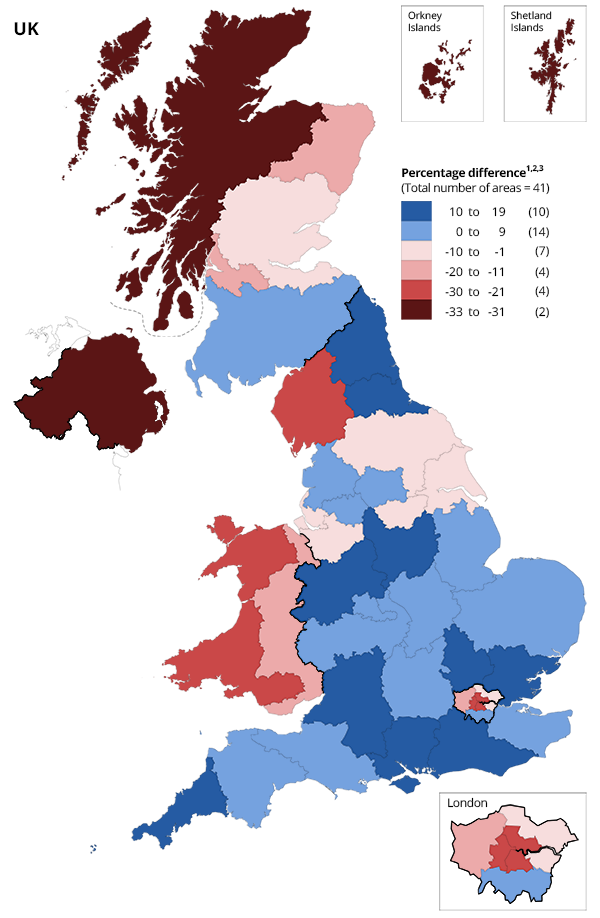
Source: Office for National Statistics - Measuring subnational education output
Download this image Figure 3: Some higher-cost areas see a larger downward revision in the experimental estimates
.png (190.3 kB) .xls (39.9 kB)Notes
Measuring subnational education output, Office for National Statistics licensed under the Open Government Licence v.3.0. Contains OS data © Crown copyright 2021. Contains LPS Intellectual Property © Crown copyright and database right (2021). This information is licensed under the terms of the Open Government Licence. Contains Open Data boundaries supplied by OSi and generalised by ONS. Graphic created by ONS Geography.
- Gross Value Added (GVA) at 2018 prices.
- International Territorial Level 2 (ITL2).
- These figures relate to the production side of the Regional Accounts.
The differences between our new measures and the existing estimates largely reflect differences between the distribution of student numbers and labour costs of education.
Some relatively rural areas, such as the Highlands and Islands, and Cumbria see a notable decrease in GVA; this may be because our experimental approach does not vary so closely with pupil-to-teacher ratios, which may be higher in rural areas.
Likewise, the experimental direct volume approach results in lower education output for London, because higher pay rates in London (which are used in our existing metrics) do not directly filter through to more output in our experimental approach.
Figure 4: Inner London and the Highlands and Islands have more education gross value added if using local-specific cost-weights
Change in non-market education gross value added from estimates based on national unit costs for each of the four nations to alternative local unit cost experimental estimates, International Territorial Level 2, 2018
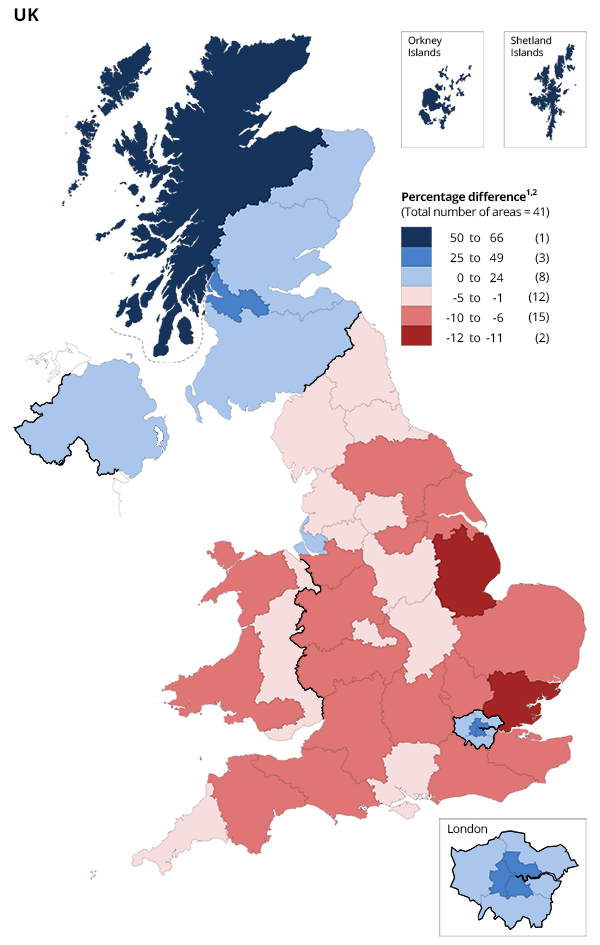
Source: Office for National Statistics - Measuring subnational education output
Download this image Figure 4: Inner London and the Highlands and Islands have more education gross value added if using local-specific cost-weights
.png (188.2 kB) .xls (44.5 kB)Notes
Measuring subnational education output, Office for National Statistics licensed under the Open Government Licence v.3.0. Contains OS data © Crown copyright 2021. Contains LPS Intellectual Property © Crown copyright and database right (2021). This information is licensed under the terms of the Open Government Licence. Contains Open Data boundaries supplied by OSi and generalised by ONS. Graphic created by ONS Geography.
- Gross Value Added (GVA) at 2018 prices.
- International Territorial Level 2 (ITL2).
As the local-specific unit cost represents differences in the expenditure per pupil, some of the pattern seen in the existing method reappears, such as the higher GVA for London and the Highlands and Islands.
It should also be noted that the local cost data sources used across the four nations are not directly comparable with the national unit costs used earlier in this section, accounting for some of the difference.
Back to table of contents6. Measuring subnational education output data
Subnational gross value added from non-market education
Dataset | Released 20 December 2021
Experimental measures of subnational gross value added from non-market education. Estimates are provided for illustrative purposes only and caution should be exercised in interpreting the results.
7. Data sources
England:
Scotland:
Wales:
Northern Ireland:
Back to table of contents8. Future developments
The experimental estimates in this article are produced using the recommended approach for non-market output in the national accounts. This article highlights several data limitations and conceptual challenges, and proposes estimation approaches to address these.
We welcome feedback from potential users of this data, which can be sent to public.sector.outputs@ons.gov.uk.
Back to table of contents