Top income adjustment in effects of taxes and benefits data: methodology

• This article concludes two years of joint research with the Department for Work and Pensions to explore new methods of addressing under coverage of the highest incomes in household finance surveys, thereby improving our understanding of trends and levels of income inequality in the UK.

• The methods explored in this research involve replacing survey responses for the richest respondents in the Living Costs and Food Survey – the principal source for ONS’ income inequality statistics - with information from a sample of administrative tax records produced by HM Revenue and Customs, known as the Survey of Personal Incomes.

• The introduction of a top income adjustment increases estimates of income inequality by an average of 1.9 percentage points over the period covering financial year ending 2002 to financial year ending 2018.

• The adjustments allow for new analyses of income inequality, for example the income share of the richest 1% of people, which has remained fairly stable at around 7% since financial year ending 2010.

• The introduction of a top income adjustment increases the coherence of estimates of levels of income inequality reported by ONS and DWP, while the trends seen in both series remain comparable. 

• The ONS will introduce its new income adjustment for the income inequality statistics for the financial year ending 2019 (to be published 5 March 2020) and create an adjusted time series going back to the financial year ending 2002.

The Office for National Statistics (ONS) and its predecessors have published statistics on the distribution and redistribution of household income since 1961. This began with 'The incidence of taxes and social service benefits', which was one of the first publications in the world to give such a complete examination of these issues.

The primary source of data for the ONS's official statistics on household income inequality is the Living Costs and Food Survey (LCF), a sample survey of private households in the UK, collecting detailed data on household income and expenditure and currently covering approximately 5,000 households. The household income dataset produced from the LCF is often known as the effects of taxes and benefits (ETB) data.

While household surveys have several important advantages over relying solely on administrative records, there is a well-recognised challenge: they do not fully capture the incomes of the richest individuals and households, particularly those among the so-called "top 1%". There are several potential reasons for this (see, for example, Lustig, 2018), the relative importance of which varies across countries and across surveys depending on the methods used. These include:

• frame or non-coverage error, where the frame used to select the sample for the survey does not fully cover the population of interest (in this case, households in the UK)

• unit non-response error, which may occur if individuals or households with higher incomes are less likely to participate in surveys than those in the rest of the income distribution

• item non-response error, if those with higher incomes participating in surveys do not report all their sources of income

• under-reporting, where the levels of income received for some sources may be intentionally or unintentionally under-reported by survey respondents

• sparseness, where data on top incomes are limited because there are fewer observations within the dataset with very high incomes, making it difficult to estimate the true distribution

This article examines the nature and scale of under-coverage of top incomes in ONS statistics on income inequality derived from the LCF. It then explores different approaches to dealing with these issues, in particular focussing on methods developed first by the Department for Work and Pensions (DWP) (2015) and then by Burkhauser et al. (2018); these make use of the Survey of Personal Incomes (SPI), a microdata set containing taxable incomes based on a sample of administrative records from UK tax payers. Building on this research, this article contrasts two top income adjustment approaches, exploring their relative impacts on headline measures of income inequality published by the ONS.

We can make an assessment of the accuracy with which the Living Costs and Food Survey (LCF) data capture personal income by comparing it to the Survey of Personal Incomes (SPI), an individual-level dataset produced from tax records by HM Revenue and Customs (HMRC), based on a sample of individuals potentially liable for UK tax.

Examining the three most recent years where full SPI datasets are available, Figure 1 highlights that at around the 97th percentile, average personal income as reported in the SPI is higher than that reported in effects of taxes and benefits (ETB) statistics. This shows that survey under-coverage is an issue for ETB statistics, and therefore measured estimates of income inequality are potentially lower than they should be.

That the ratio becomes close to 1.0 below the top few percentiles of the distribution suggests that the greatest challenge affecting top incomes in UK survey data is that of under-reporting by survey respondents rather than lower survey participation. If the primary issue was that of unit non-response, it might be expected that the ratio would remain above 1.0 considerably further down, owing to the misalignment of the two distributions resulting from those with the highest incomes being absent from the survey.

Economic research has employed a variety of methods to address the issues outlined in the previous section. While a more detailed taxonomy is provided in Lustig (2018), broadly speaking, these can be divided into three groups:

• methods that use survey data only
• those using tax data only
• those that combine survey and administrative data

Recognising our role as producers of official statistics, our approach needs to be methodologically robust, based on academic research and existing best practice, as well as being transparent and understandable by users. In addition, the value of effects of taxes and benefits (ETB) microdata to academics and researchers needs to be reflected, with any approach continuing to enable the replication of headline measures using the data. This means the method needs to be applied to the underlying microdata rather than to the headline measures themselves.

The adjusted data should also permit the reporting of income on a household, rather than individual, basis reflecting the greater insight this measure provides because of, for example, intrahousehold sharing of resources. Finally, the selected approach needs to be feasible considering the current availability of source data.

This final reason leads us away from approaches that rely on the direct use of linked survey and administrative data at this stage of the research. In the longer term, this is our ambition as more record-level administrative data become available within the Office for National Statistics (ONS) under the Digital Economy Act 2017. This will help to improve the quality of estimates of income both at the bottom and top of the income distribution while maintaining the detailed information about people and households (such as intrahousehold relationships, spending and health status) that is not so readily available in administrative data. However, there still remains a clear need to develop and introduce a method of bringing together the survey and administrative data that does not rely on direct record linkage, that can be applied now, and that allows for the production of historical data.

These criteria have led us to the set of methods first implemented in the UK by the Department for Work and Pensions (DWP) for the households below average incomes (HBAI) statistics, which are based on the Family Resources Survey (FRS). This method, often referred to as the "SPI adjustment" owing to its use of HM Revenue and Customs' (HMRC's) Survey of Personal Incomes (SPI) data, involves replacing the incomes of the richest 0.32% and 1.16% of working-age people and pensioners, respectively, with cell-mean imputations based on corresponding observations in tax return data. The SPI adjustment also stratifies separately for Great Britain and Northern Ireland.

The groundbreaking work of the original SPI adjustment is recognised by Burkhauser et al. (2018), but they argue that with the increasing interest in income inequality and the income shares of specific groups such as the so-called "top 1%", the SPI approach requires "new scrutiny". They outline several recommendations for optimising the SPI adjustment, setting out a so-called "SPI2" methodology.

First, they demonstrate that survey under-coverage of top incomes in HBAI data tends to become more of an issue from around the 95th percentile upwards, becoming particularly acute from the top 2%. As highlighted in Figure 1, similar results are demonstrated in ETB data, making a case for adjusting incomes at a lower threshold than that currently set by the SPI1 adjustment.

Burkhauser et al. also compare the ratios of adjusted HBAI data with SPI data at different quantile groups towards the top of the distribution. They highlight that the gap between the mean incomes of HBAI and SPI quantile groups is reduced for the top 2% to 1% group as well as for the top 1% to 0.5% group. However, they further highlight that the correspondence between adjusted-HBAI data and SPI data remains low towards the very top of the distribution (in the top 0.5% to 0.1% group and the top 0.1%). They argue that this stems from the fact that cell means from the original SPI adjustment are calculated from a wide range of incomes. Therefore, the adjustment tends to impute incomes that are too low for the 0.5 to 0.1 percentile group and too small for the top 0.1%. They conclude that more granular adjustments could lead to improved measures of income inequality for the top incomes.

Aside from applying a lower threshold and increased granularity, the SPI2 adjustment differs in two important ways from the original SPI methodology. First, the SPI2 methodology contains no stratification for pensioner and non-pensioner individuals or for Great Britain and Northern Ireland. Secondly, the SPI2 does not involve reweighting of the data, instead simply replacing survey incomes for each quantile group with the SPI mean for the same quantile group.

This paper therefore builds on the work of both the DWP and Burkhauser et al., through exploring different methodological choices with the aim of identifying a perceived optimum variant for use with the ONS's household income statistics, considering the various constraints that exist.

In determining the optimal approach to adjust for under-coverage of top incomes in effects of taxes and benefits (ETB) statistics, two underlying methods are used and tested. The first, which we term the "quantile" approach, closely resembles the so-called "SPI2 approach" developed by Burkhauser et al. The second - "reweighting" - brings together elements of both the SPI2 and the original Survey of Personal Incomes (SPI) adjustment adopted for households below average income (HBAI) statistics.

Under the quantile approach, the mean gross income for each SPI quantile group is imputed onto individuals in the equivalent quantile groups in the survey data. More specifically:

1. estimate personal taxable income for individuals on ETB data

2. add a dummy case to the SPI data to account for individuals who do not pay tax; their personal taxable income is set to zero, and their weight reflects the difference in population totals between the ETB and SPI datasets

3. rank individuals in ETB and SPI data by personal taxable income

4. allocate individuals at the top of both the ETB and SPI distributions to quantile groups, depending on the threshold and granularity selected (for example, at the 97th percentile and 0.5% levels of granularity, there will be six groups of individuals at the top, each representing 0.5% of the population)

5. calculate the mean personal taxable income for each quantile group in the SPI data

6. replace the income of each case within the ETB quantile groups with the mean SPI income from the corresponding group

7. add back several income components to the ETB cases not represented in SPI data, such as individual savings accounts (ISAs) and intrahousehold transfers

8. re-calculate Income Tax and National Insurance contributions for the adjusted ETB cases based on new estimates of personal pre-tax income

9. aggregate personal-level income across household members to estimate adjusted household disposable income

By contrast, the reweighting methodology replaces steps four to six with the following:

4a. allocate individuals at the top of the SPI distributions to quantile groups, depending on the threshold and granularity selected (for example, at the 97th percentile and 0.5% levels of granularity, there will be six groups of individuals at the top, each representing 0.5% of the population)

4b. calculate the lower income boundaries for each of these quantile groups on the SPI data and create bands in the ETB data using these boundaries

5. calculate the mean personal taxable income for each quantile group in the SPI data and impute this onto individuals in the equivalent survey bands

6a. reweight the ETB bands so that their weights are the same as the SPI quantiles

6b. reweight the unadjusted ETB data so that overall population totals for each weighting variable are maintained

Where the primary challenge affecting top incomes is that of under-reporting rather than lower survey participation of the richest households, the effects of the two methods should be largely equivalent in practice. However, where lower participation also has a significant impact, the second "reweighting" method should prove more effective.

The combination of two different SPI adjustment methods (reweighting and quantile), many possibilities in both the threshold and granularity of adjustments, as well as the decision on whether to adjust pensioners and non-pensioners separately means that there are many choices to be made in selecting a preferred approach. In determining this, we have sought to address the following questions:

• Should the richest pensioners and non-pensioners be adjusted separately?
• How low should the threshold be?
• How granular should the adjustment be?
• Should the quantile or reweighting method be chosen?
• Should estimates be revised once final outturn data are available?

Recommendation to adjust richest pensioners and non-pensioners separately

The SPI adjustment currently implemented in HBAI statistics involves separately adjusting the income of the richest pensioners and non-pensioners. Considering this approach, Burkhauser et al. (2018) question whether there is a clear rationale for doing so. Exploring these issues in more detail, Figure 2 presents the ratio of average (mean) personal taxable income by quantile group reported on ETB and SPI data, for both pensioner and non-pensioner distributions.

The ratio of taxable income measured on ETB and SPI data for working-age people closely resembles the whole population average shown in Figure 1, hovering around 1.0 before sharply increasing at the 96th percentile. We see a similar observation in the distribution of pensioners, where the ratio also increases at the 96th percentile. In contrast with the non-pensioner distribution, the ratio remains above 1.0 during the entirety of the portion of the distribution shown in this chart, suggesting that the income distribution for pensioners is affected by both under-reporting and unit non-response.

These findings confirm that survey under-coverage of top incomes affects both the non-pensioner and pensioner distributions. Only 1.7% of pensioners have a personal taxable income high enough to feature in the top 5% of the overall income distribution. This means that an adjustment applied just to the overall distribution would be unlikely to fully adjust for under-coverage of the incomes of pensioners. Given this is an important breakdown in the analysis produced by the Office for National Statistics (ONS), there is a clear rationale for stratifying by pensioner and non-pensioner, as is currently done by the Department for Work and Pensions (DWP).

Recommended income threshold for adjustments

In considering the threshold to use, there is a balance that needs to be struck. Too high, and there is a risk that the adjustment does not fully account for survey under-coverage. Too low, and survey data are being unnecessarily discarded in exchange for averages from the SPI.

As demonstrated in Figure 1, under-coverage of top incomes in the Living Costs and Food Survey (LCF) becomes an issue at around the 96th percentile. On this evidence, thresholds ranging from the 95th to 99th percentile are explored and tested, using both the quantile and reweighting methods. In testing these different thresholds, the quantile group sizes were held constant at 0.5%.

Over the period considered, differences between the various adjustments, based on different thresholds, are relatively small, under both the quantile and reweighting methods. By far the largest difference is that between having any adjustment and not having one at all.

For instance, Figure 3 looks at the mean of the richest 10% (Figure 3), across the 5 adjustments, and over the period financial year ending 2002 to financial year ending 2018. It shows that under the quantile method, the average absolute deviation of the five adjustments from their mean is 0.4%, compared with the 14.2% average difference between each adjusted estimate and the unadjusted amount. Similarly, under the reweighting approach, these figures are 0.5% and 16.2% respectively.

The same is also true when examining the Gini coefficient (Figure 4). Under the quantile method, the average absolute deviation of the 5 adjustments from their mean is 0.1 percentage points, compared with the 1.8 percentage point average absolute difference between each adjusted estimate and the unadjusted amount. Similarly, under the reweighting approach, these figures are 0.1 and 2.0 percentage points respectively. 

The gap between the adjusted and unadjusted is greatest during the period between the financial year ending 2006 and the financial year ending 2010 where, according the reweighting method, the average income of the richest 10% increased by 28.5% between the financial year ending 2002 and the financial year ending 2008, before falling 20.8% by the financial year ending 2013. This compares with the unadjusted data, which were much more stable over this period.

Figure 3: The mean of the richest 10% across the five adjustments

Mean equivalized household disposable income of the richest 10% of people, with varying thresholds, 0.5% granularity, UK, financial year ending 2002 to financial year ending 2018

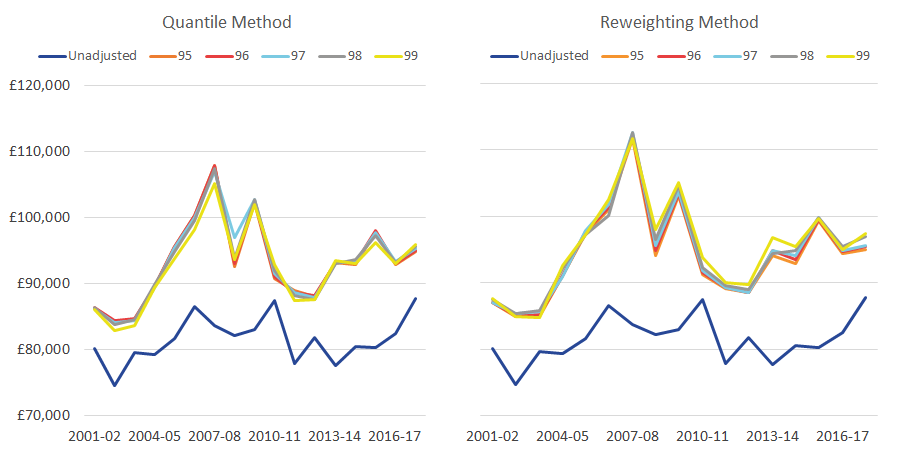
Source: Office for National Statistics – Living Costs and Food Survey; HM Revenue and Customs – Survey of Personal Incomes

Download this image Figure 3: The mean of the richest 10% across the five adjustments

.png (55.2 kB) .xlsx (18.4 kB)

The trends of adjusted data compared with unadjusted data over time are broadly similar. The most notable exception is during the four years from the financial year ending 2006, where income inequality increases sharply as measured using adjusted data, before falling back to similar levels observed in the unadjusted data. Also, between the financial year ending 2013 and the financial year ending 2016, there is a larger rise in inequality in the adjusted data compared with the unadjusted data. However, the gap between adjusted and unadjusted data narrows between the financial year ending 2016 and the financial year ending 2018 because of a larger rise in the inequality in the unadjusted data.

In the financial year ending 2011, there is little difference between the Gini coefficients for the adjusted and unadjusted data. This most likely reflects the introduction of a 50% top tax rate in the financial year ending 2011, with evidence to suggest that this led to people forestalling their income (HM Revenue and Customs (HMRC), 2012), which has resulted in the tax data for top earners being not as different to the survey data in the financial year ending 2011 as they are in other years.

Figure 4: The Gini coefficient at varying thresholds

Gini coefficient of disposable income, with varying thresholds, 0.5% granularity, UK, financial year ending 2002 to financial year ending 2018

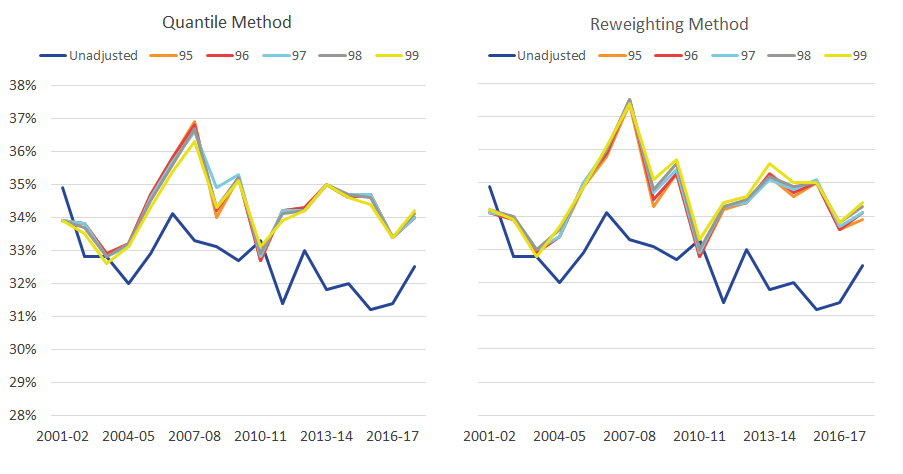
Source: Office for National Statistics – Living Costs and Food Survey; HM Revenue and Customs – Survey of Personal Incomes

Download this image Figure 4: The Gini coefficient at varying thresholds

.png (60.2 kB) .xlsx (20.6 kB)

Looking across the time series, the threshold that is the furthest away from the average of the adjustments is the 99th percentile threshold. Suggesting that the 99th percentile threshold may not fully address the survey under-coverage (though, these differences are very small in comparison to the difference between having an adjustment and not).

Recommended quantile band size

Another consideration when applying a methodology for adjusting top incomes is the width of quantile bands. While smaller quantile groups may provide more granularity to the adjusted data - potentially allowing for a closer representation of the upper tail of the income distribution - we risk finding ourselves with very few, maybe zero, cases within bands in the survey data. However, this can only be found under the reweighting approach. By construction, there will always be cases on the survey data when bands are formed on the basis of quantiles, as is the case under the quantile approach, rather than the income thresholds used for the reweighting approach.

Whichever quantile group size is used, the top-income adjustment has a similar effect on both the average income of the richest 10% (Figure 5) and the Gini coefficient (Figure 6). In both cases, the differences between adjustments are much smaller than any differences between adjusted and unadjusted data (excluding the financial year ending 2011, as discussed earlier).

Across all years, the average change in income of the richest 10%, compared with the unadjusted data, is 14.5% for the quantile method and 15.9% for the reweighting method (Figure 5). The different trends in the adjusted and unadjusted data, in the income of the richest 10% over time, are broadly similar to those discussed in the recommended income threshold for adjustments.

While the differences between adjustments based on different quantile bands are small under the quantile method, they are slightly more pronounced under the reweighting method. For example, while the average absolute difference between adjustments based on 0.25% and 1.0% quantile bands is 0.6% under the quantile method, it is 0.8% using the reweighting approach.

Figure 5: Whichever quantile group size is used, the top-income adjustment has a similar effect on the average income of the richest 10%

Mean equivalised household disposable income of the richest 10%, with varying granularities, 97th threshold, UK, financial year ending 2002 to financial year ending 2018

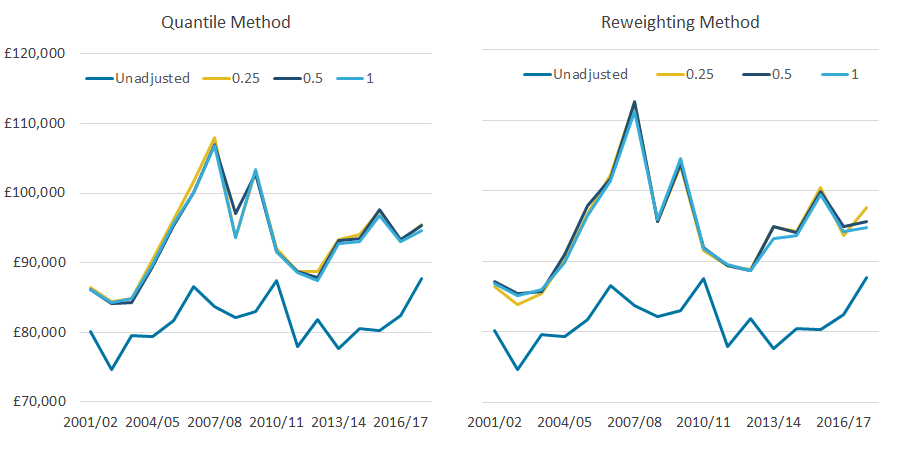
Source: Office for National Statistics – Living Costs and Food Survey; HM Revenue and Customs – Survey of Personal Incomes

Download this image Figure 5: Whichever quantile group size is used, the top-income adjustment has a similar effect on the average income of the richest 10%

.png (49.9 kB) .xlsx (19.4 kB)

Looking at the Gini coefficient, over the period analysed, the average difference between the unadjusted and adjusted data is 1.7 and 1.9 percentage points for the quantile and reweighting methods respectively. The differences between the different quantile sizes is considerably smaller. The difference between the 1.0% and 0.25% quantile bands in the reweighting approach is not so pronounced when measuring the Gini coefficient, compared with measures for the average income of the top 10%.

Figure 6: Whichever quantile group size is used, the top-income adjustment has a similar effect on the Gini coefficient

Gini coefficient of disposable income with varying granularities, 97th percentile threshold, UK, financial year ending 2002 to financial year ending 2018

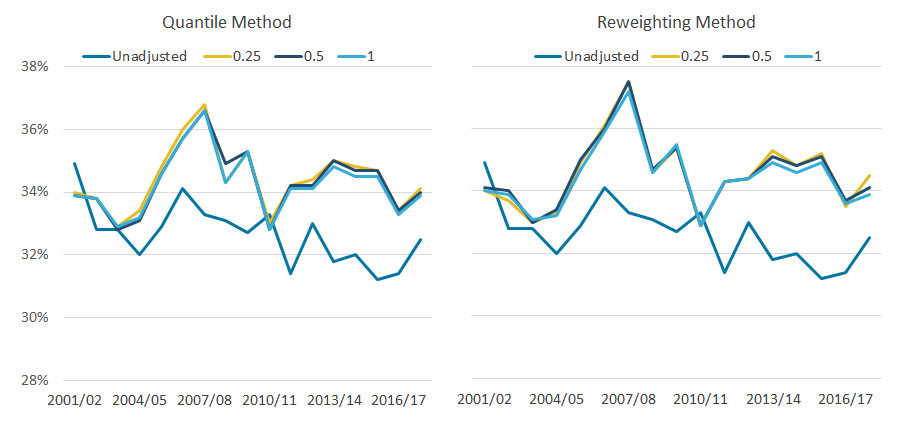
Source: Office for National Statistics – Living Costs and Food Survey; HM Revenue and Customs – Survey of Personal Incomes

Download this image Figure 6: Whichever quantile group size is used, the top-income adjustment has a similar effect on the Gini coefficient

.png (48.2 kB) .xlsx (19.4 kB)

Income share of the top 1%

While the impact of changing the granularity is modest on estimates of income of the richest 10% and the Gini coefficient, there are much more substantial differences between quantile band sizes when examining the top 1% of individuals.

Figure 7 highlights that estimates for the income share of the top 1% are slightly higher with a 0.25% quantile band size, compared with 0.5%, which in turn gives considerably higher estimates in most years than 1.0%. For example when using the reweighting method, the average share of income for the top 1% is 6.1% between the financial year ending 2011 and the financial year ending 2018, based on quantile band sizes of 1.0%, compared with 5.1% when the data are unadjusted. This average increases to 7.1% and 7.7% for 0.5% and 0.25% quantile band sizes respectively.

Figure 7: Estimates for the income share of the top 1% are slightly higher with a 0.25% quantile band size, compared with 0.5%

Share of household equivalised disposable income received by the richest 1% of individuals, with varying granularities, 97th threshold, UK, financial year ending 2002 to financial year ending 2018

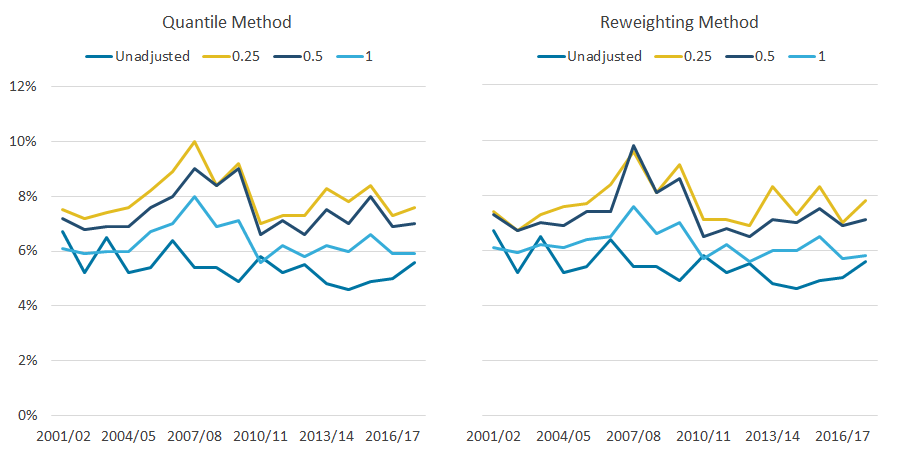
Source: Office for National Statistics – Living Costs and Food Survey; HM Revenue and Customs – Survey of Personal Incomes

Download this image Figure 7: Estimates for the income share of the top 1% are slightly higher with a 0.25% quantile band size, compared with 0.5%

.png (41.1 kB) .xlsx (19.5 kB)

These differences arise as a result of the composition of households at the top of the distribution. This reflects that most households have multiple occupants, but typically only one person will have a personal income high enough to warrant being adjusted. For instance, in the 2017 to 2018 dataset, just under half of the people in the top 1% of people based on personal income are in the top 1% based on household income. This means that most of those in the top 1% of household income, using a 0.25% quantile band size adjustment, will contain those whose incomes have been replaced with an average of the 0.5% richest people as reported in the SPI. Whereas, people in the top 1% of household income, adjusted using 1.0% quantile band sizes, will include people who have had their income replaced with the lower mean derived from the top 1% of the SPI data, and hence they have a lower estimated income share.

Given the increasing focus on measures such as the income share of the top 1%, these findings suggest that 1.0% quantile bands are too broad. However, the trade-off when applying the reweighting method is the increasing likelihood of empty bands on the survey data for smaller quantile band sizes, resulting in adjusted survey data that are not as representative of the tax data. For example, in the hypothetical situation where the richest three 0.25% bands of pensioners are empty, adjusted data will not reflect the average income of the richest 0.75% of pensioners, resulting in less precise measures of income inequality and greater volatility at the top of the distribution.

From the financial year ending 2002 to the financial year ending 2018, only 7 out of 340 bands were empty. This highlights that while the issue of empty bands can occur, it is not at a scale considered large enough to be considered a major issue. Therefore, adjustments based on 0.25% quantile bands are most likely to be optimal, with the greater granularity offered ensuring a more realistic approximation of the upper tail of the income distribution.

Recommendations on quantile and reweighting methods

The analysis presented so far highlights that while estimates of the Gini coefficient (using a 97 percentile threshold and quantile band sizes of 0.25%) were broadly similar since the financial year ending 2012, the Gini coefficient under the reweighting approach has been marginally higher than for the quantile approach.

Figure 1 suggested that the primary reason for the under-coverage of top incomes in the LCF was under-reporting rather than unit non-response. However, if that were entirely the case, it might be expected that the quantile and re-weighting approaches would be almost identical. That the Gini coefficient is marginally higher under the reweighting approach suggests that non-response at the top of the distribution does play some role. This indicates that although more complex, the reweighting approach is preferred.

Another reason for adopting the reweighting approach comes from Figure 2, which highlighted that, although non-response may be a lesser concern for the overall income distribution (mirroring the findings of Burkhauser et al.), there is evidence to suggest it may be more noticeable in the distribution of pensioners' incomes.

A further important consideration is coherence. The reweighting approach is closest in methodological terms to the SPI adjustment currently used by the DWP's HBAI statistics. Adopting this approach therefore ensures coherence in terms of methods across the UK Government Statistical Service (GSS).

Recommendation on whether estimates should be revised once final outturn data are available

One of the challenges in implementing the approaches discussed in this paper is their reliance on SPI data, which are not typically made available to researchers until at least two years after the end of the income reference period. Therefore, it is necessary to use estimates provided by HMRC, which are based on projections from historical SPI datasets. This raises the question of whether to revise the measures of Gini coefficients once the final SPI data become available.

To address these questions, we compare estimates of inequality based on projected and outturn data. In this analysis, we used projected SPI estimates that were originally supplied to the DWP in the production of their HBAI statistics to adjust ETB statistics. These results were then compared to estimates using the same adjustment but using final outturn data that had since been published.

The analysis in Figure 9 demonstrates that the impact of moving from projected to final data leads to, on average, a 0.2 percentage points revision of the Gini coefficient. Given that the 95% confidence intervals of published Gini coefficients are usually wider than even the largest observed revision, these results do not provide a compelling case for revising measures of Gini coefficients once final SPI data are made available at this stage. Therefore, we do not propose a policy of regular revision to our household income statistics, following the adoption of the new top-income adjustment, to take account of the outturn SPI data when they become available. However, this will need to be closely monitored, initially once the financial year ending 2018 SPI data are released later in 2020 and for a few years thereafter to determine whether this revision policy needs re-evaluating.

The analysis presented in this article confirms that survey under-coverage of top incomes in effects of taxes and benefits (ETB) data is an issue, but it is one that is addressed by employing methods that adjust the income of the highest earners with information provided by administrative tax records. We have demonstrated that the optimum approach to use is the reweighting approach, which stratifies by pensioners and non-pensioners at the 97th percentile threshold and in 0.25% quantile groups.

We plan to introduce this adjustment in income distritbutions statistics covering 2018 onwards, to be published in March 2020. At this stage, the adjusted ETB time series will go back to the financial year ending 2002, reflecting the availability of Survey of Personal Incomes (SPI) data from the UK Data Service (UKDS). However, we intend to explore options for extending the time series back further, ideally to 1977, reflecting the start of the ETB data currently available. We will also make the top income-adjusted ETB statistics available to researchers via the UKDS.

Burkhauser RV, Hérault N, Jenkins SP and Wilkins R (2018), ‘Top incomes and inequality in the UK: reconciling estimates from household Survey and tax return data’, Oxford Economic Paper, Volume 70, Issue 2, pages 301 to 326.

Burkhauser RV, Hérault N, Jenkins SP and Wilkins R (2018a), ‘Survey under-coverage of top incomes and estimation of inequality: what is the role of the UK’s SPI adjustment?’, Fiscal Studies, Volume 39, Issue 2, pages 213 to 240.

Department of Work and Pensions (2015). Households below average income: an analysis of the income distribution 1994/95 to 2013/14, London: Department for Work and Pensions.

Her Majesty’s Revenue and Customs (2012), ‘The Exchequer effect of the 50 per cent additional rate of income tax’, The National Archives.

Lustig N (2018), ‘Measuring the distribution of household income, consumption and wealth’, in Stiglitz JE, Fitoussi J-P and Durand M (editors), For Good Measure: Advancing Research on Well-being Metrics Beyond GDP, Paris: Organisation for Economic Co-operation and Development Publishing.

Richard Tonkin, Dominic Webber, Ozer Beha, Martin Shine, and Callum Clark, Office for National Statistics. With thanks to Peter Matejic (Department for Work and Pensions), Stephen Jenkins (London School of Economics), Steve Martin-Drury (Office for National Statistics), and the Survey Personal Incomes statistical team (Her Majesty’s Revenue and Customs) for their incredibly helpful input throughout the development of this work to date.